在上一篇博客中,提到了对似然函数的理解,由给定样本推导出参数。
定义
这里记录一下 似然函数的数学定义(连续型随机变量的)
设X是连续型随机变量,![]() 是多维参数向量,是模型的参数。概率密度函数为
是多维参数向量,是模型的参数。概率密度函数为![]() 。
。![]() 是从总体中采样得到的样本,
是从总体中采样得到的样本,![]() 独立同分布,那么联合概率密度为:
独立同分布,那么联合概率密度为:
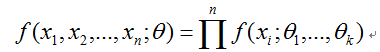
由于![]() 是已知的,而参数
是已知的,而参数![]() 是未知的,上式的联合概率密度可以看成是
是未知的,上式的联合概率密度可以看成是![]() 的函数。记为
的函数。记为

称之为似然函数。
似然函数值 的大小意味着样本组的值出现的可能性大小,求参数θ的值,使用得似然函数取最大值,这种方法就是最大似然估计
理解:
1、在实践中,由于求导数的需要,往往将似然函数取对数,得到对数似然函数;若对数似然函数可导,可能过求导的方式,解方程组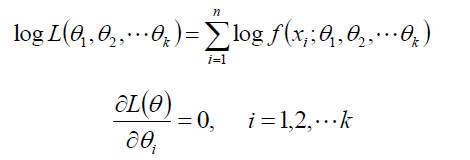
得到驻点,然后分析该驻点是极大值的点
2、最大似然估计 找出与样本的分布最接近的概率分布模型
求解步骤






















 979
979

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








