1318. Logarithm
Time Limit: 1.0 second
Memory Limit: 16 MB
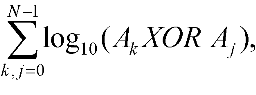
Input
Output
Sample
| input | output |
|---|---|
| 2 0 0 0 2324 0 2332 0 0 | 44 |
Problem Source: VIII Collegiate Students Urals Programming Contest. Yekaterinburg, March 11-16, 2004
解答如下(只保留 Main 方法):
{
UInt128[] numbers = UInt128.Read(Console.In);
int v = 0 ;
for ( int i = 0 ; i < numbers.Length - 1 ; i ++ )
for ( int j = i + 1 ; j < numbers.Length; j ++ )
v += UInt128.Log10(UInt128.Xor(numbers[i], numbers[j]));
Console.WriteLine(v * 2 );
}
这个程序的算法是非常直接了当的。程序中用到了 BigInteger 类,其源代码在 浅谈 BigInteger 这篇随笔中。
因为 2128 ≈ 3.4 x 1038,所以在程序中使用一个数组来存储 100, 101, ... 1038 各个数(程序中第 28 行)。在计算对数时,即程序中第 80 行开始的 Log10 方法中,使用二分搜索法在该数组中查找就行了。
这道题目限时是 1.0 秒。问题是我的这个程序运行时会超时,无法 Accept。我想不出来还有什么更快的方法了。谁可以告诉我更好的算法?
(以下是 2009-03-17 补充的,并于 2009-03-19 修改)
根据本文5楼的评论,参阅了数学研发论坛上的“关于一个运算优化的问题”的贴子,终于把这题通过了。
根据本文12楼的评论,修改后的程序的运行时间是 0.218 秒。
首先,根据该贴子,我们有以下定理:
如果 log 210 n < log 2X < log 210 n+1 并且 log 2Y < log 2X, 则:log 10(X xor Y) = n上面定理中的所有对数的值都要取整。实际上,log2X 就表示 X 的二进制位数。同样,log10X 就表示 X 的十进制位数。
利用上面的定理,就可以用分治法来解这道题。
还是先看看 C# 源程序吧:
2 using System.IO;
3
4 namespace Skyiv.Ben.Timus
5 {
6 // http://acm.timus.ru/problem.aspx?space=1 &num=1318
7 sealed class T1318
8 {
9 static void Main()
10 {
11 var p = UInt128.Read(Console.In);
12 Array.Sort(p);
13 Console.WriteLine( 2 * Solve(p, 127 , 0 , p.Length - 1 ));
14 }
15
16 static int Solve(UInt128[] p, int bit, int low, int high)
17 {
18 if (bit < 3 || low >= high) return 0 ;
19 var mid = BinarySearch(p, bit, low, high);
20 var v = Solve(p, bit, low, high, mid);
21 v += Solve(p, bit - 1 , low, mid - 1 );
22 v += Solve(p, bit - 1 , mid, high);
23 return v;
24 }
25
26 static int Solve(UInt128[] p, int bit, int low, int high, int mid)
27 {
28 if (low >= mid || mid > high) return 0 ;
29 var n = UInt128.Log10s[bit];
30 if (n >= 0 ) return n * (mid - low) * (high - mid + 1 );
31 return Solve(p, bit - 1 , - n, low, mid - 1 , mid, high);
32 }
33
34 static int Solve(UInt128[] p, int bit, int n, int low0, int high0, int low1, int high1)
35 {
36 if (bit < 3 || low0 > high0 || low1 > high1) return 0 ;
37 var mid0 = BinarySearch(p, bit, low0, high0);
38 var mid1 = BinarySearch(p, bit, low1, high1);
39 if (UInt128.Powers[n].IsSetBit(bit)) return
40 ((mid0 - low0) * (mid1 - low1) + (high0 + 1 - mid0) * (high1 + 1 - mid1)) * (n - 1 ) +
41 Solve(p, bit - 1 , n, low0, mid0 - 1 , mid1, high1) +
42 Solve(p, bit - 1 , n, mid0, high0, low1, mid1 - 1 );
43 else return
44 ((mid0 - low0) * (high1 + 1 - mid1) + (high0 + 1 - mid0) * (mid1 - low1)) * n +
45 Solve(p, bit - 1 , n, low0, mid0 - 1 , low1, mid1 - 1 ) +
46 Solve(p, bit - 1 , n, mid0, high0, mid1, high1);
47 }
48
49 static int BinarySearch(UInt128[] p, int bit, int low, int high)
50 {
51 var isSet = false ;
52 int mid = 0 , i = low, j = high;
53 while (i <= j)
54 if (isSet = p[mid = (i + j) / 2 ].IsSetBit(bit)) j = mid - 1 ;
55 else i = mid + 1 ;
56 return isSet ? mid : (mid + 1 );
57 }
58 }
59
60 sealed class UInt128 : IComparable < UInt128 >
61 {
62 public static readonly UInt128[] Powers = new UInt128[ 39 ]; // 存放 10 的 0, 1,
 , 38 次幂
, 38 次幂
63 public static readonly int [] Log10s = new int [ 128 ]; // 值域为: [-38, 38]
64 uint [] data;
65
66 static UInt128()
67 {
68 var log2s = new int [Powers.Length];
69 BigInteger p32 = BigInteger.Pow( 2 , 32 ), p64 = p32 * p32, p96 = p64 * p32, q = 1 ;
70 for (var i = 0 ; i < Powers.Length; i ++ , q *= 10 )
71 {
72 BigInteger r;
73 var u0 = uint .Parse(BigInteger.DivRem(q, p96, out r).ToString());
74 var u1 = uint .Parse(BigInteger.DivRem(r, p64, out r).ToString());
75 var u2 = uint .Parse(BigInteger.DivRem(r, p32, out r).ToString());
76 Powers[i] = new UInt128( uint .Parse(r.ToString()), u2, u1, u0);
77 log2s[i] = Powers[i].Log2();
78 }
79 for ( int i = 1 , j = 0 ; i < Log10s.Length; i ++ )
80 {
81 if (j < log2s.Length - 1 && i == log2s[j + 1 ]) j ++ ;
82 Log10s[i] = (i == log2s[j]) ? - j : j;
83 }
84 }
85
86 UInt128( params uint [] data)
87 {
88 this .data = new uint [ 128 / 32 ];
89 for ( int i = data.Length - 1 ; i >= 0 ; i -- ) this .data[i] = data[i];
90 }
91
92 static UInt128 FromInt32s( string s)
93 {
94 var u = s.Split();
95 return new UInt128( uint .Parse(u[ 3 ]), uint .Parse(u[ 2 ]), uint .Parse(u[ 1 ]), uint .Parse(u[ 0 ]));
96 }
97
98 public int CompareTo(UInt128 other)
99 {
100 if (data[ 3 ] > other.data[ 3 ]) return 1 ;
101 if (data[ 3 ] < other.data[ 3 ]) return - 1 ;
102 if (data[ 2 ] > other.data[ 2 ]) return 1 ;
103 if (data[ 2 ] < other.data[ 2 ]) return - 1 ;
104 if (data[ 1 ] > other.data[ 1 ]) return 1 ;
105 if (data[ 1 ] < other.data[ 1 ]) return - 1 ;
106 if (data[ 0 ] > other.data[ 0 ]) return 1 ;
107 if (data[ 0 ] < other.data[ 0 ]) return - 1 ;
108 return 0 ;
109 }
110
111 public static UInt128[] Read(TextReader reader)
112 {
113 var p = new UInt128[ int .Parse(reader.ReadLine())];
114 for (var i = p.Length - 1 ; i >= 0 ; i -- ) p[i] = UInt128.FromInt32s(reader.ReadLine());
115 return p;
116 }
117
118 int Log2()
119 {
120 int [] bs = { 0 , 32 , 64 , 96 };
121 for (var i = 3 ; i >= 0 ; i -- )
122 {
123 var u = data[i];
124 if (u == 0 ) continue ;
125 for (var bit = 31 ; bit >= 0 ; bit -- , u <<= 1 )
126 if (( ~ int .MaxValue & u) != 0 ) return bit + bs[i];
127 }
128 return - 1 ;
129 }
130
131 public bool IsSetBit( int bit)
132 {
133 return ((data[bit / 32 ] >> (bit % 32 )) & 1 ) != 0 ;
134 }
135 }
136 }
程序中,Main 方法位于第 9 到 14 行。第 11 行读取输入到一个 UInt128 数组中。第 12 行将该数组排序。第 13 行调用 Solve 方法进行分治法递归计算来解题。其中传入的参数 127 表示从 UInt128 的最高位开始,逐步往低位计算。
在第 16 到 24 行的 Solve 方法中,第 19 行的 mid 指示数组 p 的首个使第 bit 位为 1 的元素。这样,根据 mid 就把数组 p 的元素分为两组,第 20 行调用第二个 Solve 方法处理这两组之间的元素。第 21 和 22 行递归调用 Solve 自身分别处理这两组内的元素。
在第 26 到 32 行的第二个 Solve 方法中,如果发现这两组元素满足上面定理的条件,则在第 30 行直接将计算结果返回。否则,就在第 31 行调用第三个 Solve 方法来处理。
在第 34 到 47 行的第三个 Solve 方法中,继续根据低一位的第 bit 位再把这两组元素分别分为两组。这四组元素之间异或后的对数值不是 n 就是 n - 1。这时根据 10n 的二进制表示法中第 bit 位来判断是哪种情况。其中有两组可以直接得到结果,另外两组就递归地调用自身来处理。
实际上这整个程序都没有进行过 Xor 和 Log10 运算,而是不断通过分组进行处理。
第 60 到 136 行就是 UInt128 类。
第 62 行的 powers 静态数组存放 100, 101, ..., 1038。
第 63 行的 Log10s 静态数组存放的是 log102n,其中 n 从 0 到 127。这个数组的意思是指定的二进制位的数所对应的十进制数有几位,并且该位数第一个出现时对应的数组元素取负值。这个数组在程序的第 29 行用来判断是否满足上述定理的条件。
第 64 行的 data 数组使用 4 个 UInt32 来表示 UInt128。
第 66 到 84 行的静态构造函数用来初始化以上两个静态数组。
UInt128 类的其它方法也都很简单,就不多说了。
(以下是 2009-03-26 补充的)
这个程序还可以优化,即事先计算出静态数组 Powers 和 Log10s 的值,不使用 BigInteger 类。将递归中没有改变的参数 p 外提为类的字段。如下所示:
2 using System.IO;
3
4 namespace Skyiv.Ben.Timus
5 {
6 // http://acm.timus.ru/problem.aspx?space=1 &num=1318
7 sealed class T1318
8 {
9 static UInt128[] p;
10 static int n;
11
12 static void Main()
13 {
14 Array.Sort(p = UInt128.Read(Console.In));
15 Console.WriteLine( 2 * Solve( 127 , 0 , p.Length - 1 ));
16 }
17
18 static int Solve( int bit, int low, int high)
19 {
20 if (bit < 3 || low >= high) return 0 ;
21 var mid = BinarySearch(bit, low, high);
22 return Solve(bit, low, high, mid) +
23 Solve(bit - 1 , low, mid - 1 ) +
24 Solve(bit - 1 , mid, high);
25 }
26
27 static int Solve( int bit, int low, int high, int mid)
28 {
29 if (low >= mid || mid > high) return 0 ;
30 n = UInt128.Log10s[bit];
31 if (n >= 0 ) return n * (mid - low) * (high - mid + 1 );
32 n = - n;
33 return Solve(bit - 1 , low, mid - 1 , mid, high);
34 }
35
36 static int Solve( int bit, int low0, int high0, int low1, int high1)
37 {
38 if (bit < 3 || low0 > high0 || low1 > high1) return 0 ;
39 var mid0 = BinarySearch(bit, low0, high0);
40 var mid1 = BinarySearch(bit, low1, high1);
41 return UInt128.Powers[n].IsSetBit(bit) ?
42 (((mid0 - low0) * (mid1 - low1) + (high0 + 1 - mid0) * (high1 + 1 - mid1)) * (n - 1 ) +
43 Solve(bit - 1 , low0, mid0 - 1 , mid1, high1) +
44 Solve(bit - 1 , mid0, high0, low1, mid1 - 1 )) :
45 (((mid0 - low0) * (high1 + 1 - mid1) + (high0 + 1 - mid0) * (mid1 - low1)) * n +
46 Solve(bit - 1 , low0, mid0 - 1 , low1, mid1 - 1 ) +
47 Solve(bit - 1 , mid0, high0, mid1, high1));
48 }
49
50 static int BinarySearch( int bit, int low, int high)
51 {
52 var isSet = false ;
53 int mid = 0 , i = low, j = high;
54 while (i <= j)
55 if (isSet = p[mid = (i + j) / 2 ].IsSetBit(bit)) j = mid - 1 ;
56 else i = mid + 1 ;
57 return isSet ? mid : (mid + 1 );
58 }
59 }
60
61 sealed class UInt128 : IComparable < UInt128 >
62 {
63 public static readonly UInt128[] Powers =
64 {
65 new UInt128( 1 , 0 , 0 , 0 ),
66 new UInt128( 10 , 0 , 0 , 0 ),
67 new UInt128( 100 , 0 , 0 , 0 ),
68 new UInt128( 1000 , 0 , 0 , 0 ),
69 new UInt128( 10000 , 0 , 0 , 0 ),
70 new UInt128( 100000 , 0 , 0 , 0 ),
71 new UInt128( 1000000 , 0 , 0 , 0 ),
72 new UInt128( 10000000 , 0 , 0 , 0 ),
73 new UInt128( 100000000 , 0 , 0 , 0 ),
74 new UInt128( 1000000000 , 0 , 0 , 0 ),
75 new UInt128( 1410065408 , 2 , 0 , 0 ),
76 new UInt128( 1215752192 , 23 , 0 , 0 ),
77 new UInt128( 3567587328 , 232 , 0 , 0 ),
78 new UInt128( 1316134912 , 2328 , 0 , 0 ),
79 new UInt128( 276447232 , 23283 , 0 , 0 ),
80 new UInt128( 2764472320 , 232830 , 0 , 0 ),
81 new UInt128( 1874919424 , 2328306 , 0 , 0 ),
82 new UInt128( 1569325056 , 23283064 , 0 , 0 ),
83 new UInt128( 2808348672 , 232830643 , 0 , 0 ),
84 new UInt128( 2313682944 , 2328306436 , 0 , 0 ),
85 new UInt128( 1661992960 , 1808227885 , 5 , 0 ),
86 new UInt128( 3735027712 , 902409669 , 54 , 0 ),
87 new UInt128( 2990538752 , 434162106 , 542 , 0 ),
88 new UInt128( 4135583744 , 46653770 , 5421 , 0 ),
89 new UInt128( 2701131776 , 466537709 , 54210 , 0 ),
90 new UInt128( 1241513984 , 370409800 , 542101 , 0 ),
91 new UInt128( 3825205248 , 3704098002 , 5421010 , 0 ),
92 new UInt128( 3892314112 , 2681241660 , 54210108 , 0 ),
93 new UInt128( 268435456 , 1042612833 , 542101086 , 0 ),
94 new UInt128( 2684354560 , 1836193738 , 1126043566 , 1 ),
95 new UInt128( 1073741824 , 1182068202 , 2670501072 , 12 ),
96 new UInt128( 2147483648 , 3230747430 , 935206946 , 126 ),
97 new UInt128( 0 , 2242703233 , 762134875 , 1262 ),
98 new UInt128( 0 , 952195850 , 3326381459 , 12621 ),
99 new UInt128( 0 , 932023908 , 3199043520 , 126217 ),
100 new UInt128( 0 , 730304488 , 1925664130 , 1262177 ),
101 new UInt128( 0 , 3008077584 , 2076772117 , 12621774 ),
102 new UInt128( 0 , 16004768 , 3587851993 , 126217744 ),
103 new UInt128( 0 , 160047680 , 1518781562 , 1262177448 )
104 };
105 public static readonly int [] Log10s =
106 {
107 0 , 0 , 0 , - 1 , 1 , 1 , - 2 , 2 , 2 , - 3 , 3 , 3 , 3 , - 4 , 4 , 4 , - 5 , 5 , 5 , - 6 , 6 , 6 , 6 , - 7 , 7 , 7 ,
108 - 8 , 8 , 8 , - 9 , 9 , 9 , 9 , - 10 , 10 , 10 , - 11 , 11 , 11 , - 12 , 12 , 12 , 12 , - 13 , 13 , 13 ,
109 - 14 , 14 , 14 , - 15 , 15 , 15 , 15 , - 16 , 16 , 16 , - 17 , 17 , 17 , - 18 , 18 , 18 , 18 ,
110 - 19 , 19 , 19 , - 20 , 20 , 20 , - 21 , 21 , 21 , 21 , - 22 , 22 , 22 , - 23 , 23 , 23 ,
111 - 24 , 24 , 24 , 24 , - 25 , 25 , 25 , - 26 , 26 , 26 , - 27 , 27 , 27 , 27 , - 28 , 28 , 28 ,
112 - 29 , 29 , 29 , - 30 , 30 , 30 , - 31 , 31 , 31 , 31 , - 32 , 32 , 32 , - 33 , 33 , 33 ,
113 - 34 , 34 , 34 , 34 , - 35 , 35 , 35 , - 36 , 36 , 36 , - 37 , 37 , 37 , 37 , - 38 , 38
114 };
115 uint [] data;
116
117 UInt128( params uint [] data)
118 {
119 this .data = new uint [ 128 / 32 ];
120 for ( int i = data.Length - 1 ; i >= 0 ; i -- ) this .data[i] = data[i];
121 }
122
123 public int CompareTo(UInt128 other)
124 {
125 if (data[ 3 ] > other.data[ 3 ]) return 1 ;
126 if (data[ 3 ] < other.data[ 3 ]) return - 1 ;
127 if (data[ 2 ] > other.data[ 2 ]) return 1 ;
128 if (data[ 2 ] < other.data[ 2 ]) return - 1 ;
129 if (data[ 1 ] > other.data[ 1 ]) return 1 ;
130 if (data[ 1 ] < other.data[ 1 ]) return - 1 ;
131 if (data[ 0 ] > other.data[ 0 ]) return 1 ;
132 if (data[ 0 ] < other.data[ 0 ]) return - 1 ;
133 return 0 ;
134 }
135
136 public bool IsSetBit( int bit)
137 {
138 return ((data[bit / 32 ] >> (bit % 32 )) & 1 ) != 0 ;
139 }
140
141 public static UInt128[] Read(TextReader reader)
142 {
143 var p = new UInt128[ int .Parse(reader.ReadLine())];
144 for (var i = p.Length - 1 ; i >= 0 ; i -- )
145 {
146 var u = reader.ReadLine().Split();
147 p[i] = new UInt128( uint .Parse(u[ 3 ]), uint .Parse(u[ 2 ]), uint .Parse(u[ 1 ]), uint .Parse(u[ 0 ]));
148 }
149 return p;
150 }
151 }
152 }
优化后程序的运行时间降低到 0.156 秒。
另外,按以下方法直接计算也是可以的,运行时间为 0.406 秒。
2 using System.IO;
3
4 namespace Skyiv.Ben.Timus
5 {
6 // http://acm.timus.ru/problem.aspx?space=1 &num=1318
7 sealed class T1318b
8 {
9 static readonly int nUInt = 128 / 32 ;
10
11 static void Main()
12 {
13 var p = Read(Console.In);
14 Console.WriteLine( 2 * Solve(p));
15 }
16
17 static uint [] Read(TextReader reader)
18 {
19 var n = int .Parse(reader.ReadLine());
20 var p = new uint [n * nUInt];
21 for (var i = 0 ; i < n; i ++ )
22 {
23 var ss = reader.ReadLine().Split();
24 for (var j = 0 ; j < nUInt; j ++ ) p[i * nUInt + j] = uint .Parse(ss[j]);
25 }
26 return p;
27 }
28
29 static int Solve( uint [] p)
30 {
31 var v = 0 ;
32 for (var i = p.Length / nUInt - 1 ; i > 0 ; i -- )
33 for (var j = i - 1 ; j >= 0 ; j -- )
34 {
35 var u = i * nUInt;
36 var y = j * nUInt;
37 var a = p[u] ^ p[y];
38 var b = p[u + 1 ] ^ p[y + 1 ];
39 var c = p[u + 2 ] ^ p[y + 2 ];
40 var d = p[u + 3 ] ^ p[y + 3 ];
41 if (a == 0 && b == 0 && c == 0 ) goto label1;
42 if (a > 1262177448 || a == 1262177448 && (b > 1518781562 || b == 1518781562 && c >= 160047680 )) { v += 38 ; continue ; }
43 if (a > 126217744 || a == 126217744 && (b > 3587851993 || b == 3587851993 && c >= 16004768 )) { v += 37 ; continue ; }
44 if (a > 12621774 || a == 12621774 && (b > 2076772117 || b == 2076772117 && c >= 3008077584 )) { v += 36 ; continue ; }
45 if (a > 1262177 || a == 1262177 && (b > 1925664130 || b == 1925664130 && c >= 730304488 )) { v += 35 ; continue ; }
46 if (a > 126217 || a == 126217 && (b > 3199043520 || b == 3199043520 && c >= 932023908 )) { v += 34 ; continue ; }
47 if (a > 12621 || a == 12621 && (b > 3326381459 || b == 3326381459 && c >= 952195850 )) { v += 33 ; continue ; }
48 if (a > 1262 || a == 1262 && (b > 762134875 || b == 762134875 && c >= 2242703233 )) { v += 32 ; continue ; }
49 if (a > 126 || a == 126 && (b > 935206946 || b == 935206946 && (c > 3230747430 || c == 3230747430 && d > 2147483647 ))) { v += 31 ; continue ; }
50 if (a > 12 || a == 12 && (b > 2670501072 || b == 2670501072 && (c > 1182068202 || c == 1182068202 && d > 1073741823 ))) { v += 30 ; continue ; }
51 if (a > 1 || a == 1 && (b > 1126043566 || b == 1126043566 && (c > 1836193738 || c == 1836193738 && d > 2684354559 ))) { v += 29 ; continue ; }
52 if (a > 0 || b > 542101086 || b == 542101086 && (c > 1042612833 || c == 1042612833 && d > 268435455 )) { v += 28 ; continue ; }
53 if (b > 54210108 || b == 54210108 && (c > 2681241660 || c == 2681241660 && d > 3892314111 )) { v += 27 ; continue ; }
54 if (b > 5421010 || b == 5421010 && (c > 3704098002 || c == 3704098002 && d > 3825205247 )) { v += 26 ; continue ; }
55 if (b > 542101 || b == 542101 && (c > 370409800 || c == 370409800 && d > 1241513983 )) { v += 25 ; continue ; }
56 if (b > 54210 || b == 54210 && (c > 466537709 || c == 466537709 && d > 2701131775 )) { v += 24 ; continue ; }
57 if (b > 5421 || b == 5421 && (c > 46653770 || c == 46653770 && d > 4135583743 )) { v += 23 ; continue ; }
58 if (b > 542 || b == 542 && (c > 434162106 || c == 434162106 && d > 2990538751 )) { v += 22 ; continue ; }
59 if (b > 54 || b == 54 && (c > 902409669 || c == 902409669 && d > 3735027711 )) { v += 21 ; continue ; }
60 if (b > 5 || b == 5 && (c > 1808227885 || c == 1808227885 && d > 1661992959 )) { v += 20 ; continue ; }
61 if (b > 0 || c > 2328306436 || c == 2328306436 && d > 2328306435 ) { v += 19 ; continue ; }
62 if (c > 232830643 || c == 232830643 && d > 2808348671 ) { v += 18 ; continue ; }
63 if (c > 23283064 || c == 23283064 && d > 1569325055 ) { v += 17 ; continue ; }
64 if (c > 2328306 || c == 2328306 && d > 1874919423 ) { v += 16 ; continue ; }
65 if (c > 232830 || c == 232830 && d > 2764472319 ) { v += 15 ; continue ; }
66 if (c > 23283 || c == 23283 && d > 276447231 ) { v += 14 ; continue ; }
67 if (c > 2328 || c == 2328 && d > 1316134911 ) { v += 13 ; continue ; }
68 if (c > 232 || c == 232 && d > 3567587327 ) { v += 12 ; continue ; }
69 if (c > 23 || c == 23 && d > 1215752191 ) { v += 11 ; continue ; }
70 if (c > 2 || c == 2 && d > 1410065407 ) { v += 10 ; continue ; }
71 label1:
72 if (c > 0 || d > 999999999 ) { v += 9 ; continue ; }
73 if (d > 99999999 ) { v += 8 ; continue ; }
74 if (d > 9999999 ) { v += 7 ; continue ; }
75 if (d > 999999 ) { v += 6 ; continue ; }
76 if (d > 99999 ) { v += 5 ; continue ; }
77 if (d > 9999 ) { v += 4 ; continue ; }
78 if (d > 999 ) { v += 3 ; continue ; }
79 if (d > 99 ) { v += 2 ; continue ; }
80 if (d > 9 ) { v ++ ; continue ; }
81 }
82 return v;
83 }
84 }
85 }
返回目录







 本文详细解析Timus1318.Logarithm问题的算法实现过程,针对128-bit数进行XOR运算后取对数求和的挑战,介绍了高效的分治法解决方案及直接计算法。
本文详细解析Timus1318.Logarithm问题的算法实现过程,针对128-bit数进行XOR运算后取对数求和的挑战,介绍了高效的分治法解决方案及直接计算法。

















 1985
1985

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








