二叉树的构建

最新推荐文章于 2025-12-20 10:32:27 发布

转载最新推荐文章于 2025-12-20 10:32:27 发布 · 84 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/nigang/p/3564877.html

文章标签：

#数据结构与算法

本文详细介绍了如何使用C++语言构建一个简单的二叉树，包括节点定义、构造函数实现及树的构建过程。

二叉树（Binary Tree）是将数据按一定的分支关系组织起来的结构，保存数据的基本节点（Node）最多有两个子树，通常子树的根被称之为“左子树”（Left subtree）和“右子树”（Right subtree）。

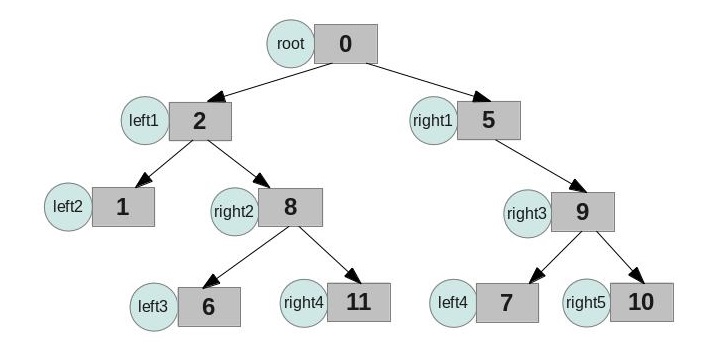
图1 一个简单的二叉树

由二叉树的性质可知，一个节点最基本的三要素为：保存节点的值以及指向左右子树的指针。

1 typedef struct binTree{
2     int data;
3     struct binTree* left;
4     struct binTree* right;
5 }BinNode, *BinTree;

View Code

构造如图1所示的二叉树，如下代码。

 1 /*
 2  *                     root
 3  *            left1               right1
 4  *     left2       right2                right3
 5  *            left3     right4     left4        right5
 6  */
 7 
 8 void createBinTree(BinTree& root){
 9     BinTree left1 = new BinNode;
10     BinTree right1 = new BinNode;
11     left1->data = 2;
12     right1->data = 5;
13     root->left = left1;
14     root->right = right1;    //Construct the first layer.
15 
16     BinTree left2 = new BinNode;
17     BinTree right2 = new BinNode;
18     left2->data = 1;
19     right2->data = 8;
20     left1->left = left2;
21     left1->right = right2;
22     BinTree right3 = new BinNode;
23     right3->data = 9;
24     right1->right = right3;        //Construct the second layer
25 
26     BinTree left3 = new BinNode;
27     left3->data = 6;
28     right2->left = left3;
29     BinTree right4 = new BinNode;
30     right4->data = 11;
31     right2->right = right4;
32 
33     BinTree left4 = new BinNode;
34     left4->data = 7;
35     right3->left = left4;
36     BinTree right5 = new BinNode;
37     right5->data = 10;
38     right3->right = right5;
39 }

View Code

完整代码：

 1 #include<iostream>
 2 using namespace std;
 3 
 4 typedef struct binTree{
 5     int data;
 6     struct binTree* left;
 7     struct binTree* right;
 8 }BinNode, *BinTree;
 9 
10 /*
11  *                     root
12  *            left1               right1
13  *     left2       right2                right3
14  *            left3     right4     left4        right5
15  */
16 
17 void createBinTree(BinTree& root){
18     BinTree left1 = new BinNode;
19     BinTree right1 = new BinNode;
20     left1->data = 2;
21     right1->data = 5;
22     root->left = left1;
23     root->right = right1;    //Construct the first layer.
24 
25     BinTree left2 = new BinNode;
26     BinTree right2 = new BinNode;
27     left2->data = 1;
28     right2->data = 8;
29     left1->left = left2;
30     left1->right = right2;
31     BinTree right3 = new BinNode;
32     right3->data = 9;
33     right1->right = right3;        //Construct the second layer
34 
35     BinTree left3 = new BinNode;
36     left3->data = 6;
37     right2->left = left3;
38     BinTree right4 = new BinNode;
39     right4->data = 11;
40     right2->right = right4;
41 
42     BinTree left4 = new BinNode;
43     left4->data = 7;
44     right3->left = left4;
45     BinTree right5 = new BinNode;
46     right5->data = 10;
47     right3->right = right5;
48 }
49 
50 int main(void){
51     BinTree  root = new BinNode;
52     root->data = 0;
53     createBinTree(root);
54         return 0;
55 }