把正方形映射为圆

2019独角兽企业重金招聘Python工程师标准>>>

把正方形映射为圆

翻译自:Mapping a Square to a Circle

• 全部机器翻译, 看看能不能读

I wanted to come up with a nice way to map all the points in the square

我想以一种精密的方式来映射一个正方形中的所有点.

截图1: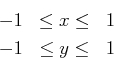

to the points in the unit circle, such that the points along the axes are unchanged, and the corners get normalized. The way I went about this was to think of a line of constant x (as well as a line of constant y) getting mapped to an ellipse in the circle. So for our first requirement to hold true, the ellipse for some constant x has the equation

对于单位圆中的点来说, 沿着坐标轴的那些点是不变的, 角被归一化了. 在这方面我的办法是认为行的恒定 x （以及不断 y 线） 获取映射到椭圆的圈子。所以我们举行真正的第一要求，一些常量 x 椭圆有方程

截图2:

Now we want to make sure that points along the curve at the top of the circle (from 45 degrees to 135 degrees) are all accounted for. So for x between -1 and 1, we want the ellipse to pass through the point

现在我们想要确保，点沿曲线顶部的圈子 （从 45 度到 135 度） 都占。所以 x-1 和 1 之间，我们想要通过点的椭圆

截图3:

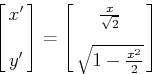
So we'll plug that in, and that should give us the b coefficient for our ellipse

所以我们将它打开，和那应该给我们为我们的椭圆的 b 系数

截图4:

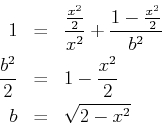
So the ellipse for constant x is

所以为常数 x 椭圆

截图5:

Similarly, for a line of constant y, we get the ellipse

同样，对于恒定 y 的线条，我们得到椭圆

截图6:

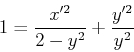
Solving the first for x', we get

解决第一个为 x'，我们得到

截图7:

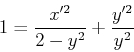
Plugging this into the second equation gives

这插入第二个方程给出了

截图8:

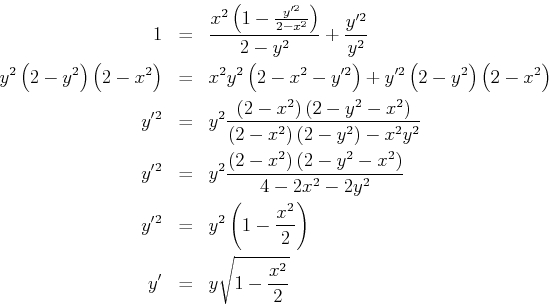
and by symmetry we can see that the mapping

由对称性，我们可以看到，映射

截图9:

takes the square from -1 to 1 on the x and y axes, to the unit circle. Here's a demonstration of that mapping, which shows its effect on various grid lines.

以广场从-1 到 1 的 x 和 y 轴，到单位圆。这里是示范该映射，显示其对各种网格线的影响。

截图10:

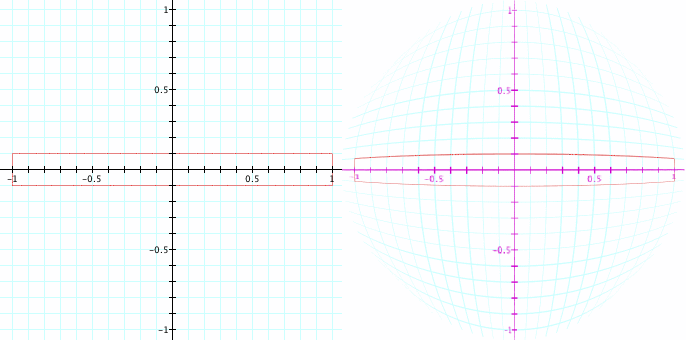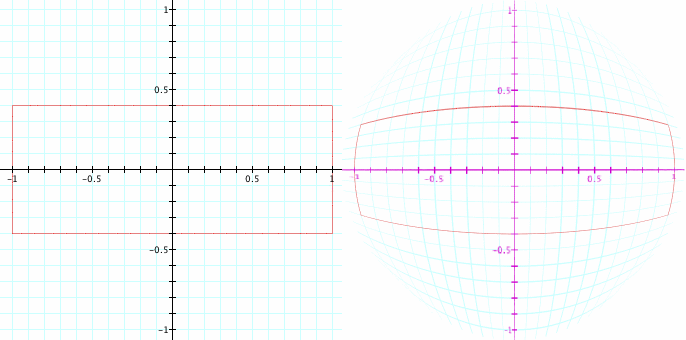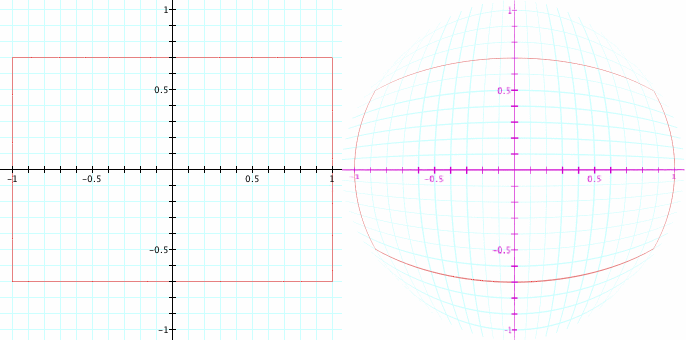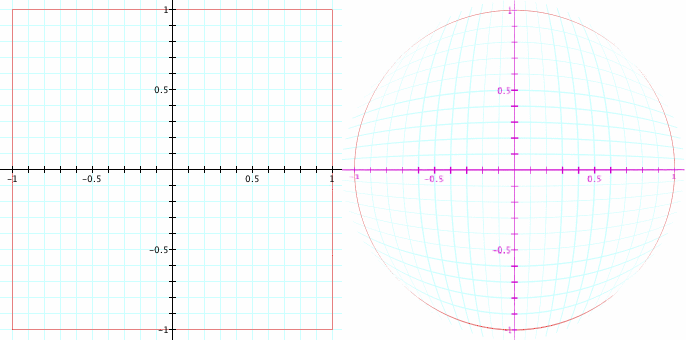
I'd like to find a way to map a cube to the unit sphere. Hopefully I can get that ready for the next post.

我想找到某种映射到单位球面的多维数据集。但愿我能，准备接下来的文章。

转载于:https://my.oschina.net/freeblues/blog/715850