小孩上楼梯的方式的种类

2019独角兽企业重金招聘Python工程师标准>>>

 

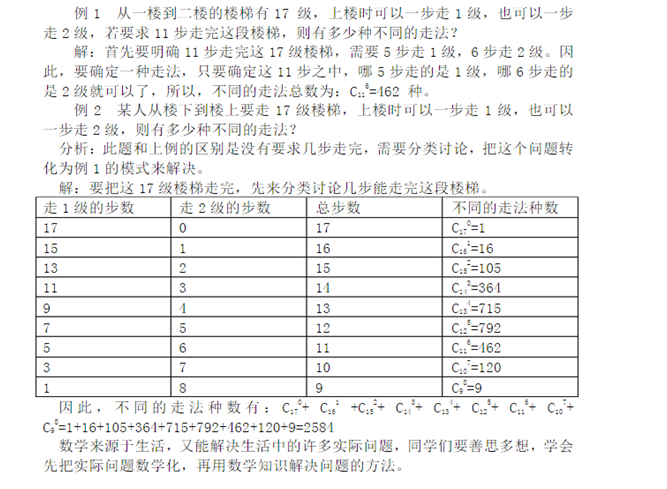
例3：一共有10级,每次可走一步也可以走两步.必须要8步走完10级楼梯. 问:一共有多少种走法?

分析：走一步的需要6次，走两步的需要2次。因此，本题是6个1、2个2的组合问题。在6个一步中，插入2个两步的,因可放在第一个1步之前,也可以放在最后一个1步之后,所以6个1步有7个空.因此,如果两个两步在一起有c(7,1)种;如果两个两步的分开来插有C(7，2）种，因此共有

    c(7,1)+c(7,2)=7+21=28(种)=C(8,2)=C（8,6） 

    总数=8步中选2中走两步的=8步中选6个走一步的

 

Java编程实现：（数组迭代，动态规划，递归）

package com.test;

public classzoutaijie {

// 梯有N阶，上楼可以一步上一阶，也可以一次上二阶。编一个程序，计算共有多少种不同的走法。如果上20阶会有几种走法

public staticlongresult[]=new long[100];

public staticvoidmain(String[] args) {

result[0]=result[1]=1;

for(inti=2;i<</span>result.length;i++)

result[i]=-1;

//s不能太大，否则int溢出

int s =60;

//动态规划

long startTime = System.currentTimeMillis();

System.out.println("动态规划解决："+fun1(s));

long endTime = System.currentTimeMillis();

System.out.println("动态规划解决-程序运行时间："+(endTime-startTime)+"ms");

 

//数组叠加

long startTime2 = System.currentTimeMillis();

System.out.println("数组叠加实现："+fun2(s));

long endTime2 = System.currentTimeMillis();

System.out.println("数组叠加实现-程序运行时间："+(endTime2-startTime2)+"ms");

 

//递归方法

long startTime1 = System.currentTimeMillis();

System.out.println("递归方法解决："+fun(s));

long endTime1 = System.currentTimeMillis();

System.out.println("递归方法解决-程序运行时间："+(endTime1-startTime1)+"ms");

}

 

 

 

public staticlongfun(ints){

if(s==0 || s==1)

return 1;

else{

return fun(s-1)+fun(s-2);

}

 

}

 

public staticlongfun1(ints){

if(result[s]>=0) {

return result[s];

}else{

result[s]=(fun1(s-1)+fun1(s-2));

return result[s];

}

}

 

 

public staticlongfun2(ints){

long result_1[]=newlong[s+1];//注意这个要大一个，多了个第0个

result_1[0]=result_1[1]=1;

for(inti=2;i<=s;i++)

result_1[i]=result_1[i-1]+result_1[i-2];

return result_1[s];//s就是第s+1个

}

 

}

 

 

 

分析:

  （1） int s=48时候的运行效果：

 

 

 

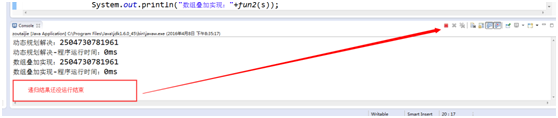
（2）. int s=60时候的运行效果

 

 

 

  显然数组叠加和动态规划效率高很多很多，不是一个数量级的！

 

 

/**

 * 功能：有个小孩正在上楼梯，楼梯有n阶台阶，小孩一次可以上1阶、2阶或3阶。计算小孩上楼梯的方式有多少种。

 */

 

三种方法：

 

方法一:

//递归法
	/**
	 * 思路：自上而下的方式。
	 * 最后一步可能是从第n-1阶往上走1阶、从第n-2阶往上走2阶或从第n-3阶往上走3阶。
	 * 因此，抵达最后一阶的走法，抵达这最后三阶的方式的综合。
	 * @param n
	 * @return
	 */
	public static int countWays(int n){
		if(n<0)
			return 0;
		else if(n==0)//注意此处条件
			return 1;
		else{
			return countWays(n-1)+countWays(n-2)+countWays(n-3);
		}
	}

 

方法二：

//动态规划
	/**
	 * 思路：每次调用都会分支出三次调用。予以动态规划加以修正。
	 * @param n
	 * @param map
	 * @return
	 */
	public static int countWaysDP(int n,int[] map){
		if(n<0)
			return 0;
		else if(n==0)
			return 1;
		else if(map[n]>-1)
			return map[n];
		else{
			map[n]=countWaysDP(n-1,map)+countWaysDP(n-2,map)+countWaysDP(n-3, map);
			return map[n];
		}
	}

 

方法三：

1. package com.tian;
2.  
3. import java.util.TreeMap;
4.  
5. /**
6. * 爬楼梯的算法(有一个人要爬楼梯，楼梯有N个台阶，此人最多可以爬M个台阶
7. * 问这个人上楼有多少中上法)
8. * @author Administrator
9. *
10. */
11. public class Test {
12.  
13.  
14.  
15. public static void main(String[] args) {
16. System.out.println(new Test().suanfa(3,1));
17. }
18.  
19. /**
20. * 得到所有能相加等于这个数的2个非自然正数
21. * @param n
22. */
23. public void fenjie(final int n){
24.  
25. for (int i = 1; i <=n; i++) {
26.  
27.  
28. System.out.println(i+","+(n-i));
29. }
30. }
31.  
32. /**
33. *
34. * @param n 总台阶数
35. * @param m 最多能走的步数
36. * @return 返回能走方法数
37. */
38. public int suanfa(final int n,final int m){
39.  
40. switch (n) {
41. case 1:
42. return 1;
43.  
44. case 2:
45. if(m>=2){
46. return 2;
47. }
48. else{
49. return 1;
50. }
51. }
52. int result=0;
53. for (int i = 1; i <n; i++) {
54. int a=i;
55. int b=n-i;
56.  
57. System.out.println(i+","+(n-i));
58. result+=suanfa(a, m)*suanfa(b, m);
59. }
60. return result;
61.  
62.  
63.  
64. }
65. }

转载于:https://my.oschina.net/u/2822116/blog/791822