并行计算奇异值分解--Jacobi旋转

最新推荐文章于 2025-06-28 09:15:21 发布

转载最新推荐文章于 2025-06-28 09:15:21 发布 · 1.1k 阅读

文章标签：

介绍SVD奇异值分解的原理及应用，详细讲解基于Jacobi旋转法的SVD实现，包括双边与单边旋转法及其并行算法。

鉴于矩阵的奇异值分解SVD在工程领域的广泛应用（如数据压缩、噪声去除、数值分析等等，包括在NLP领域的潜在语义索引LSI核心操作也是SVD），今天就详细介绍一种SVD的实现方法--Jacobi旋转法。跟其它SVD算法相比，Jacobi法精度高，虽然速度慢，但容易并行实现。

一些链接

http://cdmd.cnki.com.cn/Article/CDMD-10285-1012286387.htm 并行JACOBI方法求解矩阵奇异值的研究。本文呈现的代码就是依据这篇论文写出来的。

http://math.nist.gov/javanumerics/jama/ Jama包是用于基本线性代数运算的java包，提供矩阵的cholesky分解、LUD分解、QR分解、奇异值分解，以及PCA中要用到的特征值分解，此外可以计算矩阵的乘除法、矩阵的范数和条件数、解线性方程组等。

http://users.telenet.be/paul.larmuseau/SVD.htm 在线SVD运算器。

http://www.bluebit.gr/matrix-calculator/ bluebit在线矩阵运算器，提供矩阵的各种运算。

http://www.drque.net/Projects/Matrix/ C++ Matrix library提供矩阵的加减乘除、求行列式、LU分解、求逆、求转置。本文的头两段程序就引用了这里面的matrix.h。

基于双边Jacobi旋转的奇异值分解算法

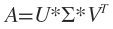
V是A的右奇异向量，也是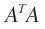的特征向量;

U是A的左奇异向量，也是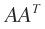的特征向量。

特别地，当A是对称矩阵的时候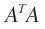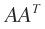，=，即U=V，U的列向量不仅是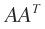的特征向量，也是A的特征向量。这一点在主成分分析中会用到。

对于正定的对称矩阵，奇异值等于特征值，奇异向量等于特征向量。特征值分解和奇异值分解的关系知乎上解释得很好。

U、V都是正交矩阵，满足矩阵的转置即为矩阵的逆。

双边Jacobi方法本来是用来求解对称矩阵的特征值和特征向量的，由于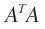就是对称矩阵，求出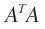的特征向量就求出了A的右奇异值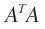，的特征值开方后就是A的奇异值。

一个Jacobi旋转矩阵J形如：

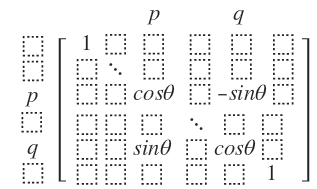
它就是在一个单位矩阵的基础上改变p行q行p列q列四个交点上的值，J矩阵是一个标准正交矩阵。

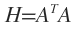当我们要对H和p列和q列进行正交变换时，就对H施行：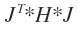

在一次迭代过程当中需要对A的任意两列进行一次正交变换，迭代多次等效于施行

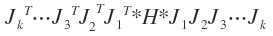
迭代的终止条件是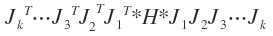为对角矩阵，即原矩阵H进过多次的双边Jacobi旋转后非对角线元素全部变成了0（实现计算当中不可能真的变为0，只要小于一个很小的数就可以认为是0了）。

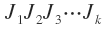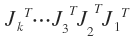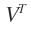每一个J都是标准正交阵，所以也是标准正交阵，记为V，则是，则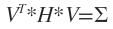。从此式也可以看出对称矩阵的左奇异向量和右奇异向量是相等的。V也是H的特征向量。

当特征值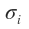是0时，对应的U_i和V_i不用求，我们只需要U和V的前r列就可以恢复矩阵A了（r是非0奇异值的个数），这也正是奇异值分解可以进行数据压缩的原因。

#include"matrix.h"
#include<cmath>
#include<map>
 
using namespace std;
 
const double THRESHOLD = 1E-8;
const int ITERATION = 30;   //迭代次数的上限
 
inline int sign(double number)
{
    if (number < 0)
        return -1;
    else
        return 1;
}
 
void rotate(Matrix < double >&matrix, int i, int j, bool & pass,
        Matrix < double >&J)
{
    double ele = matrix.get(i, j);
    if (fabs(ele) < THRESHOLD) {
        return;
    }
    pass = false;
    double ele1 = matrix.get(i, i);
    double ele2 = matrix.get(j, j);
    int size=matrix.getRows();
    double tao = (ele1 - ele2) / (2 * ele);
    double tan = sign(tao) / (fabs(tao) + sqrt(1 + pow(tao, 2)));
    double cos = 1 / sqrt(1 + pow(tan, 2));
    double sin = cos * tan;
    Matrix < double >G(IdentityMatrix < double >(size, size));
    G.put(i, i, cos);
    G.put(i, j, -1 * sin);
    G.put(j, i, sin);
    G.put(j, j, cos);
    matrix = G.getTranspose() * matrix * G;
    J *= G;
}
 
void jacobi(Matrix < double >&matrix, int size, vector < double >&E,
        Matrix < double >&J)
{
 
    int iteration = ITERATION;
    while (iteration-- > 0) {
        bool pass = true;
        for (int i = 0; i < size; ++i) {
            for (int j = i+1; j < size; ++j) {
                rotate(matrix, i, j, pass, J);
            }
        }
        if (pass)   //当非对角元素全部变为0时迭代退出
            break;
    }
    cout << "迭代次数：" << ITERATION - iteration << endl;
    for (int i = 0; i < size; ++i) {
        E[i] = matrix.get(i, i);
        if (E[i] < THRESHOLD)
            E[i] = 0.0;
    }
}
 
void svd(Matrix < double >&A, Matrix < double >&U, Matrix < double >&V,
     vector < double >&E)
{
    int rows = A.getRows();
    int columns = A.getColumns();
    assert(rows <= columns);
    assert(U.getRows() == rows);
    assert(U.getColumns() == rows);
    assert(V.getRows() == columns);
    assert(V.getColumns() == columns);
    assert(E.size() == columns);
    Matrix < double >B = A.getTranspose() * A;    //A的转置乘以A，得到一个对称矩阵B
    Matrix < double >J(IdentityMatrix < double >(columns, columns));
    vector < double >S(columns);
    jacobi(B, columns, S, J);   //求B的特征值和特征向量
    for (int i = 0; i < S.size(); ++i)
        S[i] = sqrt(S[i]);  //B的特征值开方后得到A的奇异值
 
    /*奇异值按递减排序，对应的V中的特征向量也要重排序 */
    multimap < double, int >eigen;
    for (int i = 0; i < S.size(); ++i)   //在multimap内部自动按key进行排序
        eigen.insert(make_pair(S[i], i));
    multimap < double, int >::const_iterator iter = --eigen.end();
    int num_eig = 0;    //记录非0奇异值的个数
    for (int i = 0; i < columns; ++i, iter--) {  //反向遍历multimap,使奇异值从大到小排序
        int index = iter->second;
        E[i] = S[index];
        if (E[i] > THRESHOLD) {
            num_eig++;
        }
        for (int row = 0; row < columns; ++row)
            V.put(row, i, J.get(row, index));
    }
 
    assert(num_eig <= rows);
    for (int i = 0; i < num_eig; ++i) {
        Matrix < double >vi = V.getColumn(i); //获取V的第i列
        double sigma = E[i];
        Matrix < double >ui(rows, 1);
        ui = A * vi;
        for (int j = 0; j < rows; ++j) {
            U.put(j, i, ui.get(j, 0) / sigma);
        }
    }
     
    //U矩阵的后(rows-none_zero)列就不计算了，采用默认值0。因为这后几列对应的奇异值为0,在做数据压缩时用不到这几列   
}
 
int main(int argc, char *argv[])
{
    const int ROW = 2;
    const int COL = 3;
    assert(ROW <= COL);
    double arr[ROW * COL] = {1,1,0,0,0,1};
    Matrix < double >A(ROW, COL);
    A = arr;
 
    Matrix < double >U(ROW, ROW);
    Matrix < double >V(COL, COL);
    vector < double >E(COL);
    svd(A, U, V, E);
    Matrix < double >Sigma(ROW, COL);
    for (int i = 0; i < ROW; ++i)
        Sigma.put(i, i, E[i]);
 
    cout << "U=" << endl << U;
    cout << "SIGMA=" << endl << Sigma;
    cout << "V^T=" << endl << V.getTranspose();
 
    Matrix < double >A_A = U * Sigma * V.getTranspose();
    cout << "reset A=" << endl << A_A;
 
    return 0;
}

基于单边Jacobi旋转的SVD算法

相对于双边，单边的计算量小，并且容易并行实现。

单边Jacobi方法直接对原矩阵A进行单边正交旋转，A可以是任意矩阵。

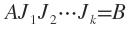
同样每一轮的迭代都要使A的任意两列都正交一次，迭代退出的条件是B的任意两列都正交。

单边Jacobi旋转有这么一个性质：旋转前若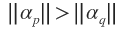，则旋转后依然是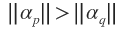；反之亦然。

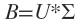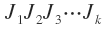把矩阵B每列的模长提取出来，，把记为V，则。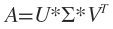

#include"matrix.h"
#include<cmath>
 
using namespace std;
 
const double THRESHOLD = 1E-8;
const int ITERATION = 30;   //迭代次数的上限
 
inline int sign(double number)
{
    if (number < 0)
        return -1;
    else
        return 1;
}
 
void orthogonal (Matrix < double >&matrix, int i, int j, bool & pass,Matrix < double >&V)
{
    assert(i<j);
    Matrix<double> Ci=matrix.getColumn(i);
    Matrix<double> Cj=matrix.getColumn(j);
    double ele = ((Ci.getTranspose())*Cj).get(0,0);
    if(fabs(ele)<THRESHOLD)          //i,j两列已经正交
        return;
    int rows=matrix.getRows();
    int columns=matrix.getColumns();    
     
    pass = false;
    double ele1 = ((Ci.getTranspose())*Ci).get(0,0);
    double ele2 = ((Cj.getTranspose())*Cj).get(0,0);
     
    /*只要每次旋转前都把范数大的列放在前面，就可以保证求出的奇异值是递减排序的*/
    if(ele1<ele2){           //如果matrix第i列的范数小于第j列，则交换两列.同时V矩阵也作相应的调换
        for(int row=0;row<rows;++row){
            matrix.put(row,i,Cj.get(row,0));
            matrix.put(row,j,Ci.get(row,0));
        }
        for(int row=0;row<columns;++row){
            double tmp=V.get(row,i);
            V.put(row,i,V.get(row,j));
            V.put(row,j,tmp);
        }
    }
         
    double tao = (ele1 - ele2) / (2 * ele);
    double tan = sign(tao) / (fabs(tao) + sqrt(1 + pow(tao, 2)));
    double cos = 1 / sqrt(1 + pow(tan, 2));
    double sin = cos * tan;
    for(int row=0;row<rows;++row){
        double var1=matrix.get(row,i)*cos+matrix.get(row,j)*sin;
        double var2=matrix.get(row,j)*cos-matrix.get(row,i)*sin;
        matrix.put(row,i,var1);
        matrix.put(row,j,var2);
    }
    for(int col=0;col<columns;++col){
        double var1=V.get(col,i)*cos+V.get(col,j)*sin;
        double var2=V.get(col,j)*cos-V.get(col,i)*sin;
        V.put(col,i,var1);
        V.put(col,j,var2);
    }
}
 
void hestens_jacobi(Matrix < double >&matrix, Matrix < double >&V)
{
    int rows=matrix.getRows();
    int columns=matrix.getColumns();
     
    int iteration = ITERATION;
    while (iteration-- > 0) {
        bool pass = true;
        for (int i = 0; i < columns; ++i) {
            for (int j = i+1; j < columns; ++j) {
                orthogonal(matrix, i, j, pass, V);      //经过多次的迭代正交后，V就求出来了
            }
        }
        if (pass)   //当任意两列都正交时退出迭代
            break;
    }
    cout << "迭代次数：" << ITERATION - iteration << endl;
}
 
int svn(Matrix < double >&matrix, Matrix < double >&S, Matrix < double >&U, Matrix < double >&V)
{
    int rows=matrix.getRows();
    int columns=matrix.getColumns();
    assert(rows<=columns);
     
    hestens_jacobi(matrix,V);
     
    vector<double> E(columns);        //E中存放奇异值
    int none_zero=0;        //记录非0奇异值的个数
    for (int i = 0; i < columns; ++i) {
        double norm=sqrt((matrix.getColumn(i).getTranspose()*(matrix.getColumn(i))).get(0,0));
        if(norm>THRESHOLD){
            none_zero++;
        }
        E[i]=norm;              
    }
     
    /**
    * U矩阵的后(rows-none_zero)列以及V的后(columns-none_zero)列就不计算了，采用默认值0。
    * 对于奇异值分解A=U*Sigma*V^T，我们只需要U的前r列，V^T的前r行（即V的前r列），就可以恢复A了。r是A的秩
    */
    for(int row=0;row<rows;++row){
        S.put(row,row,E[row]);
        for(int col=0;col<none_zero;++col){
            U.put(row,col,matrix.get(row,col)/E[col]);
        }
    }
     
    return none_zero;   //非奇异值的个数亦即矩阵的秩
}
 
int main(int argc, char *argv[])
{
    const int ROW = 3;
    const int COL = 6;
    assert(ROW <= COL);
    double arr[ROW * COL] = {6,5,1,9,8,4,8,5,2,4,6,9,1,2,3,2,1,4};
    Matrix < double >A(ROW, COL);
    A = arr;
 
    Matrix < double >U(ROW, ROW);
    IdentityMatrix < double >V(COL, COL);     //V初始时是一个单位矩阵
    Matrix < double >S(ROW, COL);
    int rank=svn(A,S,U,V);
 
    cout << "U=" << endl << U;
    cout << "SIGMA=" << endl << S;
    cout << "V^T=" << endl << (V.getTranspose());
 
    Matrix < double >A_A = U * S * (V.getTranspose());
    cout << "reset A=" << endl << A_A;
 
    return 0;
}

基于单边Jacobi旋转的SVD并行算法

单边Jacobi之于双边Jacobi的一个不同就是每次旋转只影响到矩阵A的两列，因经很多列对的正交旋转变换是可以并行执行的。

基本思想是将A按列分块，每一块分配到一个计算节点上，块内任意两列之间进行单边Jacobi正交变换，所有的计算节点可以同时进行。问题就是矩阵块内部列与列之间进行正交变换是不够的，我们需要所有矩阵块上的任意两列之间都进行正交变换，这就需要计算节点之间交换矩阵的列。本文采用奇偶序列的方法，具体可参考文章 http://cdmd.cnki.com.cn/Article/CDMD-10285-1012286387.htm。

由于这次我用的是C版的MPI（MPI也有C++和Fortan版的），所以上面代码用到的C++版的matrix.h就不能用了，需要自己写一个C版的matrix.h。

matrix.h

#ifndef _MATRIX_H
#define _MATRIX_H
   
#include<assert.h>
#include<stdlib.h>
#include<stdio.h>
 
//初始化一个二维矩阵
double** getMatrix(int rows,int columns){
    double **rect=(double**)calloc(rows,sizeof(double*));
    int i;
    for(i=0;i<rows;++i)
        rect[i]=(double*)calloc(columns,sizeof(double));
    return rect;
}
 
//返回一个单位矩阵
double** getIndentityMatrix(int rows){
    double** IM=getMatrix(rows,rows);
    int i;
    for(i=0;i<rows;++i)
        IM[i][i]=1.0;
    return IM;
}
   
//返回一个矩阵的副本
double** copyMatrix(double** matrix,int rows,int columns){
    double** rect=getMatrix(rows,columns);
    int i,j;
    for(i=0;i<rows;++i)
        for(j=0;j<columns;++j)
            rect[i][j]=matrix[i][j];
    return rect;
}
 
//从一个一维矩阵得到一个二维矩阵
void getFromArray(double** matrix,int rows,int columns,double *arr){
    int i,j,k=0;
    for(i=0;i<rows;++i){
        for(j=0;j<columns;++j){
            matrix[i][j]=arr[k++];
        }
    }
}
 
//打印二维矩阵
void printMatrix(double** matrix,int rows,int columns){
    int i,j;
    for(i=0;i<rows;++i){
        for(j=0;j<columns;++j){
            printf("%-10f\t",matrix[i][j]);
        }
        printf("\n");
    }
}
 
//释放二维矩阵
void freeMatrix(double** matrix,int rows){
    int i;
    for(i=0;i<rows;++i)
        free(matrix[i]);
    free(matrix);
}
   
//获取二维矩阵的某一行
double* getRow(double **matrix,int rows,int columns,int index){
    assert(index<rows);
    double *rect=(double*)calloc(columns,sizeof(double));
    int i;
    for(i=0;i<columns;++i)
        rect[i]=matrix[index][i];
    return rect;
}
 
//获取二维矩阵的某一列  
double* getColumn(double **matrix,int rows,int columns,int index){
    assert(index<columns);
    double *rect=(double*)calloc(rows,sizeof(double));
    int i;
    for(i=0;i<rows;++i)
        rect[i]=matrix[i][index];
    return rect;
}
 
//设置二维矩阵的某一列   
void setColumn(double **matrix,int rows,int columns,int index,double *arr){
    assert(index<columns);
    int i;
    for(i=0;i<rows;++i)
        matrix[i][index]=arr[i];
}
 
//交换矩阵的某两列
void exchangeColumn(double **matrix,int rows,int columns,int i,int j){
    assert(i<columns);
    assert(j<columns);
    int row;
    for(row=0;row<rows;++row){
        double tmp=matrix[row][i];
        matrix[row][i]=matrix[row][j];
        matrix[row][j]=tmp;
    }
}
 
 
//得到矩阵的转置
double** getTranspose(double **matrix,int rows,int columns){
    double **rect=getMatrix(columns,rows);
    int i,j;
    for(i=0;i<columns;++i){
        for(j=0;j<rows;++j){
            rect[i][j]=matrix[j][i];
        }
    }
    return rect;
}
 
//计算两向量内积
double vectorProduct(double *vector1,double *vector2,int len){
    double rect=0.0;
    int i;
    for(i=0;i<len;++i)
        rect+=vector1[i]*vector2[i];
    return rect;
}
 
//两个矩阵相乘
double** matrixProduct(double **matrix1,int rows1,int columns1,double **matrix2,int columns2){
    double **rect=getMatrix(rows1,columns2);
    int i,j;
    for(i=0;i<rows1;++i){
        for(j=0;j<columns2;++j){
            double *vec1=getRow(matrix1,rows1,columns1,i);
            double *vec2=getColumn(matrix2,columns1,columns2,j);
            rect[i][j]=vectorProduct(vec1,vec2,columns1);
            free(vec1);
            free(vec2);
        }
    }
    return rect;
}
 
//得到某一列元素的平方和
double getColumnNorm(double** matrix,int rows,int columns,int index){
    assert(index<columns);
    double* vector=getColumn(matrix,rows,columns,index);
    double norm=vectorProduct(vector,vector,rows);
    free(vector);
    return norm;
}
 
//打印向量
void printVector(double* vector,int len){
    int i;
    for(i=0;i<len;++i)
        printf("%-15.8f\t",vector[i]);
    printf("\n");
}
   
#endif

svd.c

#include"mpi.h"
#include"matrix.h"
#include<string.h>
#include<stdlib.h>
#include<math.h>      //gcc编译的时候需要加-lm选项
  
#define THREASHOLD 1e-8
#define ITERATION 20
#define  ROW 3  //每个计算节点上的矩阵块有3行4列
#define COL 3
#define LINELEN 5*COL       //矩阵文件每一行的长度
  
int sign(double number) {
    if(number<0)
        return -1;
    else
        return 1; 
}
  
int myRank;     //计算结点的序号
int procSize;   //计算结点的数目
MPI_Status status;      //存储状态变量
  
/*从文件中读取矩阵*/
void readFromFile(double **matrix,int row,int col,char* file){
    FILE *fp;
    int len=col*10;
    char *buf=(char*)calloc(len,sizeof(char));
    if((fp=fopen(file,"r"))==NULL){
        perror("fopen");
        printf("%s\n",file);
        exit(1);
    }
    int i,j;
    for(i=0;i<row;++i){
        if(fgets(buf,len,fp)==NULL){
            fprintf(stderr,"文件的行数小于矩阵需要的行数\n");
            exit(1);
        }
        char *seg=strtok(buf,"\t");
        double ele=atof(seg);
        matrix[i][0]=ele;
        for(j=1;j<col;++j){
            if((seg=strtok(NULL,"\t"))==NULL){
                fprintf(stderr,"文件的列数小于矩阵需要的列数\n");
                exit(1);
            }
            ele=atof(seg);
            matrix[i][j]=ele;
        }
        memset(buf,0x00,len);
    }
    free(buf);
    fclose(fp);
}
  
/*把矩阵写入文件*/
void writeToFile(double **matrix,int rows,int columns,char* file){
    FILE *fp;
    if((fp=fopen(file,"w"))==NULL){
        perror("fopen");
        exit(1);
    }
    fprintf(fp,"%d\t%d\n",rows,columns);        //文件首行记录矩阵的行数和列数
    int i,j;
    for(i=0;i<rows;++i){
        for(j=0;j<columns;++j){
            fprintf(fp,"%-10f\t",matrix[i][j]);
        }
        fprintf(fp,"\n");
    }
    fclose(fp);
}
  
/*把向量写入文件*/
void vectorToFile(double *vector,int len,char* file){
    FILE *fp;
    if((fp=fopen(file,"w"))==NULL){
        perror("fopen");
        exit(1);
    }
    int i;
    for(i=0;i<len;++i){
        fprintf(fp,"%-10f\t",vector[i]);
    }
    fclose(fp);
}
  
/*两个向量进行单边Jacobi正交变换*/
void orthogonalVector(double *Ci,double *Cj,int len1,double *Vi,double *Vj,int len2,int *pass){
    double ele=vectorProduct(Ci,Cj,len1);
    if(fabs(ele)<THREASHOLD)
        return;     //如果两列已经正交，不需要进行变换，则返回true
    *pass=0;
    double ele1=vectorProduct(Ci,Ci,len1);
    double ele2=vectorProduct(Cj,Cj,len1);
      
      
  
    double tao=(ele1-ele2)/(2*ele);
    double tan=sign(tao)/(fabs(tao)+sqrt(1+pow(tao,2)));
    double cos=1/sqrt(1+pow(tan,2));
    double sin=cos*tan;
      
    int row;
    for(row=0;row<len1;++row){
        double var1=Ci[row]*cos+Cj[row]*sin;
        double var2=Cj[row]*cos-Ci[row]*sin;
  
            Ci[row]=var1;
            Cj[row]=var2;
  
    }
    for(row=0;row<len2;++row){
        double var1=Vi[row]*cos+Vj[row]*sin;
        double var2=Vj[row]*cos-Vi[row]*sin;
  
            Vi[row]=var1;
            Vj[row]=var2;
  
    }
}

/*矩阵的两列进行单边Jacobi正交变换。V是方阵，行/列数为columns*/
void orthogonal(double **matrix,int rows,int columns,int i,int j,int *pass,double **V){
    assert(i<j);
       
    double* Ci=getColumn(matrix,rows,columns,i);
    double* Cj=getColumn(matrix,rows,columns,j);
    double* Vi=getColumn(V,columns,columns,i);
    double* Vj=getColumn(V,columns,columns,j);
    orthogonalVector(Ci,Cj,rows,Vi,Vj,columns,pass);
       
    int row;
    for(row=0;row<rows;++row){
        matrix[row][i]=Ci[row];
        matrix[row][j]=Cj[row];
    }
    for(row=0;row<columns;++row){
        V[row][i]=Vi[row];
        V[row][j]=Vj[row];
    }
    free(Ci);
    free(Cj);
    free(Vi);
    free(Vj);
}
  
void normalize(double **A,int rows,int columns){
    double *sigular=(double*)calloc(columns,sizeof(double));
    int i,j;
    for(i=0;i<columns;++i){
        double *vector=getColumn(A,rows,columns,i);
        double norm=sqrt(vectorProduct(vector,vector,rows));
        sigular[i]=norm;
    }
    char outFileS[7]={'S','X','.','m','a','t','\0'};
    outFileS[1]='0'+myRank;
    vectorToFile(sigular,columns,outFileS);
    double **U=getMatrix(rows,columns);
    for(j=0;j<columns;++j){
        if(sigular[j]==0)
            for(i=0;i<rows;++i)
                U[i][j]=0;
        else
            for(i=0;i<rows;++i)
                U[i][j]=A[i][j]/sigular[j];
    }
    char outFileU[7]={'U','X','.','m','a','t','\0'};
    outFileU[1]='0'+myRank;
    writeToFile(U,rows,columns,outFileU);
    free(sigular);
    freeMatrix(U,rows);
}
  
void main(int argc, char *argv[])
{
    MPI_Init(&argc,&argv);
    MPI_Comm_rank(MPI_COMM_WORLD,&myRank);
    MPI_Comm_size(MPI_COMM_WORLD,&procSize);
      
    assert(myRank<10);
    int totalColumn=COL*procSize;       //算出原矩阵总共有多少列
      
    /*准备矩阵块A和V*/
    char matrixFile[11]={'b','l','o','c','k','X','.','m','a','t','\0'};
    matrixFile[5]='0'+myRank;
    double **A=getMatrix(ROW,COL);
    readFromFile(A,ROW,COL,matrixFile);
    double **V=getMatrix(totalColumn,COL);
    int j;
    for(j=0;j<COL;++j){
        V[COL*myRank+j][j]=1.0;
    }
      
    /*开始进行单边Jacobi旋转迭代*/
    int iteration=ITERATION;
    while(iteration-->0){
        /*奇数次迭代后矩阵按列范数从大到小排列；偶数次迭代后矩阵按列范数从小到大排列*/
        int pass=1;
        int allpass=0;
        /*每个计算节点上相邻两列进行单边Jacobi变换*/
        int i;
        for(i=1;i<=totalColumn;++i){     //原矩阵有几列就需要做几轮的交换
            int j;
            int send=0,recv=0;  //send记录是否要把本矩阵块的最后一列发送给下一个计算结点；recv记录是否要从上一个计算结点接收一列数据
            int mod1=i%2;       //余数为0时是奇序，否则为偶序
            int mod2=(myRank*COL)%2;    //判断本块的第1列(首列)是否为原矩阵的第奇数列，为0则是，为1则不是
            if(mod1^mod2){      //融合了奇序和偶序的情况
                j=0;        //首列可以和第二列进行正交变换
            }
            else{
                j=1;        //首列需要和上一个计算结点的最后一列进行正交变换
                if(myRank>0){        //不是第1个计算节点
                    recv=1;     //需要从上一个计算节点接收最后一列
                }
            }
            for(++j;j<COL;j+=2){     //第j列与j-1列进行单边Jacobi正交变换
                orthogonal(A,ROW,COL,j-1,j,&pass,V,totalColumn);
                exchangeColumn(A,ROW,COL,j-1,j);        //正交变换之后交换两列
                exchangeColumn(V,totalColumn,COL,j-1,j);
            }
            if(j==COL){     //最后一列剩下了，无法配对，它需要发送给下一个计算节点
                if(myRank<procSize-1){   //如果不是最后1个计算节点
                    send=1;         //需要把最后一列发给下一个计算节点
                }
            }
            if(send){
                //把最后一列发给下一个计算节点
                double *lastColumnA=getColumn(A,ROW,COL,COL-1);
                double *lastColumnV=getColumn(V,totalColumn,COL,COL-1);
                MPI_Send(lastColumnA,ROW,MPI_DOUBLE,myRank+1,59,MPI_COMM_WORLD);
                MPI_Send(lastColumnV,totalColumn,MPI_DOUBLE,myRank+1,60,MPI_COMM_WORLD);
                free(lastColumnA);
                free(lastColumnV);
            }
            if(recv){
                //从上一个计算节点接收最后一列
                double* preColumnA=(double*)calloc(ROW,sizeof(double));
                double* preColumnV=(double*)calloc(totalColumn,sizeof(double));
                MPI_Recv(preColumnA,ROW,MPI_DOUBLE,myRank-1,59,MPI_COMM_WORLD,&status);
                MPI_Recv(preColumnV,totalColumn,MPI_DOUBLE,myRank-1,60,MPI_COMM_WORLD,&status);
                //本行首列与上一个计算节点末列进行正交变换
                double* firstColumnA=getColumn(A,ROW,COL,0);
                double* firstColumnV=getColumn(V,totalColumn,COL,0);
                orthogonalVector(preColumnA,firstColumnA,ROW,preColumnV,firstColumnV,totalColumn,&pass);
                //把preColumn留下
                setColumn(A,ROW,COL,0,preColumnA);
                setColumn(V,totalColumn,COL,0,preColumnV);
                //把firstColumn发送给上一个计算结点
                MPI_Send(firstColumnA,ROW,MPI_DOUBLE,myRank-1,49,MPI_COMM_WORLD);
                MPI_Send(firstColumnV,totalColumn,MPI_DOUBLE,myRank-1,50,MPI_COMM_WORLD);
                free(preColumnA);
                free(preColumnV);
                free(firstColumnA);
                free(firstColumnV);
            }
            if(send){
                //把最后一列发给下一个计算节点后，下一个计算节点做完了正交变换，又把一列发送回来了，现在需要接收
                double* nextColumnA=(double*)calloc(ROW,sizeof(double));
                double* nextColumnV=(double*)calloc(totalColumn,sizeof(double));
                MPI_Recv(nextColumnA,ROW,MPI_DOUBLE,myRank+1,49,MPI_COMM_WORLD,&status);
                MPI_Recv(nextColumnV,totalColumn,MPI_DOUBLE,myRank+1,50,MPI_COMM_WORLD,&status);
                //把接收到的那一列赋给本块的最后一列
                setColumn(A,ROW,COL,COL-1,nextColumnA);
                setColumn(V,totalColumn,COL,COL-1,nextColumnV);
                free(nextColumnA);
                free(nextColumnV);
            }
        }
        MPI_Barrier(MPI_COMM_WORLD);        //各个计算节点都完成一次迭代后，汇总一上是不是所有的都pass了
        MPI_Reduce(&pass,&allpass,1,MPI_INT,MPI_SUM,0,MPI_COMM_WORLD);
        MPI_Bcast(&allpass,1,MPI_INT,0,MPI_COMM_WORLD);         //把是否allpass告知所有节点
        if(allpass==procSize)
            break;      //退出迭代
    }
    if(myRank==0){
        printf("迭代次数:%d\n",ITERATION-iteration-1);
    }
    char outFileV[7]={'V','X','.','m','a','t','\0'};
    outFileV[1]='0'+myRank;
    writeToFile(V,totalColumn,COL,outFileV);
    normalize(A,ROW,COL);
    freeMatrix(A,ROW);
    freeMatrix(V,totalColumn);
    MPI_Finalize();
}