在边长为\(1\)的正方体\(ABCD-EFGH\)中,点\(M\)为线段\(BG\)上任意的动点,则\(|CM|+|MH|\)的最小值为\(\underline{\qquad\qquad}.\)
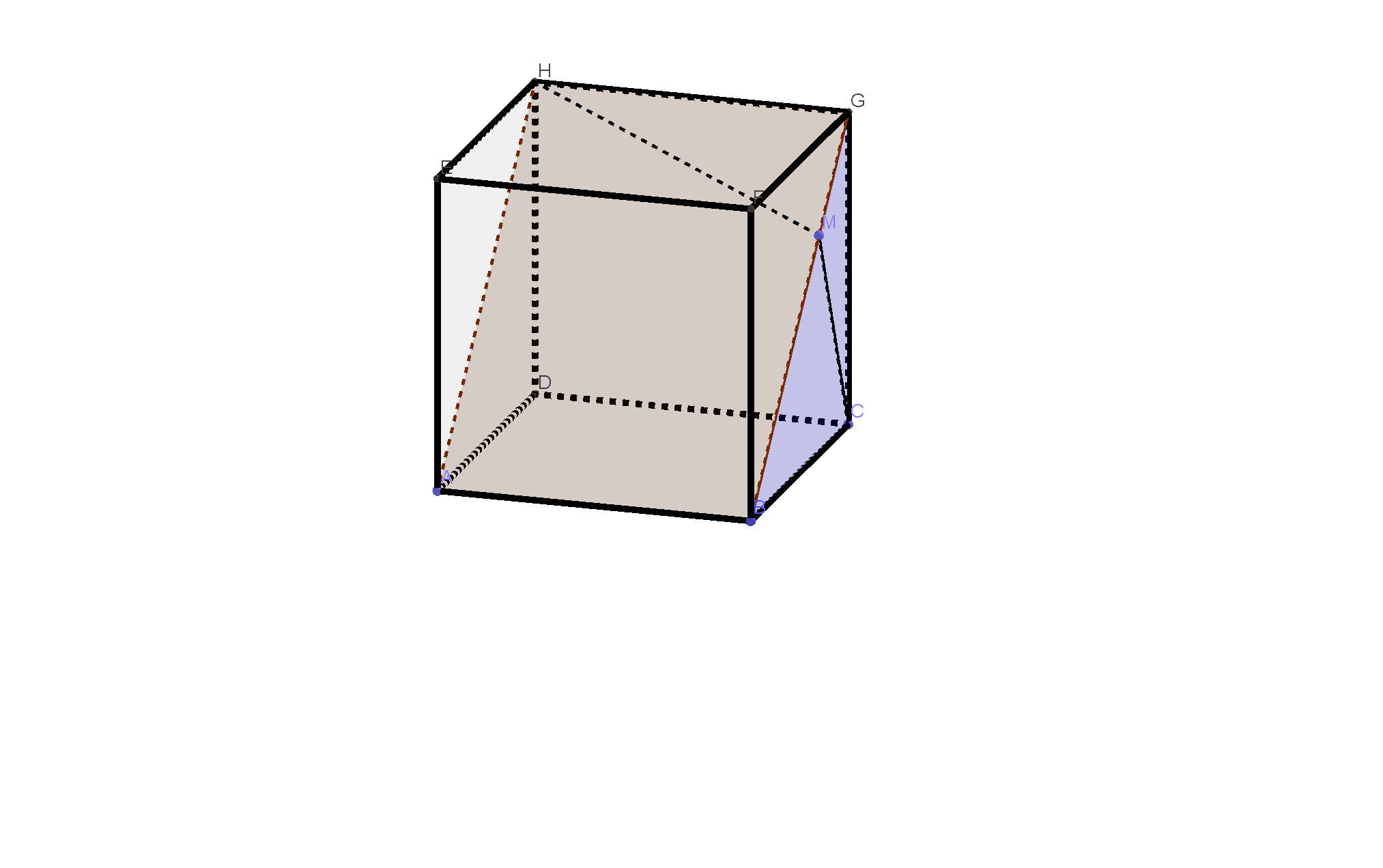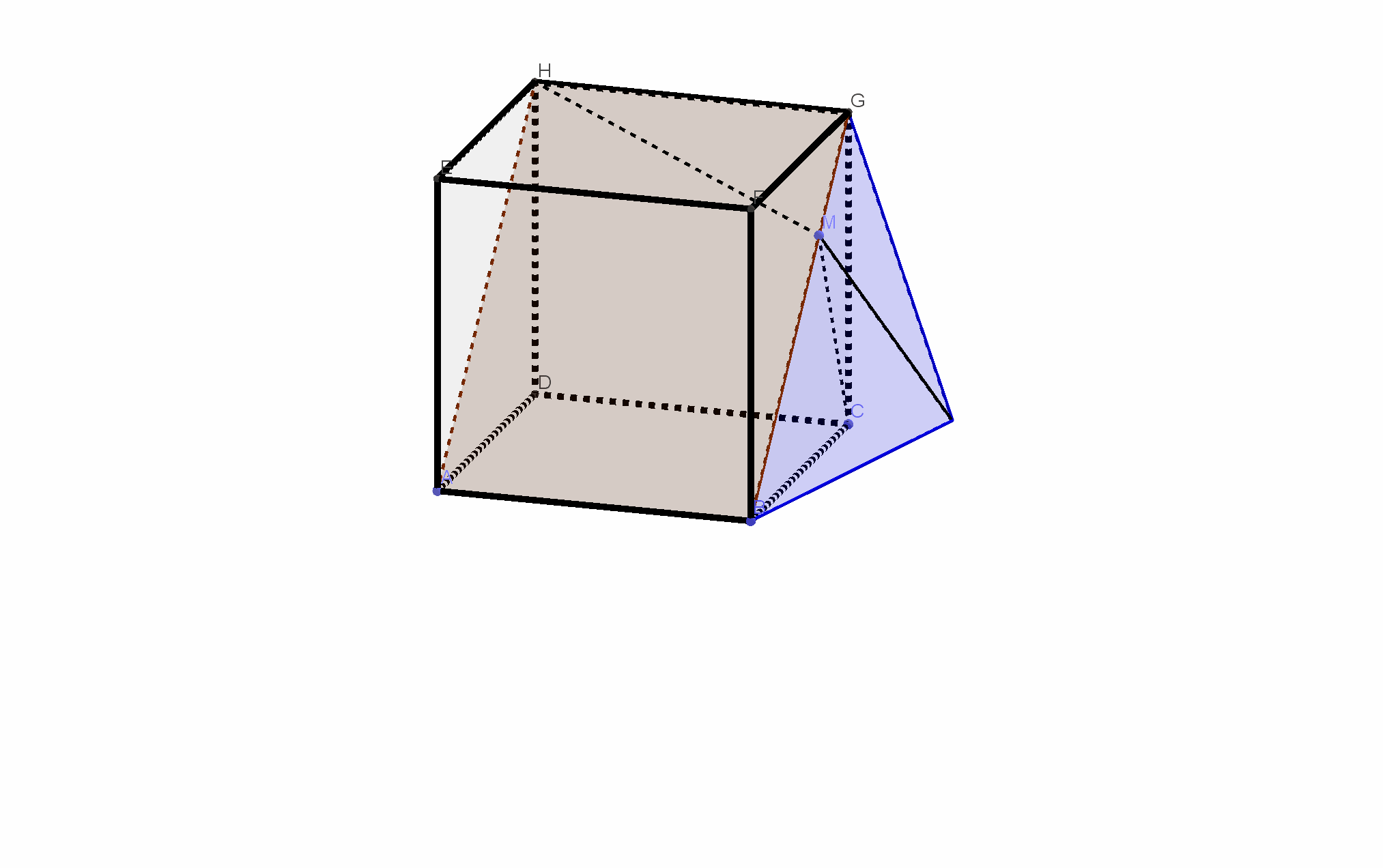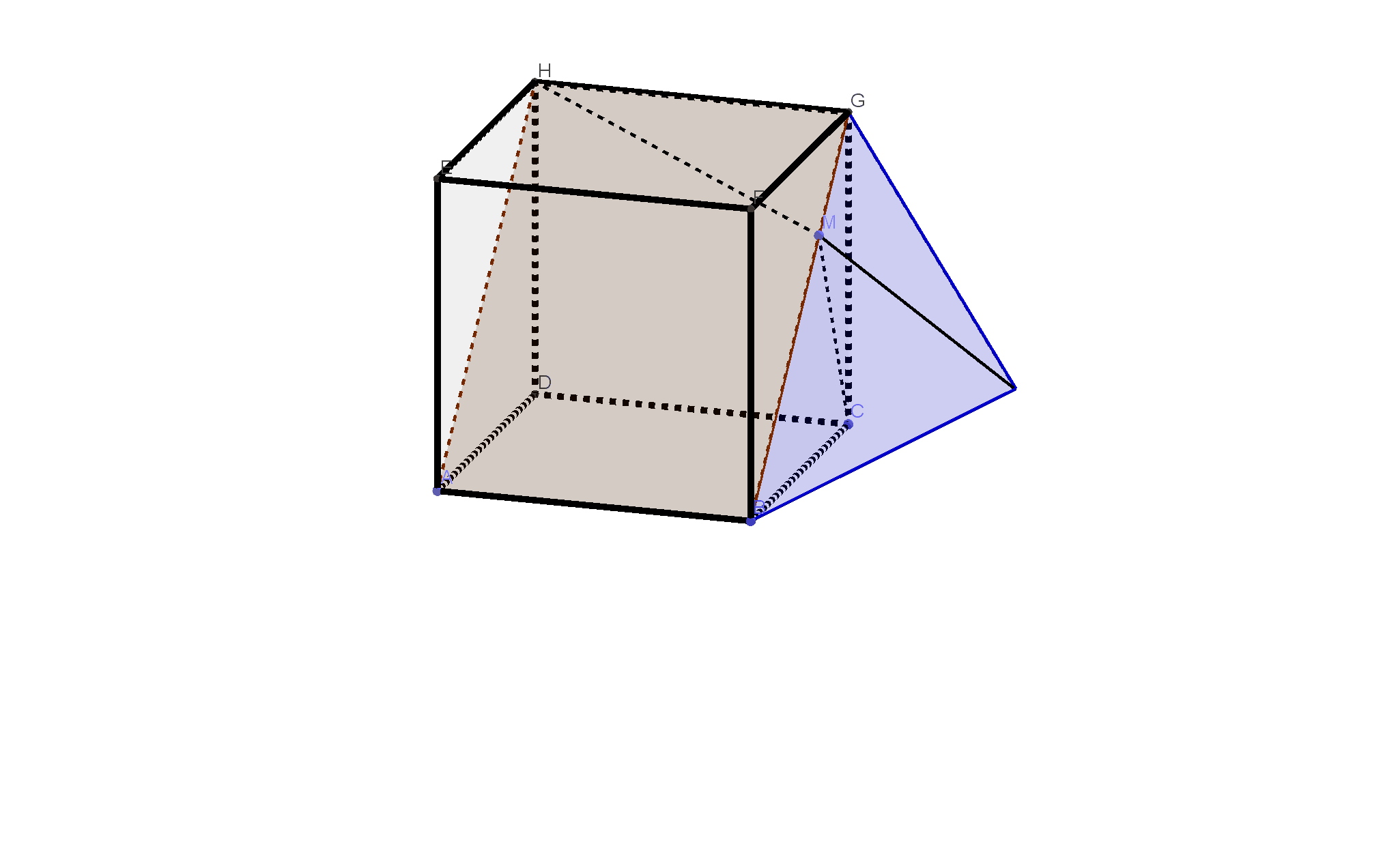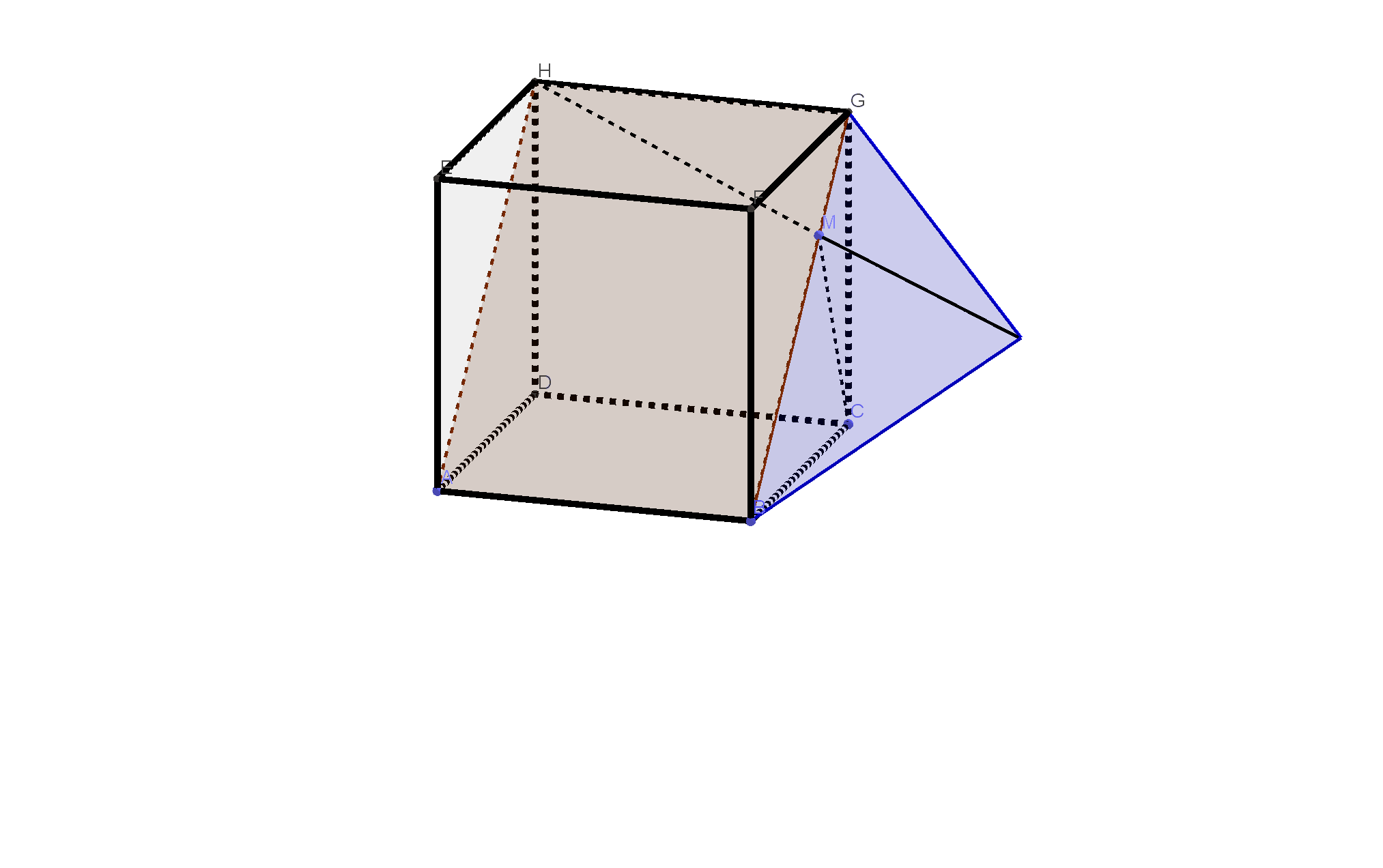
 博客给出一个边长为1的正方体ABCD - EFGH,提出点M为线段BG上任意动点时,求|CM| + |MH|的最小值问题,并给出了转载来源。
博客给出一个边长为1的正方体ABCD - EFGH,提出点M为线段BG上任意动点时,求|CM| + |MH|的最小值问题,并给出了转载来源。
在边长为\(1\)的正方体\(ABCD-EFGH\)中,点\(M\)为线段\(BG\)上任意的动点,则\(|CM|+|MH|\)的最小值为\(\underline{\qquad\qquad}.\)

转载于:https://www.cnblogs.com/xuebajunlutiji/p/10548484.html

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


