最长公共子序列

2019独角兽企业重金招聘Python工程师标准>>>

from: http://acm.nyist.net/JudgeOnline/problem.php?pid=36

描述： 最长公共子序列也称作最长公共子串(不要求连续)，英文缩写为LCS（Longest Common Subsequence）。其定义是，一个序列 S ，如果分别是两个或多个已知序列的子序列，且是所有符合此条件序列中最长的，则 S 称为已知序列的最长公共子序列。

输入

    第一行给出一个整数N(0<N<100)表示待测数据组数
    接下来每组数据两行，分别为待测的两组字符串。每个字符串长度不大于1000.

输出

    每组测试数据输出一个整数，表示最长公共子序列长度。每组结果占一行。

样例输入

2
asdf
adfsd
123abc
abc123abc

样例输出

3
6

Solution: 

直接上状态方程

    

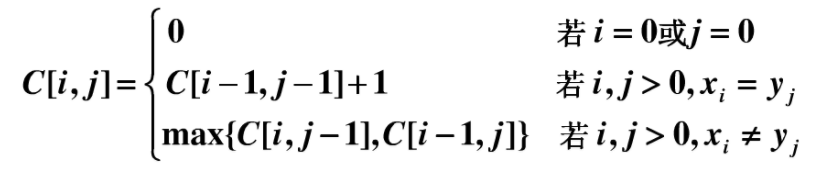
贴代码：

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;

/**
 * @create 2017-09-04 8:51
 */
public class Main {
    public static int longestCommonSubstring(String s1, String s2) {
        if (s1 == null || s2 == null) {
            return 0;
        }

        int[][] m = new int[s1.length() + 1][s2.length() + 1];
        //初始化边界条件
        for (int i = 0; i <= s1.length(); i++) { //每行第一列置0
            m[i][0] = 0;
        }
        for (int j = 0; j <= s2.length(); j++) { //每列第一行置0
            m[0][j] = 0;
        }

        int result = 0;
        for (int i = 1; i <= s1.length(); i++) {
            for (int j = 1; j <= s2.length(); j++) {
                if (s1.charAt(i - 1) == s2.charAt(j - 1)) {
                    m[i][j] = m[i - 1][j - 1] + 1;
                } else {
                    m[i][j] = Math.max(m[i - 1][j], m[i][j - 1]);
                }
                result = Math.max(m[i][j], result);
            }
        }

        return result;
    }

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int n = Integer.parseInt(br.readLine());
        while (n-- > 0) {
            System.out.println(longestCommonSubstring(br.readLine(), br.readLine()));
        }
        br.close();
    }
}

    要想把最长的公共字串打印出来，还是贴代码，直接看结果

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;

/**
 * @create 2017-09-04 8:51
 */
public class Main {
    public static String s1, s2;

    public static int[][] longestCommonSubstring() {
        if (s1 == null || s2 == null) {
            return null;
        }

        int[][] m = new int[s1.length() + 1][s2.length() + 1];
        //初始化边界条件
        for (int i = 0; i <= s1.length(); i++) { //每行第一列置0
            m[i][0] = 0;
        }
        for (int j = 0; j <= s2.length(); j++) { //每列第一行置0
            m[0][j] = 0;
        }

        for (int i = 1; i <= s1.length(); i++) {
            for (int j = 1; j <= s2.length(); j++) {
                if (s1.charAt(i - 1) == s2.charAt(j - 1)) {
                    m[i][j] = m[i - 1][j - 1] + 1;
                } else {
                    m[i][j] = Math.max(m[i - 1][j], m[i][j - 1]);
                }
            }
        }

        return m;
    }

    public static void printLCS(int[][] m, int i, int j) {//打印最长公共子序列
        if (i == 0 || j == 0) {
            return;
        }
//        System.out.println("i=" + i + ", j=" + j);
        if (s1.charAt(i - 1) == s2.charAt(j - 1)) {
            printLCS(m, i - 1, j - 1);
            System.out.print(s1.charAt(i - 1));
        } else if (m[i-1][j] >= m[i][j]){
            printLCS(m, i - 1, j);
        } else {
            printLCS(m, i, j - 1);
        }
    }

    public static void print(int[][] m) {   //打印矩阵
        for (int i = 0; i < m.length; i++) {
            for (int j = 0; j < m[i].length; j++) {
                if (i == 0 && j == 0) {
                    System.out.print("* ");
                } else if (i == 0) {
                    System.out.print(s2.charAt(j - 1) + " ");
                } else if (j == 0) {
                    System.out.print(s1.charAt(i - 1) + " ");
                } else {
                    System.out.print(m[i][j] + " ");
                }
            }
            System.out.println();
        }
    }
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int n = Integer.parseInt(br.readLine());
        while (n-- > 0) {
            s1 = br.readLine();
            s2 = br.readLine();

            int[][] m = longestCommonSubstring();
            print(m);
            printLCS(m, s1.length(), s2.length());
            System.out.println();
        }
        br.close();
    }
}

对于输入

1
asdf
asfsd

可以得到

* a d f s d 
a 1 1 1 1 1 
s 1 1 1 2 2 
d 1 2 2 2 3 
f 1 2 3 3 3 
asd

打印过程如下图

ps: 要想查看打印过程，将printLCS的第一个System.out.println的注释取消，将第二个System.out.print的注释加上

转载于:https://my.oschina.net/yitiaoxianyu/blog/1528706