美日汇率与美日股市指数关系分析

最新推荐文章于 2025-09-10 17:59:49 发布

weixin_34267123

最新推荐文章于 2025-09-10 17:59:49 发布

阅读量404

点赞数

CC 4.0 BY-SA版权

文章标签： python 数据结构与算法

原文链接：https://my.oschina.net/u/3093769/blog/856766

本文通过抓取美日汇率、日经指数和美国道指指数的数据，探索了美日汇率与美日股市指数差价之间的关系。利用R语言进行数据分析，发现两者存在强负相关性，并建立线性回归模型进行预测。

2019独角兽企业重金招聘Python工程师标准>>>

一、获取数据

在yahoo抓取自2012年以来，美日汇率、日经指数和美国道指指数价差。

> library(quantmod)
> Indexdata<-list()
> Index<-c("^N225","DJIA")
> IndexName<-c("N225","US30","USD/JPY")
> for(i in 1:2){
+ n<-Index[i]
+ res<-get(getSymbols(n,src="yahoo",from="2012-01-01",to=Sys.Date()))
+ cp<-res[,4]
+ Indexdata[[i]]<-cp
+ next}
> forex<-get(getFX("USD/JPY",from="2012-01-01",to=Sys.Date(),auto.assign=TRUE))
> Indexdata[[3]]<-forex
> Returndata<-do.call(merge,Indexdata)
> names(Returndata)<-IndexName
> mydata<-na.omit(Returndata)
> mydata$diff<-mydata$US30-mydata$N225
> getdata<-mydata[,3:4]
> head(getdata)    #查看前6条记录
           USD.JPY     diff
2012-03-12 82.2687 3069.850
2012-03-13 82.5322 3278.600
2012-03-14 83.3701 3143.580
2012-03-15 83.6701 3129.479
2012-03-16 83.5102 3102.790
2012-03-19 83.3502 3097.140
> tail(getdata)    #查看后6条记录
           USD.JPY     diff
2017-03-03 114.315 1536.541
2017-03-06 113.846 1575.199
2017-03-07 113.963 1580.609
2017-03-08 114.100 1601.701
2017-03-09 114.622 1539.609
2017-03-10 115.178 1298.371
> dim(getdata)
[1] 1199    2

二、数据的初步探索

输入图片说明

> cordata<-cor(getdata[,1:2])
> cordata
           USD.JPY       diff
USD.JPY  1.0000000 -0.9195801
diff    -0.9195801  1.0000000

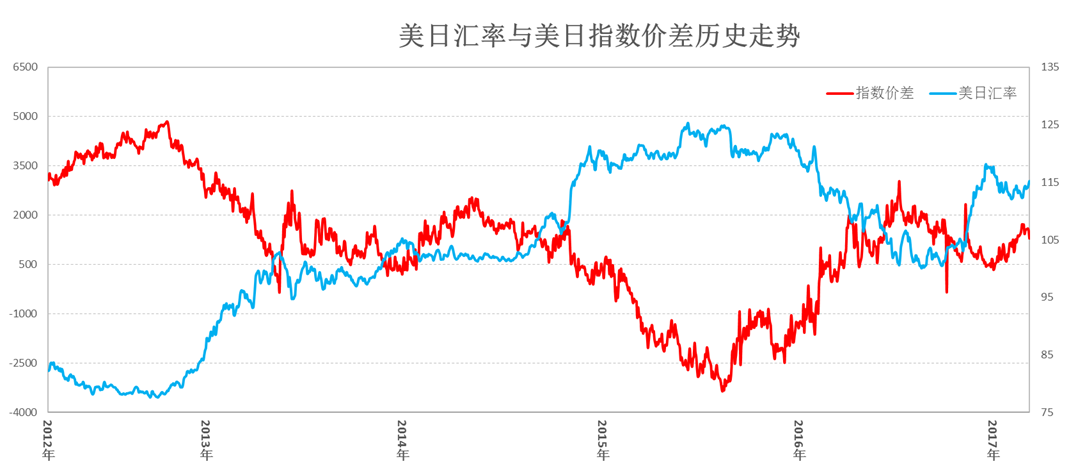
由上面可以看到，美日汇率与美日股市指数差价具有强负相关性。

三、构造线性回归模型

1、以汇率为因变量，指数价差为自变量：

> model<-lm(USD.JPY~diff,getdata)
> summary(model)

Call:
lm(formula = USD.JPY ~ diff, data = getdata)

Residuals:
     Min       1Q   Median       3Q      Max 
-10.8174  -4.4264  -0.7552   4.0511  13.7444 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept)  1.115e+02  1.799e-01  619.80   <2e-16 ***
                   diff        -6.825e-03  8.428e-05  -80.97   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 5.339 on 1197 degrees of freedom
Multiple R-squared:  0.8456,    Adjusted R-squared:  0.8455 
F-statistic:  6557 on 1 and 1197 DF,  p-value: < 2.2e-16

P值小，说明回归效果显著。

当美日股市指数差价为2000时，预测美日汇率：

> new<-data.frame(diff=2000)
> myforex<-predict(model,new,interval="prediction",level=0.95)
> myforex
       fit      lwr      upr
1 97.82946 87.34874 108.3102

转载于:https://my.oschina.net/u/3093769/blog/856766