岭回归是带二范数惩罚的最小二乘回归。
ols方法中,
<img src="https://i-blog.csdnimg.cn/blog_migrate/befa5893bea962a30d4925706236127f.png" data-rawwidth="253" data-rawheight="50" class="content_image" width="253">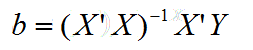
X‘X不能为0。当变量之间的相关性较强时,X‘X很小,甚至趋于0。
岭回归是一种专用于共线性数据分析的有偏估计回归方法,实质上是一种改良的最小二乘估计法,通过放弃最小二乘法的无偏性,以损失部分信息、降低精度为代价获得回归系数更为符合实际、更可靠的回归方法,对病态数据的拟合要强于OLS。本质是在自变量信息矩阵的主对角线元素上人为地加入一个非负因子。即:
<img src="https://i-blog.csdnimg.cn/blog_migrate/590768e812ad2136889e9ba0ead8f2bc.png" data-rawwidth="369" data-rawheight="54" class="content_image" width="369">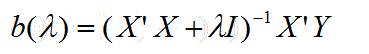
当λ=0时,b(λ)=b。b(λ)中各元素bi(λ)的绝对值均趋于不断变小(由于自变数间的相关,个别bi(λ)可能有小范围的向上波动或改变正、负号),它们对bi的偏差也将愈来愈大;如果λ->∞,则b(λ)->0。b(λ)随λ的改变而变化的轨迹,就称为岭迹。
应用场景就是处理高度相关的数据。画出岭迹图,选取稳定的那一段的lambda就好了。
ols方法中,
<img src="https://i-blog.csdnimg.cn/blog_migrate/befa5893bea962a30d4925706236127f.png" data-rawwidth="253" data-rawheight="50" class="content_image" width="253">
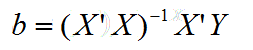
X‘X不能为0。当变量之间的相关性较强时,X‘X很小,甚至趋于0。
岭回归是一种专用于共线性数据分析的有偏估计回归方法,实质上是一种改良的最小二乘估计法,通过放弃最小二乘法的无偏性,以损失部分信息、降低精度为代价获得回归系数更为符合实际、更可靠的回归方法,对病态数据的拟合要强于OLS。本质是在自变量信息矩阵的主对角线元素上人为地加入一个非负因子。即:
<img src="https://i-blog.csdnimg.cn/blog_migrate/590768e812ad2136889e9ba0ead8f2bc.png" data-rawwidth="369" data-rawheight="54" class="content_image" width="369">
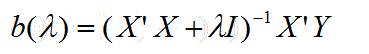
当λ=0时,b(λ)=b。b(λ)中各元素bi(λ)的绝对值均趋于不断变小(由于自变数间的相关,个别bi(λ)可能有小范围的向上波动或改变正、负号),它们对bi的偏差也将愈来愈大;如果λ->∞,则b(λ)->0。b(λ)随λ的改变而变化的轨迹,就称为岭迹。
应用场景就是处理高度相关的数据。画出岭迹图,选取稳定的那一段的lambda就好了。
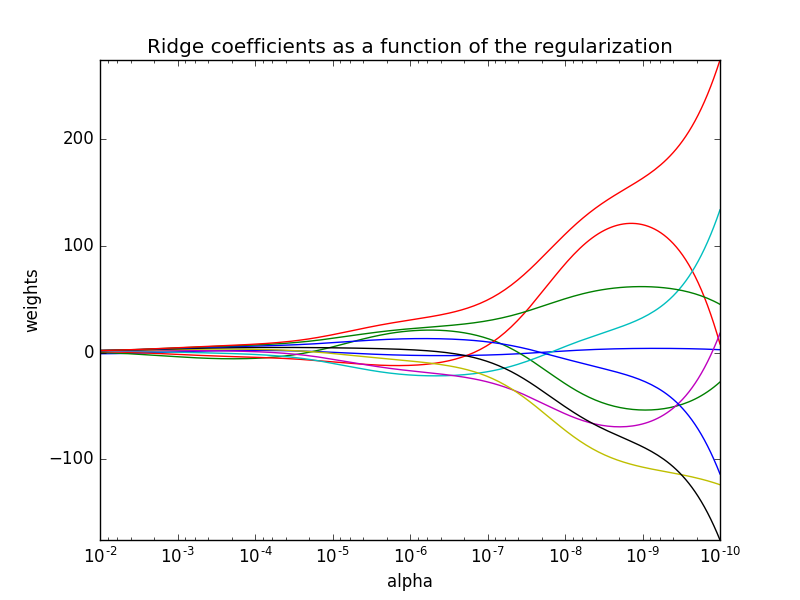
此图alpha对应公式中的lamda,b对应weights
病态矩阵:
判别分析的一个假设是用来判定组别的变量不能是完全冗余的变量。判别分析的计算过程中,要求模型中的变量方差/协方差矩阵的逆矩阵。如果变量是与另一个变量完全冗余的,这个矩阵称为病态矩阵,即矩阵不能求逆。例如,有一个变量是其他三个变量之和,这个变量也存在于模型中,这个矩阵就是病态矩阵。




 本文介绍了岭回归的基本原理,作为改进的最小二乘估计法,适用于处理高度相关的数据集。通过引入二范数惩罚项来克服多重共线性问题,并讨论了如何选择合适的惩罚参数λ。
本文介绍了岭回归的基本原理,作为改进的最小二乘估计法,适用于处理高度相关的数据集。通过引入二范数惩罚项来克服多重共线性问题,并讨论了如何选择合适的惩罚参数λ。
















 715
715

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








