leetcode 35 搜索插入位置

最新推荐文章于 2025-09-10 15:24:29 发布

转载最新推荐文章于 2025-09-10 15:24:29 发布 · 63 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/joelwang/p/10697696.html

文章标签：

#数据结构与算法

本文深入探讨了二分查找算法在有序数组中的应用，通过对比暴力解法和标准二分查找，详细解析了如何优化二分查找算法以提高搜索效率。文章提供了一种改进的二分查找实现方式，确保在目标值不存在于数组中时，能够准确找到插入位置。

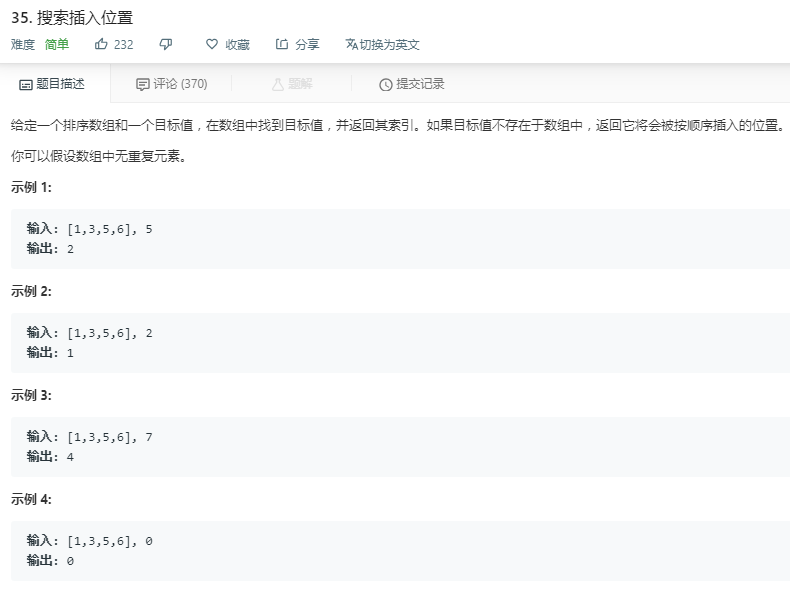
这种有序数组当然要用二分查找，但我在居然看到最优解居然是暴力解法，不知道到底是怎么判的；这个是不标准版本二分查找

class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        int left=0,right=nums.size()-1;
        while(left<right){
            int mid=(left+right)/2;
            if(nums[mid]==target)
                return mid;
            if(nums[mid]>target){
                right=mid-1;
            }else{
                left=mid+1;
            }
        }
        return nums[left]>=target?left:left+1;
    }
};

事实上，当right和left相邻时mid=（left+right）/2一定就是left,根据这个原理可以判断一定有mid<right;因此不妨保证nums[right]>target（即一开始令right=nums.size(),之后只有当nums[mid]>target时，更新right=target，这样可以从左边逼近目标）

因此最终的情况会是这样：

举个例子：对于的 1 3 5 7 9数组，寻找目标；

假如寻找3，那么最后有下标 left=0,right=2，nums[mid]==3找到目标；

假如找4，那么最后left=0,right=2,nums[mid]<4;更新left=mid+1；

即对于元素x如果序列中存在与它相等的元素，那么在最后一轮的mid中就可以找到；如果不存在，则可以保证最后left的值刚好是第一个比target大的元素；

之所以令right=nums.size()，除了利用从左边逼近可以保证数组不越界，还有就是为了处理当目标值比数组中所有元素都大的情况，此时left==right==nums.size()；

因此，代码可以这么写：

class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        int left=0,right=nums.size()-1;
        while(left<right){
            int mid=(left+right)/2;
            if(nums[mid]==target)
                return mid;
            if(nums[mid]>target){
                right=mid-1;
            }else{
                left=mid+1;
            }
        }
        return nums[left]>=target?left:left+1;
    }
};