本质图像论文笔记

• PAMI2015
  • Shape, Illumination, and Reflectance from Shading
• ICCV2015
  • Intrinsic Decomposition of Image Sequences from Local Temporal Variations
• PAMI2016
  • Intrinsic Scene Properties from a Single RGB-D Image
• ICCV2016
  • Deep Specialized Network for Illuminant Estimation
• ICCV2017
  • A Joint Intrinsic-Extrinsic Prior Model for Retinex
• CVPR2018
  • SfSNet: Learning Shape, Reflectance and Illuminance of Faces `in the Wild'
  • Attentive Generative Adversarial Network for Raindrop Removal from A Single Image
• ECCV2018
  • Single Image Intrinsic Decomposition without a Single Intrinsic Image
  • Joint Learning of Intrinsic Images and Semantic Segmentation
  • CGIntrinsics: Better Intrinsic Image Decomposition through Physically-Based Rendering
• BMVC2018
  • Deep Retinex Decomposition for Low-Light Enhancement

PAMI2015

Shape, Illumination, and Reflectance from Shading

作者：Jonathan T. Barron ， Jitendra Malik

对于一幅图像而言，要推断出图像的场景属性（shape, reflectance, illumination），也可以说是本质图像，是一件非常困难的事，因为有无数的形状、颜料和灯光可以精确地再现一幅图像。为了恢复出场景属性，需要对场景属性进行约束（也就是先验），作者基于在自然图像中出现的统计规律（这些规律是因为生成这些图像的底层世界的统计规律）对场景属性构建多种先验，对本质图像分解问题进行建模，进行统计推断， 得到最有可能的解释。

主要贡献：

• 将统计规则从自然图像中扩展到产生自然图像的世界；

• 第一个使用这些统计观测来同时恢复所有场景本质属性；

• 提出了SIRFS算法（可以看作是intrinsic image算法，不过shading是shape和Illumination的组合函数形成的，还可以被看作SFS但reflectance和illumination是未知的），首次完整的本质图像分解（将原图分解为reflectance，shape，Illumination）

许多这些本质图像算法的限制因素似乎是它们将shading视为一种图像，忽略了这样一个事实，即shading从结构上来说是某种形状和某种照明模型的产物。通过解决这个本质图像问题的超集，恢复shape和Illumination而不是shading，我们的模型产生了比任何本质图像方法更好的结果。

SIRFS问题公式化：
\[ \begin{array}{ll}{\underset{R, Z, L}{\operatorname{maximize}}} & {P(R) P(Z) P(L)} \\ {\text { subject to }} & {I=R+S(Z, L)}\end{array} \]
其中\(R\)为log-reflectance image，\(Z\)为depth-map，\(L\)为球面谐波Illumination向量。\(S(Z, L)\)是一个渲染引擎，它的作用是将\(Z\)线性化一组表面法线，然后通过这些表面法线和L构成log-shading，\(P(R), P(Z), P(L)\)分别是reflectance, shape和illumination的先验，SIRFS算法就是要在重构约束下，最大化三个先验的似然概率。

进一步化简，将最大化问题转化成最小化问题，取负对数，然后根据重构约束，可以将最大化似然概率转为如下公式，去除了R这个自由未知量。
\[ \underset{Z, L}{\operatorname{minimize}} \quad g(I-S(Z, L))+f(Z)+h(L) \]
反射先验

三种先验：Smoothness，Parsimony，Absolute Reflectance。

Smoothness：自然图像的反射图趋向于分段连续，这等效于反射图的变化趋向小而稀疏，作者在灰度反射平滑使用一个多元高斯尺度混合(GSM)，将每个反射率像素与其相邻像素之间的差值叠加在一起，在这个模型下使R的可能性最大化，它对应于最小化下面的cost函数：
\[ g_{s}(R)=\sum_{i} \sum_{j \in N(i)} c\left(R_{i}-R_{j} ; \boldsymbol{\alpha}_{R}, \boldsymbol{\sigma}_{R}\right) \]
其中\(R_i - R_j\)为从像素\(i\)到像素\(j\)的\(log-RGB\)的差异, \(N(i)\)是围绕i领域为5的区域，\(c(\cdot ; \alpha, \sigma)\)为离散单变量的负对数似然混合高斯尺度，\(\alpha\)和\(\sigma\)为参数，公式如下：
\[ c(x ; \boldsymbol{\alpha}, \boldsymbol{\sigma})=-\log \sum_{j=1}^{M} \alpha_{j} \mathcal{N}\left(x ; 0, \sigma_{j}^{2}\right) \]
反射率图像最可能是平的，所以设定GSM的均值为0.

高斯尺度混合模型以前曾被用于模拟自然图像中的重尾分布，用于去噪或图像修复。同样地，使用这个分布族给我们一个对数似然，它看起来像一个光滑的，重尾样条曲线，从0开始单调地递减。反射率变化的代价随变化幅度的增大而增大，但由于分布具有较重的尾部，小变化的影响是最强烈的（对应于shading的变化），大变化的影响是最微弱的。这与希望反射图大部分是平的，但偶尔变化很大吻合。（这句话不太懂）

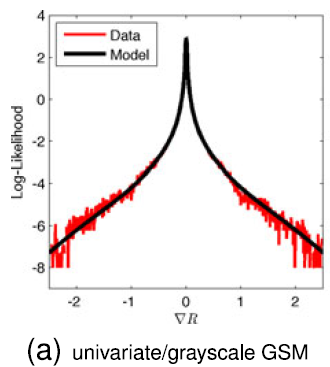
Parsimony

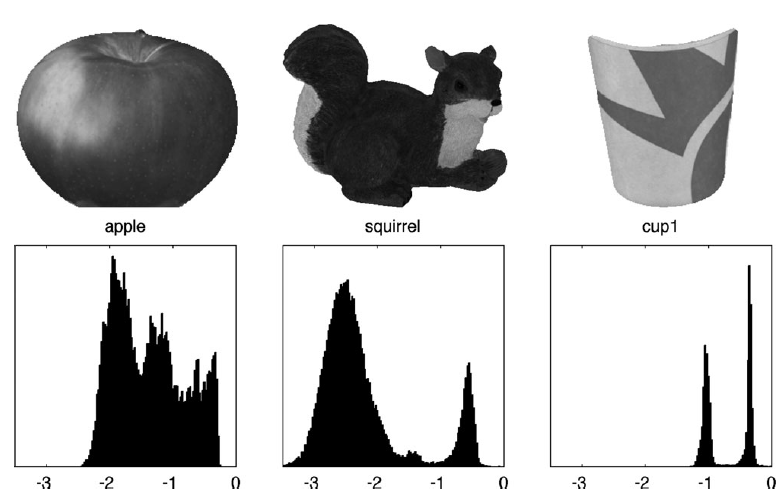
对反射率图像的期望是，在一张图像中有少量反射率，即用于绘制图像的调色板是小的。作者展示了数据集中三个对象的灰度对数反射率的边缘分布。虽然人造的cup1物体在其分布上表现出最明显的峰顶，但像apple这样的自然物体却表现出明显的集群性。因此，我们将构建一个鼓励节俭的先验——即我们对场景反射率的表示是经济和有效的，或“稀疏的”。

只使用一个平滑的先验，如在a，允许反射率变化在不连通区域。在b中，只使用节俭的先验，鼓励反射率取少量的值，但不鼓励它形成大的分段常数区域。只有把这两个先验结合起来使用，如c我们的模型是否正确地支持正常的、类似于油漆的棋盘配置。这证明了我们对反射率的光滑性和节俭先验的重要性。

利用二次熵公式，使对数反射率的熵最小，从而鼓励节俭，公式如下：
\[ \begin{aligned} g_{e}(R) &=-\log \left(\frac{1}{Z} \sum_{i=1}^{N} \sum_{j=1}^{N} \exp \left(-\frac{\left(R_{i}-R_{j}\right)^{2}}{4 \sigma_{R}^{2}}\right)\right) \\ Z &=N^{2} \sqrt{4 \pi \sigma^{2}} \end{aligned} \]
Absolute Reflectance

没有绝对先验，我们的模型将乐于将图像中的灰色像素解释为在灰色照明下的灰色反射，或者像在极亮照明下的近似黑色反射，或者在黄色照明下的蓝色反射，等等。

绝对先验对于颜色恒常性是基本的，因为大多数基本的白平衡或自动对比度/亮度算法都可以被看作是将类似的成本最小化：灰色世界假设对非灰色的反射率进行惩罚，白色世界假设对非白色的反射率进行惩罚，基于色差的模型对位于以前可见反射率范围之外的反射率进行惩罚。

先验公式：
\[ \underset{\mathbf{f}}{\operatorname{minimize}} \quad \mathbf{f}^{\mathrm{T}} \mathbf{n}+\log \left(\sum_{i} \exp \left(-\mathbf{f}_{i}\right)\right)+\lambda \sqrt{\left(\mathbf{f}^{\prime \prime}\right)^{2}+\epsilon^{2}} \]
\(f\)是我们的样条曲线，它决定了分配给每个反射率的非标准化负对数似然，\(n\)为对数反射率的一维直方图，\(\mathbf{f}^{\prime \prime}\)是样条函数的二阶偏导，\(\epsilon\)确保先验公式可微。

形状先验

三种先验：Smoothness，Surface Isotropy，The Occluding Contour。

Smoothness

平滑度的假设是基于形状很少弯曲，通过最小化平均曲率的变化来建立模型。

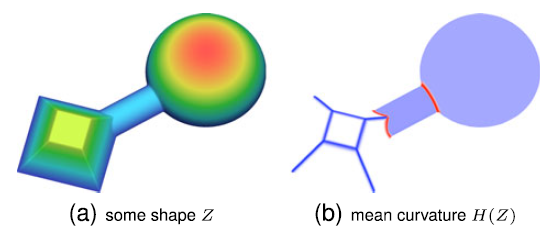
上面图形是形状及其平均曲率的可视化(蓝色=正，红色=负，白色= 0)。平面和肥皂膜的平均曲率为0，球体和圆柱体的平均曲率为常数，形状弯曲时平均曲率变化。

平均曲率的计算公式如下：
\[ H(Z)=\frac{\left(1+Z_{x}^{2}\right) Z_{y y}-2 Z_{x} Z_{y} Z_{x y}+\left(1+Z_{y}^{2}\right) Z_{x x}}{2\left(1+Z_{x}^{2}+Z_{y}^{2}\right)^{3 / 2}} \]
对形状的平滑先验是一个高斯尺度的混合对Z的平均曲率的局部变化：
\[ f_{k}(Z)=\sum_{i} \sum_{j \in N(i)} c\left(H(Z)_{i}-H(Z)_{j} ; \boldsymbol{\alpha}_{k}, \boldsymbol{\sigma}_{k}\right) \]
公式与反射图的平滑先验一致。

Surface Isotropy

我们假设形状的表面是各向同性的——同样可能面向任何方向，比如在球体中。然而，观察各向同性形状会产生偏差，因为观察到的表面更可能面向观察者，而不是垂直于观察者(如下图a中放置在球体上的红色标尺图形图钉所示)。我们通过在\(N^z\)上施加先验来消除这种偏差，如下图b所示，它粗略地类似于我们的训练数据

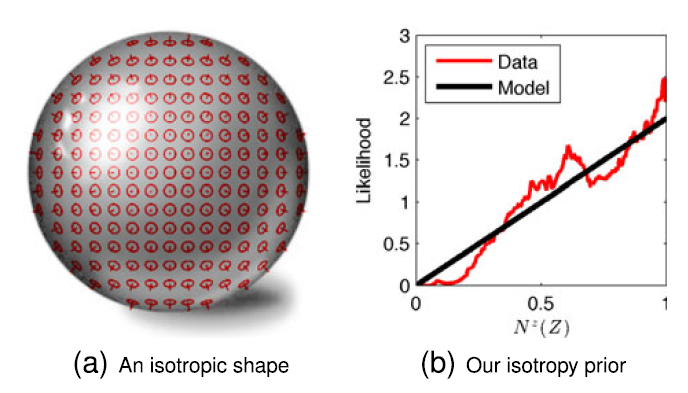
表面各向同性先验的公式如下：
\[ f_{i}(Z)=-\sum_{x, y} \log \left(N_{x, y}^{z}(Z)\right) \]
\(N_{x, y}^{z}(Z)\)是Z的表面法线在位置\((x,y)\)上的\(z\)分量.

The Occluding Contour

形状的遮挡轮廓(包围形状轮廓的轮廓)是一种强大的形状解释线索，它通常控制shading线索，并提出了算法来粗略估计给定轮廓信息的形状.

在物体的遮挡轮廓上，表面与所有有利位置的光线相切。在正交投影下(我们假设)，这意味着法线的z分量为0,x和y分量由图像中的轮廓决定。表面的闭合轮廓往往由分支(表面从有利位置与光线相切的点，如圆柱体的光滑面)和边缘(表面的突然不连续，如圆柱体的顶部或一张纸的边缘)组成.

我们提出了分支先验的“软”版本，它捕捉了我们期望看到的类似“分支”的行为，但是它可能被边缘或小分支违反。
\[ f_{c}(Z)=\sum_{i \in C}\left(1-\left(N_{i}^{x}(Z) n_{i}^{x}+N_{i}^{y}(Z) n_{i}^{y}\right)\right)^{\gamma_{c}} \]
该杯的侧面是“分支”，即表面法线面向外并垂直于闭合轮廓