问题描述:
假设有有一个含有N个长整型元素的数组。已知其中有若干个数出现了n次,除了一个数只出现了m次(0<m<n)。设计一个复杂度为O(n)的算法,且只多用O(1)的内存,找出出现m次的这个数。
解决思路:
这个问题可以看成,在数组中,找出唯一的一个出现次数与其他数不都同的元素。初步设想可以设计一个计数器来记录各个数出现的次数,最终只返回那个与其他数出现次数不同的那个数。这可以通过设定一个条件判断来实现,当计数器记录的某个次数达n次时就清零,只出现m次(m<n)的那个数就被保留下来。
关键是怎么在无序的列表中只遍历一次就能统计出各个数出现的次数。这可以通过巧妙地运用一个按位运算来实现。首先,把每个数看作一个放在64位的计数器里(count[64])的二进制数。然后,设定一个按位运算规则。在一次遍历过程中,对每一个数的每一位都与1(相当于掩码)按位与,如果结果为1(即表示该位数是1),则该位的计数器(count[j])+1,当计数器累加至n时,计数器清零。经过一次完整遍历后,把各个数的每一位1都按位累加,计数器满n则清零,相当于把每个出现n次的数都清零了,留下的则是出现m次(m<n)的那个数,其每一位1都累加了m次。最后,把累加的结果转换为原来的数,采用的办法是把累加结果的非0位通过与1按位或运算置1。
具体的实现代码如下:
1 #include<iostream> 2 using namespace std; 3 4 int main(int argc, char const *argv[]) 5 { 6 /* 7 问题描述: 8 有一个数组有N个整数,其中若干个数都出现了n次,只有一个数只出现了m次(0<m<n)。设计一个算法,时间复杂度O(N)且只用O(1)的多余空间。 9 */ 10 11 int const num = 64; //64位系统的长整形数的位数 12 int N=21; //数组中的元素总数 13 int a[21] ={2,5,5,5,2,321,321,5,1,1,321,1,5,321,1,2,1,5,1,321,321}; 14 int n = 6, m=3; // 若干个数出现n次,仅一个数出现m次 15 int count[num]; //64位计数器(64位系统的长整形数的位数);记录每一位1的个数,a中整数应<2^23 16 17 int i; 18 19 //初始化计数器为0 20 for (i = 0; i < num; i++) 21 { 22 count[i] = 0; 23 } 24 25 //把各个数的每一位1都按位累加,计数器满n则清零,相当于把每个出现n次的数都清零了,留下的则是出现m次(m<n)的那个数,其每一位1都累加了m次 26 for (i = 0 ; i < N; i++) 27 { 28 for (int j = 0 ; j < num ;j++) 29 { 30 if ((a[i] >> j) & 0x1) //把第j位移到最右一位,取最后一位,具体方法是吧a[i]右移j位后与0x1(掩码)与,由此判断第j位是否为1 31 count[j]++; 32 33 if(count[j] == n) //计数满n就清零 34 count[j] = 0; 35 } 36 37 } 38 39 //把累加m次后的结果转换为原来的数 40 int result = 0; 41 for(int j = 0; j < num; j++) 42 { 43 if(count[j]) //如果第j位的计数器非0 44 result = result | (0x1 << j) ; //把非零的第j为数置1 45 } 46 47 //输出结果 48 cout<<"result:"<<result<<endl; 49 50 return 0; 51 }
测试结果:
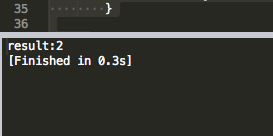







 本文介绍了一种在数组中寻找出现次数不同于其他元素的特殊元素的方法。该方法利用位运算技巧,仅使用O(1)的空间复杂度及O(n)的时间复杂度完成任务。适用于64位长整型数组。
本文介绍了一种在数组中寻找出现次数不同于其他元素的特殊元素的方法。该方法利用位运算技巧,仅使用O(1)的空间复杂度及O(n)的时间复杂度完成任务。适用于64位长整型数组。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








