1、注意力模型的直观理解
我们以前用过这种Seq2Seq的编码解码架构(a Encoder-Decoder architecture)来完成机器翻译的任务。当使用RNN读入一个句子时候,另一个就会输出一个句子。这种模型对于短句子有用,但是长句子却效果不好。如图:
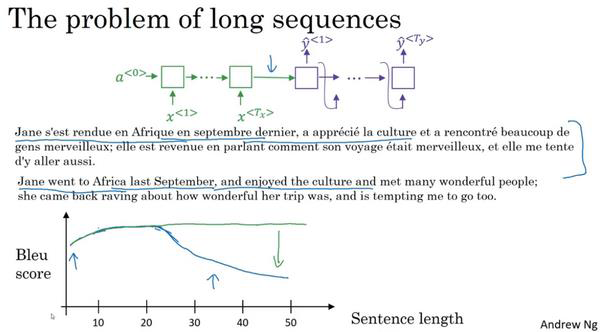
可以看到随着句子长度增长,Bleu Score在下降。因为上面的模型要记住一整个很长的法语句子,然后在Decoder中输出。而人工翻译可以先翻译出句子的部分,再看下一部分,并翻译一部分,就这样一直下去,因为记忆整个句子是很难的。所以,我们引入了注意力模型(the attention model),如图所示:
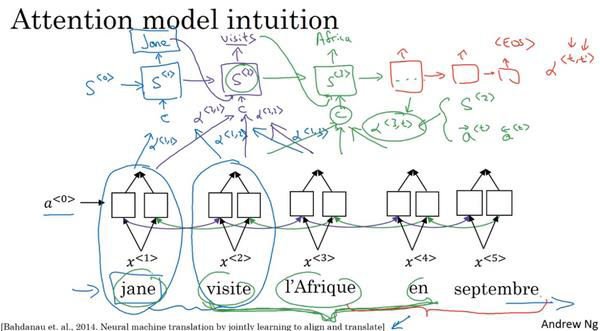
注意力模型来自于Dimitri, Bahdanau, Camcrun Cho, Yoshe Bengio。(Bahdanau D, Cho K, Bengio Y. Neural Machine Translation by Jointly Learning to Align and Translate[J]. Computer Science, 2014.)。
让我们来举例说明一下。假如我们有一个法语句子:(法语)Jane visite l'Afrique en Septembre。假定我们使用RNN,在这种情况下,我们可以使用一个双向RNN(a bidirectional RNN),为了计算每个输入单词的特征集(set of features),你必须要理解输出 到
到 一直到
一直到 的双向RNN。但是我们并不是只翻译一个单词,让我们先去掉上面的
的双向RNN。但是我们并不是只翻译一个单词,让我们先去掉上面的 ,就用双向的RNN。我们将使用另一个RNN生成英文翻译。我们用
,就用双向的RNN。我们将使用另一个RNN生成英文翻译。我们用 表示RNN(也就是解码器Decoder)的隐层状态(the hidden state in this RNN)。我们希望在这个模型里第一个生成的单词是Jane。于是等式就是,当你尝试生成第一个词时候,我们应该看输入的法语句子的哪个部分。所以,注意力模型就会计算注意力权重。我们用
表示RNN(也就是解码器Decoder)的隐层状态(the hidden state in this RNN)。我们希望在这个模型里第一个生成的单词是Jane。于是等式就是,当你尝试生成第一个词时候,我们应该看输入的法语句子的哪个部分。所以,注意力模型就会计算注意力权重。我们用 来表示当你生成第一个词时你应该放多少注意力在输入的第一个词上。然后我们算第二个,
来表示当你生成第一个词时你应该放多少注意力在输入的第一个词上。然后我们算第二个, 表示我们计算第一个词Jane时,我们将会放多少注意力在输入的第二个词上面,后面同理。这些将会告诉我们,我们应该花多少注意力在记号为
表示我们计算第一个词Jane时,我们将会放多少注意力在输入的第二个词上面,后面同理。这些将会告诉我们,我们应该花多少注意力在记号为 的内容上。这是最上面RNN(也就是解码器Decoder)的一个单元,如何尝试生成第一个此。对于RNN的第二步,我们将有一个新的隐藏状态
的内容上。这是最上面RNN(也就是解码器Decoder)的一个单元,如何尝试生成第一个此。对于RNN的第二步,我们将有一个新的隐藏状态 ,我们也会用一个新的注意力权值集,我们将用
,我们也会用一个新的注意力权值集,我们将用 告诉我们生成第二个词visits时,我们将会放多少注意力在输入的第一个词上面,后面同理。最后直到结束。
告诉我们生成第二个词visits时,我们将会放多少注意力在输入的第一个词上面,后面同理。最后直到结束。
2、注意力模型(Attention Model)
我们先记住这些符号的意义: 表示是双向RNN已经计算了的前向和后向的特征值,
表示是双向RNN已经计算了的前向和后向的特征值, 表示Decoder的第几个隐层状态,
表示Decoder的第几个隐层状态, 表示对于第
表示对于第 个输出我们关注第
个输出我们关注第 个输入(注意力权重集),
个输入(注意力权重集), 表示Decoder第几个输出。上面我们看到,注意力模型翻译句子时,只注意到一部分的输入句子,更像人类翻译。如下图所示的注意力模型:
表示Decoder第几个输出。上面我们看到,注意力模型翻译句子时,只注意到一部分的输入句子,更像人类翻译。如下图所示的注意力模型:
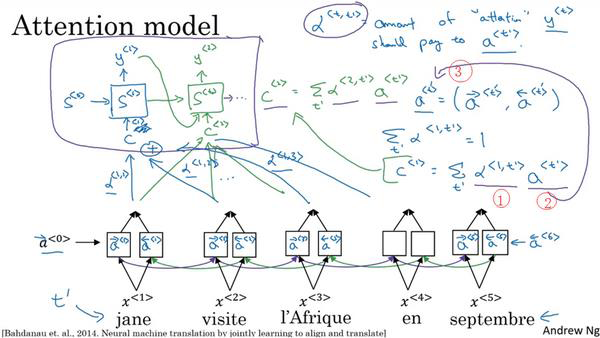
我们假定有一个句子,并使用双向RNN,去计算每个词的特征。这里的这项(上图编号1所示)就是注意力权重,这里的这项(上图编号2)来自于这里(上图编号3)。于是,当你在 处生成输出词,你应该花多少注意力在第
处生成输出词,你应该花多少注意力在第 个输入词上面,这是生成输出的其中一步,其他的类似。
个输入词上面,这是生成输出的其中一步,其他的类似。
底层是一个双向RNN,需要处理的序列作为它的输入。改该网络中每一个时间步的激活 中,都包含前向传播和后向传播的激活:
中,都包含前向传播和后向传播的激活:
顶层是一个“多对多”结构的RNN,第 步该网络前一个时间步的激活
步该网络前一个时间步的激活 、输出
、输出 以及底层的BRNN中多个时间步的激活
以及底层的BRNN中多个时间步的激活 作为输入。对第
作为输入。对第 个时间步的输入
个时间步的输入 有:
有:
其中参数 意味着顶层RNN中,第
意味着顶层RNN中,第 个时间步输出
个时间步输出 中,把多少注意力放在了底层BRNN的第
中,把多少注意力放在了底层BRNN的第 个时间步的激活
个时间步的激活 上。它总有:
上。它总有:
为了确保参数 满足上式,常用Softmax单元来计算顶层RNN的第
满足上式,常用Softmax单元来计算顶层RNN的第 个时间步对底层BRNN的第
个时间步对底层BRNN的第 个时间步的激活的注意力:
个时间步的激活的注意力:
其中的 由顶层RNN的激活
由顶层RNN的激活 和底层BRNN的几乎
和底层BRNN的几乎 一起输入一个隐层中得到的。
一起输入一个隐层中得到的。
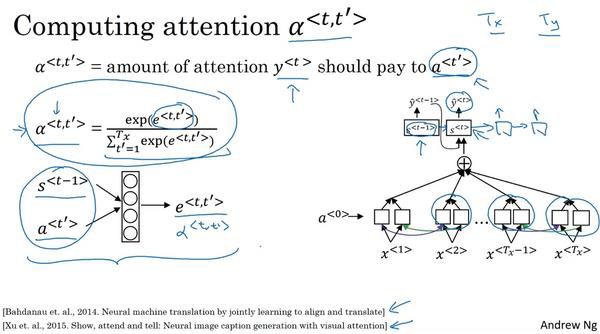
在无法获知 、
、 和
和 之间的关系的时候,就用上图所示的神经网络进行学习。
之间的关系的时候,就用上图所示的神经网络进行学习。





















 467
467

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








