【杂题总汇】AGC027 C - ABland Yard-优快云博客

本文详细解析了AGC027竞赛C题，通过巧妙的图论和二分图应用，解决了一个关于无向图中寻找特定环的问题。关键在于理解如何通过拆点思想将原问题转化为在二分图中寻找环，从而判断所有可能的字符串组合是否都能由图中的路径表示。

◆AGC027◆C - ABland Yard

终于知道为什么比赛的时候这么多人做C题了……

+传送门+（这是beta版的）

◇ 题目（自己翻译的，不要在意细节……）

P.S. (@ 2018-9-22) 抱歉……隔了一天写博客，精神不太正常……把题面和题解放反了，这是C题的题解，B题的题解另外再写一篇?

·【描述】

给出一个N个点、M条边的无向图（节点编号1~N）。每个节点有一个值'A'或'B'，你可以从任意一个节点出发，经过一些节点后（可以重复经过），你将经过的节点的值顺次写出来，就可以得到一个只包含'A'或'B'的字符串。求对于只包含'A'或'B'的字符串S都找得到一个合法的访问序列使得得到的字符串恰好为S。

·【输入】

第一行为N,M。

第二行为一个字符串，第i个字符表示节点i的值（1开始）。

接下来M行每行描述一条边，格式为该边的两端点。

·【输出】

是否满足上述条件。

◇ 解析

表面上其实看不出来这是一道结论题……

最重要的一个结论应该是只要找到一个"AA"，"BB" 相间的环就满足问题。可以用反证法：

①若环内连续A或B的个数小于1，则无法构成"AA"或者"BB"；

②若环内连续A或B的个数超过2(>)，则必然存在一个串，结尾为"ABBA"或"BAAB"无法构成；

so that? 其实已经得证了……

如何找满足条件的环？我们可以想象环是长这个样子的：

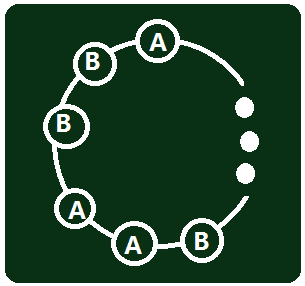
然后我们就会发现……除了用点集表示一个环，也可以用边集。

我们可以令连接"AA"或"BB"的边为0，连接"AB"的边为1（QwQ）。所以环就是10101010101……所以对于环上一个点，它在环上的两条边一定是一条1、一条0。

简单地，用DFS，从一个点出发，先走一条"1"边，再走一条"0"边，交替进行（或者先"0"边，然后"1"边）。非常的麻烦，并不想这么做。于是运用拆点的思想，将一个点u拆一个虚点u'。原图有多条边以点u开始，令原图中边的结束点为v，当u,v标志相同时则我们将u连接v'，v连接u'，否则将u'连到v，v'连到u（单向）。

举个例子：

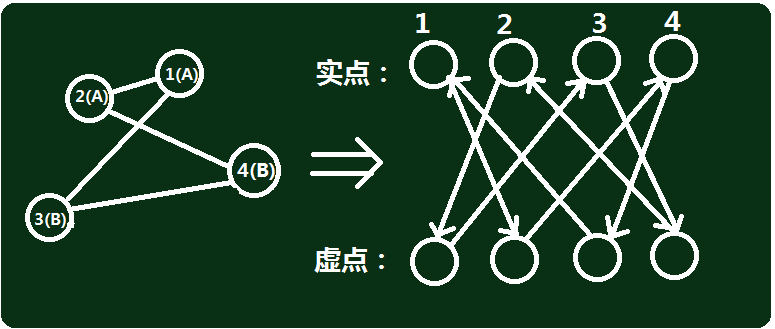
（有点乱不要在意TAT）

解释一下建图过程：拿点1来说

由于1->2是连接相同标志点的边（"0"边），则建立 1->2' 和 2->1'；由于 1->3 是连接不同标志点的边（"1"边），则建立 1'->3 和 3'->1 。其他都是这样建的。二分图吗？right！

环 1->2->4->3->1 就是一个合法环，那么在新建的图上是怎样表现的？ 1->2'->4->3'->1 ，二分图上找一个环？就是这样。用二分图，我们可以直接回避连续经过"1"边或"0"边，因为从实点出发到虚点，就会经过"0"边，而从虚点到实点就会经过"1"边，二分图上实点虚点交替经过。只要在二分图上找到一个环即可。

◇ 源代码

/*Lucky_Glass*/
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
using namespace std;
const int N=int(2e5);
vector<int> lnk[2*N+5];
int n,m;
char fla[N+5];
int tag[2*N+5];
void DFS(int u){
	tag[u]=1;
	for(int i=0;i<lnk[u].size();i++){
		int v=lnk[u][i];
		if(tag[v]==0)
			DFS(v);
		if(tag[v]==1){
			printf("Yes\n");
			exit(0);
		}
	}
	tag[u]=-1;
}
int main(){
	scanf("%d%d%s",&n,&m,fla+1);
	for(int i=0;i<m;i++){
		int u,v;scanf("%d%d",&u,&v);
		if(fla[u]==fla[v]){
			lnk[u].push_back(v+n);
			lnk[v].push_back(u+n);
		}
		else{
			lnk[u+n].push_back(v);
			lnk[v+n].push_back(u);
		}
	}
	for(int i=1;i<=n;i++)
		if(tag[i]==0)
			DFS(i);
	printf("No\n");
	return 0;
}