凤翔中学2018届高三文科数学高考模拟试卷细目表

凤翔中学2017-2018学年度高三文科数学高考冲刺模拟试题01细目表

题号	分级考点	题型和方法
选择题01	集合-集合的关系	由集合的关系确定集合的元素
选择题02	复数-复数的乘除运算	复数的乘除运算及复数与点的对应性
选择题03	常用逻辑用语-充要条件	充要条件的判断，不等式性质，指数对数运算
选择题04	立体几何-三视图	已知三视图的体积，确定三视图中的相关数量
选择题05	数列-等差等比数列的综合	由等差、等比数列的性质的综合应用求数列中的某一项
选择题06	不等式-线性规划	给定可行域，求目标函数的最小值
选择题07	概率-古典概型	古典概型的概率计算
选择题08	三角函数-三角函数的变形和性质	变形为正弦型函数后，考查其各种性质
选择题09	立体几何-多面体的体积	正方体内部所接的八面体的体积计算
选择题10	函数与导数-导数的应用	给定函数的单调性，求参数的取值范围或最大值
选择题11	解析几何-双曲线的性质	给定双曲线的相关量，求双曲线的离心率
选择题12	函数-函数性质的综合应用	利用函数的性质推导单调性，并借助单调性比较大小
填空题13	平面向量-向量的垂直计算	由两个平面向量的垂直求解参数的值
填空题14	数列-等比数列	等比数列的性质和对数的综合运算求值
填空题15	函数-函数与方程	给定两个函数，求解其函数方程的根的个数
填空题16	解析几何-抛物线	给定抛物线的相关量，求某个角的最大值
解答题17	三角函数-解三角形	利用正余弦定理解三角形，①求角；②求边
解答题18	立体几何-空间几何体的位置关系	①求证面面垂直；②求多面体的体积
解答题19	概率与统计-统计	①茎叶图制作，求众数和中位数；②古典概型的概率计算
解答题20	解析几何-椭圆、圆与直线	①求椭圆的方程；②求三角形面积最大时的最大值点或直线方程
解答题21	函数与导数-导数的意义及应用	①利用导数几何意义求参数的值；②求函数的单调区间和极值点
选做题22	坐标系与参数方程	①极坐标方程和参数方程化普通方程；②求圆上动点到直线的距离的最小值
选做题23	不等式选讲	①已知绝对值不等式恒成立，求参数的取值范围；②解绝对值不等式

其中代数部分的难点题目：

• 第3题，主要验证\(x>1\)能否相互推出\(ln2^x>1\)。用不等式的性质和函数的性质。

• 第5题，主要考查学生，不用\(S_n=\cfrac{a_1(1-q^n)}{1-q}\)的公式，而是使用定义式\(S_n=a_1+a_2+\cdots+a_n\)代入运算，简单快捷。

• 第8题，第三个选项的简单解法，当得到\(f(x)=sin(2x+\cfrac{\pi}{3})-\cfrac{\sqrt{3}}{2}\)时，判断单调性时，学生一般是令\(2k\pi+\cfrac{\pi}{2}\leq 2x+\cfrac{\pi}{3}\leq 2k\pi+\cfrac{3\pi}{2}(k\in Z)\)，给\(k\)赋值，求得函数\(f(x)\)在区间\([\cfrac{\pi}{12}，\cfrac{7\pi}{12}]\)上单调递减，快速的做法是由\(\cfrac{\pi}{12}\leq x\leq \cfrac{7\pi}{12}\)，求得\(\cfrac{\pi}{2}\leq 2x+\cfrac{\pi}{3}\leq \cfrac{3\pi}{2}\)，从而得到函数在区间\([\cfrac{\pi}{12}，\cfrac{7\pi}{12}]\)上单调递减。

• 第10题，已知含参函数的单调性如单调递增，求参数的取值范围，常用的思路是\(f'(x)\ge 0\)恒成立，且\(a\)的值不能使函数\(f(x)\)成为常函数，所以常常需要将\(a\)代入原函数验证，不过大多题目我们观察就可以看出函数是否是常函数。转化为恒成立问题后，紧接着的做法往往是分离参数。本题容易出错的地方是错误的认为\(f'(x)>0\)恒成立，这样就可能漏解。

• 第12题，由\(f(x+1)=\cfrac{k}{f(x)}(k\neq 0)\)也能推出\(T=2\)，\(a=f(log_{0.5}2)=f(log_{2^{-1}\;^{2^1}})=f(\frac{1}{-1}log_22)=f(-1)=f(1)\)，\(c=f(2^{0.5})=f(\sqrt{2})=f(1.4)=f(1.4-2)=f(-0.6)=f(0.6)\)。

• 第15题，注意函数\(g(x)=|log_3(x-1)|\)的图像做法，其中一个做法次序是\(y=log_3x\)，再做\(y=|log_3x|\)，再做\(y=|log_3(x-1)|\)的图像。

• 第21题(1)中，注意挖掘题目的隐含条件，\(f'(2)=0\)且\(f(2)=8\)，(2)中注意将结果写成区间，但是不要用并集符号，还有极值点不是点，不要写成点的坐标形式。

• 第22题(2)中，法1：平面几何法；法2：三角函数+圆的参数方程法；法3：平行线法。

凤翔中学2017-2018学年度高三文科数学高考冲刺模拟试题02细目表

题号	分级考点	题型和方法
选择题01	集合-集合的表示	用列举法表示有限集合
选择题02	复数-复数的共轭复数	复数的乘除运算及复数的共轭复数概念
选择题03	立体几何-平面向量	给定向量的相关关系，求向量的模的最大值
选择题04	不等式-大小比较	涉及指数、对数、幂的大小比较
选择题05	常用逻辑用语-复合命题真假判断	给定复合命题的真假，求参数的取值范围
选择题06	立体几何-三视图	给定三视图，求实物几何体的体积的比值
选择题07	数列-等差等比综合	给定等差等比数列综合，求等差数列的前几项和
选择题08	不等式-二次不等式恒成立	给定二次不等式恒成立，求参数的取值范围
选择题09	算法与框图-程序框图	求算法的执行结果
选择题10	解析几何-双曲线和圆	给定双曲线的离心率的范围，求其渐近线和圆的交点个数
选择题11	立体几何-三棱锥	给定折叠而成的三棱锥，求其外接球的表面积
选择题12	函数-抽象函数不等式的求解	利用导数构造抽象函数，从而求解抽象函数不等式，难点题目
填空题13	三角函数-三角函数定义	用三角函数的定义求解角的大小
填空题14	概率-几何概型	考查长度型几何概型
填空题15	解析几何-抛物线	利用抛物线的性质求其中的线段长度
填空题16	函数-幂函数的定义性质	利用幂函数的定义和性质，求参数的值
解答题17	三角函数-解三角形	①利用三角变换求值；②求三角形面积的最大值
解答题18	概率与统计-统计	①求线性回归方程；②用线性回归方程预测变量的预报值
解答题19	立体几何-长方体	①给定线面平行，求证线段长的关系；②求三棱锥的体积
解答题20	解析几何-椭圆与直线	①求椭圆的标准方程；②探究性问题，比值是否为定值
解答题21	函数与导数-导数的意义及应用	①利用导数几何意义求切线方程；②求函数的单调区间；③不等式证明
选做题22	坐标系与参数方程	①极坐标方程和参数方程化普通方程；②求弦长度
选做题23	不等式选讲	①求解绝对值不等式；②绝对值不等式的证明

其中代数部分的难点题目：

• 第8题，若将题目改成对任意的实数\(x\in [2，3]\)，不等式\(x^2+mx+2m-3\ge 0\)恒成立，求实数\(m\)的取值范围，那么需要分类讨论求解或者分离参数求解。参见

• 第12题， 函数\(f(x)\)的导函数为\(f'(x)\)，若\(\forall x\in R\) 恒有\(f'(x)<f(x)\)成立，且\(f(2)=1\)，则不等式\(f(x)>e^{x-2}\)的解集为【】

A.\((-\infty，1)\;\;\;\;\;\;\) B.\((1，+\infty)\;\;\;\;\;\;\) C.\((2，+\infty)\;\;\;\;\;\;\) D.\((-\infty，2)\;\;\;\;\;\;\)

分析：涉及构造函数，难点题目，构造函数\(g(x)=\cfrac{f(x)}{e^x}\)，则\(g'(x)=\cfrac{f'(x)e^x-f(x)e^x}{(e^x)^2}=\cfrac{f'(x)-f(x)}{e^x}<0\)，能得到\(g(x)\)的单调性为单调递减，

且知道\(g(2)=\cfrac{1}{e^2}\)，这时候需要将所求解的不等式\(f(x)>e^{x-2}\)做适当转化，向\(g(x)\)靠拢。

即\(f(x)>\cfrac{e^x}{e^2}\)，同乘\(\cfrac{1}{e^x}\)，得到\(\cfrac{f(x)}{e^x}>\cfrac{1}{e^2}\)，即\(g(x)>g(2)\)，由单调递减得到\(x<2\)。故选D.

• 第13题，考查三角函数的定义和三角函数求值类中的给值求角。解法比较多，待后整理。

【题文】已知锐角\(\alpha\)终边上一点\(P(sin\cfrac{\pi}{5}，cos\cfrac{\pi}{5})\)，则\(\alpha\)的值为______。

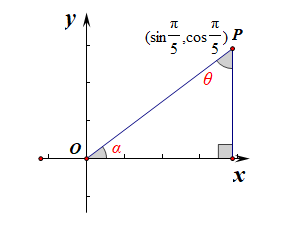
法1：如图所示，\(tan\theta=\cfrac{sin\frac{\pi}{5}}{cos\frac{\pi}{5}}=tan\cfrac{\pi}{5}\)，故\(\theta=\cfrac{\pi}{5}\)，则\(\alpha=\cfrac{\pi}{2}-\cfrac{\pi}{5}=\cfrac{3\pi}{10}\)；

法2：由图可知，\(|OP|=1\)，\(sin\theta=sin\cfrac{\pi}{5}\)，则\(cos\alpha=sin\theta=sin\cfrac{\pi}{5}=cos\cfrac{3\pi}{10}\)，故\(\alpha=\cfrac{3\pi}{10}\)；

法3：见参考答案。

凤翔中学2017-2018学年度高三文科数学高考冲刺模拟试题03细目表

题号	分级考点	题型和方法
选择题01	集合-集合的关系	确定含参数的集合，并求其并集
选择题02	复数-复数相等和复数的模	用复数相等确定复数，并求复数的模
选择题03	常用逻辑用语-充要条件	判断充要条件，通过集合的关系判断命题的关系
选择题04	推理与证明-逻辑推理	用逻辑推理判断正误
选择题05	立体几何-三视图	给定三视图，求其对应几何体的外接球的表面积
选择题06	程序框图-分段函数方程	程序框图背景下的分段函数方程求解
选择题07	三角函数-三角函数化简和性质	将三角函数化简后考查其相应的性质
选择题08	立体几何-折叠形成的立体图形	立体图形的相关位置关系，相关性质等
选择题09	解析几何-双曲线和圆	给定双曲线的离心率，渐近线和圆所得弦长求参数的值
选择题10	不等式-均值不等式	利用导数给定整式型限定条件，求分式表达式的最小值
选择题11	解析几何-抛物线	有关抛物线的性质的相关求值
选择题12	三角函数-三角函数和导数的融合	三角变换和求导得到的新三角函数的性质的考查
填空题13	函数-函数的对称性	已知函数关于点对称，求参数的值
填空题14	函数-函数与导数	包含导数的函数解析式的确定或函数的导数值得确定
填空题15	不等式-均值不等式	向量形式给出的限定条件，求代数式的最小值
填空题16	函数-抽象函数	求解抽象函数不等式
解答题17	数列-数列的证明和求和	①等比数列的证明；②错位相减法求数列的和
解答题18	概率与统计-统计背景和古典概型	①求脱贫率比值；②分层抽样，列举法，古典概型
解答题19	立体几何-四棱锥	①线面平行的证明；②求点到平面的距离
解答题20	解析几何-椭圆	①求椭圆的标准方程；②探究性问题，两条直线的斜率之积是否为定值
解答题21	函数与导数-导数的意义及应用	①给定函数在点处的切线斜率，求参数的值；②已知函数的零点，求参数的取值范围
选做题22	坐标系与参数方程	①极坐标方程和参数方程化普通方程；②已知点线距的最小值，求参数的值
选做题23	不等式选讲	①求解绝对值不等式；②融合恒成立和能成立命题，求参数的取值范围

其中代数部分的难点题目：

• 第4题，正难则反；比如你不好判断丙说的是真话，那么你可以先假设他说的是假话，然后分析，其余一样。

• 第7题，要求解\(f(x_1+x_2)\)，我们大概能猜想本题目需要用到函数的对称性。我们先求解得到\(f(x)=2sin(2x+\cfrac{\pi}{6})\)，然后由\(0\leq x\leq \cfrac{\pi}{2}\)，得到\(\cfrac{\pi}{6}\leq 2x+\cfrac{\pi}{6}\leq \cfrac{7\pi}{6}\)，
  

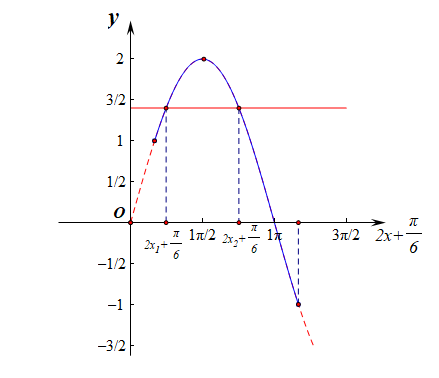
做出函数\(f(x)\)的大致图像，为了作图快捷，我们常常用\(2x+\cfrac{\pi}{6}\)作为横轴，如右图所示，

若要方程\(f(x)=m\)有两个不同的实根，需要两个函数的图像有两个不同的交点，此时必须有\(1\leq m<2\)，

这时我们设两个函数的图像的交点横坐标为\(2x_1+\cfrac{\pi}{6}\)和\(2x_2+\cfrac{\pi}{6}\)，则由图可知此时以\(2x+\cfrac{\pi}{6}\)为横轴的函数有对称轴\(x=\cfrac{\pi}{2}\)，

即\(\cfrac{2x_1+\cfrac{\pi}{6}+2x_2+\cfrac{\pi}{6}}{2}=\cfrac{\pi}{2}\)，化简为\(x_1+x_2=\cfrac{\pi}{3}\)，故\(f(\cfrac{\pi}{3})=2sin(\cfrac{2\pi}{3}+\cfrac{\pi}{6})=1\)。

• 第13题，难点一由函数图像关于点\((0，\cfrac{1}{2})\)，要求你必须能写出\(f(x)+f(-x)=1\)，难点二求解\(a\)的值时，可以用定义法详见参考答案，此时变形很复杂，且由\((a-1)[2^{2x}+(a-1)2^x+1]=0\)恒成立，故必须\(a-1=0\)，从而得到\(a=1\)；还可以用赋值法，比如\(f(0)+f(-0)=1\)，变形为\(\cfrac{2}{1+a}=1\)，得到\(a=1\)，当然这个方法要注意定义域。

• 第16题，偶函数不等式考查最多的是\(f(x)=f(-x)=f(|x|)\)。

• 第22题(2)，可以使用的方法比较多。

法1：平面几何法，详见参考答案；

法2：参数方程法，此时圆\(C_1\)上的动点\(P(\sqrt{2}cos\alpha，1+\sqrt{2}sin\alpha)\)，直线为\(x-y-t=0\)，

则点线距为\(d=\cfrac{|\sqrt{2}cos\alpha-1-\sqrt{2}sin\alpha-t|}{\sqrt{2}}=\cfrac{|2cos(\alpha+\cfrac{\pi}{4})-(t+1)|}{\sqrt{2}}\)，

当\(t+1\ge 0\)时，即\(t\ge -1\)时，\(d_{min}=\cfrac{|2\times(1)-(t+1)|}{\sqrt{2}}=2\sqrt{2}\)，

即\(|t-1|=4\)，解得\(t=5\)或\(t=-3\)(不符，舍去)

当\(t+1\leq 0\)时，即\(t<-1\)时，\(d_{min}=\cfrac{|2\times(-1)-(t+1)|}{\sqrt{2}}=2\sqrt{2}\)

即\(|t+3|=4\)，解得\(t=-7\)或\(t=1\)(不符，舍去)

法3：平行线法，由于直线\(C_2\)中已经有了一个参变数\(t\)，再重新引入另外一个比如\(m\)，会使得问题复杂的多，故这个方法我们在此题目中一般会回避的。

凤翔中学2017-2018学年度高三文科数学高考冲刺模拟试题04细目表

题号	分级考点	题型和方法
选择题01	复数-复数的运算和复数的模	用复数的乘除运算化简复数，并求其模
选择题02	函数-函数的定义域	解对数不等式求解函数的自然定义域
选择题03	常用逻辑用语-命题的否定形式	全称命题的否定形式
选择题04	函数-函数性质的综合应用	用函数的性质求周期函数的值
选择题05	向量-向量的投影	向量的分解或者向量在某个向量方向上的投影
选择题06	函数-函数图像的识别	通过解方程得到函数解析式，然后识别函数的图像
选择题07	三角函数-三角函数性质	正余弦函数性质应用于大小比较
选择题08	立体几何-三视图	三视图还原为后的几何体的体积
选择题09	函数-分段函数的奇偶性应用	利用分段函数的奇偶性求值
选择题10	不等式-均值不等式	利用函数恒过定点和点在直线上给定整式型限定条件，求分式表达式的最小值
选择题11	数学文化-算筹的理解	理解并能应用算筹来表达数学式
选择题12	解析几何-椭圆内的三角形面积	以椭圆为背景考查三角形面积的最大值
填空题13	三角函数-三角函数的求值	三角函数的给值求值类运算
填空题14	解析几何-双曲线、抛物线	求双曲线的离心率
填空题15	不等式-线性规划	给定线性约束条件，求斜率型的最大值
填空题16	立体几何-四面体	求几何体的外接球的体积
解答题17	数列-数列的通项公式和其应用	①数列的通项公式的求解；②利用数列的通项公式解方程
解答题18	立体几何-折叠成的几何体的计算	①求三棱锥中的线段比值；②三棱锥中的点面距
解答题19	统计-统计案例	①频率分布直方图和总体的估计；②2x2列联表，独立性检验
解答题20	解析几何-抛物线	①求直线的方程；②给定四边形面积，求直线的方程
解答题21	函数与导数-导数的意义及应用	①求常系数函数的极值；②探究性问题，是否存在实数，使得函数为单调函数
选做题22	坐标系与参数方程	①伸缩变化，以及转化为直角坐标方程；②求点到直线的距离的最小值
选做题23	不等式选讲	①求解绝对值不等式；②已知不等式的解集确定参数的值，均值不等式

其中代数部分的难点题目：

• 第7题，由\(a>b\)，能得出\(A>B(大边对大角)\)；能得出\(sinA>sinB(正弦定理)\)；能得出\(cosA<cosB(余弦函数单调性)\)；

• 第10题，注意限定条件的给出方式。

• 第15题，注意斜率型的引申，其他情形

• 第21题(2)，导函数或者导函数的分子是二次函数的，常常借助二次函数的图像简化思考。

比如，\(f'(x)=2x-(2-m)+\cfrac{m(1-m)}{x}=\cfrac{2x^2-(2-m)x+m(1-m)}{x}=\cfrac{(2x-m)(x+m-1)}{x}\)，

此时只需要关注导函数的分子函数\(g(x)=(2x-m)(x+m-1)\)，其有两个零点\(x=\cfrac{m}{2}\)和\(x=1-m\)，图像为抛物线的一部分，由于定义域是\((0，+\infty)\)

开口向上，结合图像我们可以判断，函数在\((1，+\infty)\)上只有单调递增，没有递减的可能；

若零点\(1-m>1\)，即\(m<0\)时，导函数在区间\((1，+\infty)\)上必然有正有负，故不会单调递增，

若零点\(\cfrac{m}{2}>1\)，即\(m>2\)时，导函数在区间\((1，+\infty)\)上必然有正有负，故不会单调递增，

接下来，我们其实只需要讨论\(m\in [0，2]\)上的情形就可以了。其余解答见参考答案即可。

凤翔中学2017-2018学年度高三文科数学高考冲刺模拟试题05细目表

题号	分级考点	题型和方法
选择题01	集合-集合的运算与表示	集合的运算及用韦恩图表示集合
选择题02	复数-复数的运算及模	$i$的运算的周期性，复数的模
选择题03	向量-向量的运算	已知向量的垂直求参数的值
选择题04	函数-函数与导数	用导数的几何意义解释函数的增长率
选择题05	常用逻辑用语-命题的真假判断	四种命题，命题的否定，复合命题等的判断
选择题06	数列-数学文化给定的数列问题	数学文化给定的等比数列的和求首项
选择题07	不等式-不等式性质，函数性质	不等式大小比较
选择题08	函数-映射概念考查	考查对映射概念的理解
选择题09	立体几何-三视图	三视图还原，求其体积
选择题10	立体几何-六棱锥外接球	求六棱锥的外接球的体积
选择题11	数列-数列性质的应用	由等差数列给出方程的系数，从而判断方程的根的情况
选择题12	解析几何-抛物线和圆	求所涉及的两个距离和的最小值
填空题13	函数-函数的导数	已知函数的极值点，求参数的值
填空题14	函数-函数的性质的应用	由函数的性质和给定值求函数的值
填空题15	解析几何-双曲线	求双曲线的离心率的取值范围
填空题16	函数-分段函数+周期+平移	利用函数的性质，用迭代法求函数的值
解答题17	三角函数-解三角形	①给值求角的大小；②已知三角形面积，求某一边的最小值
解答题18	立体几何-几何体的位置关系和相关计算	①求整面面垂直；②已知三棱锥的体积，求某条线段长
解答题19	统计-统计和概率	①完成频率分布表；②频率估计和概率计算；③求频率分布表的平均值
解答题20	解析几何-椭圆	①求椭圆的标准方程；②由线段的位置关系求解线段的比值
解答题21	函数与导数-导数的意义及应用	①已知函数的单调性，求参数的取值范围；②求函数在给定区间上的最值
选做题22	坐标系与参数方程	①化为参数方程和参数方程消参；②求椭圆上的动点到直线的距离的最大和最小值
选做题23	不等式选讲	①已知绝对值不等式的解集，求参数的值；②已知不等式恒成立，求参数的取值范围

其中代数部分的难点题目：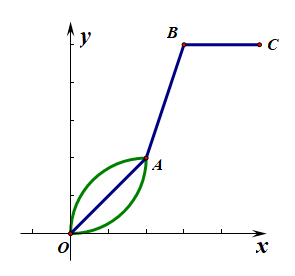

• 第4题，当杯中水的高度\(h\)沿着线段\(OA\)增长时，由于线段\(OA\)的斜率是固定不变的，故容器必然会是上下大小一致的，

当杯中水的高度\(h\)沿着上凸形曲线\(OA\)增长时，由于上凸形曲段\(OA\)的斜率是由大到小变化的，故容器必然会是上大下小形的，

当杯中水的高度\(h\)沿着下凹形曲线\(OA\)增长时，由于下凹形曲线\(OA\)的斜率是由小到大变化的，故容器必然会是下大上小形的，

• 第7题，法1：不等式性质法；法2：赋值法。

• 第8题，注意准确理解映射的概念。

• 第14题，考查由函数的奇偶性和对称性推导函数的周期性；由奇偶性\(f(x)=-f(-x)\)和对称性\(f(x)=-f(2-x)\)可以得到\(-f(-x)=-f(2-x)\)，

即\(f(x)=f(2+x)\)，故\(T=2\)。

• 第16题，由于\(f(x)=f(x-2)+1\)，可以看成是周期长的左右平移变化和上下平移变换共同作用的结果。

故\(f(2018)=f(2016)+1=f(2014)+2=f(2012)+3=\cdots=f(0)+1009\)，

由于自变量从\(2018\)到\(0\)共经过了\(\cfrac{2018}{2}=1009\)次周期长的平移变化，故最后一个式子为\(f(0)+1009\)，即\(-1+1009=1008\)；

迭代另解： \(f(2018)=f(2018-2)+1=f(2018-2\times2)+2(1+1)=f(2018-3\times2)+3(1+1+1)=f(2018-4\times2)+4(1+1+1+1)=\cdots=f(2018-1009\times2)+1009(1+1+1+\cdots+1)=f(0)+1009\)，

凤翔中学2017-2018学年度高三文科数学高考冲刺模拟试题06【粘贴版】细目表

题号	分级考点	题型和方法
选择题01	集合-集合的运算与表示	集合的运算及指数函数的性质
选择题02	复数-复数的运算及共轭复数	复数的运算
选择题03	统计-抽样方法	用数学文化背景考查随机抽样的方法
选择题04	三角函数-三角函数求值	三角函数求值中的给值求值
选择题05	解析几何-双曲线与圆	求双曲线的渐近线方程
选择题06	函数-抽象函数不等式	函数性质综合运用解抽象函数不等式
选择题07	程序框图-程序框图和三角函数最小值	程序框图下的三角函数结果的最小值计算
选择题08	立体几何-三视图	三视图还原，求其体积
选择题09	解析几何-曲线的轨迹方程	求曲线的轨迹方程
选择题10	不等式-线性规划	线性约束条件下已知最值，求参数取值范围
选择题11	三角函数-解三角形	正余弦定理应用于解三角形
选择题12	函数-不等式恒成立问题	已知不等式恒成立，求参数分取值范围
填空题13	向量-向量的关系	已知向量的垂直，求参数的值
填空题14	推理于证明-逻辑推理	简单的逻辑推理
填空题15	函数-函数性质综合运用	综合运用函数性质解不等式
填空题16	立体几何-四棱锥	求解四棱锥中的最长棱
解答题17	数列-数列的证明和求和	①用倒数法证明等差数列；②裂项相消法求和并证明
解答题18	立体几何-几何体的位置关系和计算	①求证面面垂直；②已知线面平行，求四棱锥的体积
解答题19	概率与统计-统计案例	①求概率；②完善频率分布直方图；③2X2列联表判断独立性
解答题20	解析几何- 轨迹方程	①求动点的轨迹方程；②探究直线过定点问题
解答题21	函数与导数-导数的意义及应用	①讨论含参函数的单调性；②已知函数有两个零点，求参数的取值范围；
选做题22	选修-坐标系与参数方程	①参数方程和直角坐标方程化为极坐标方程；②求弦长比值的取值范围
选做题23	选修-不等式选讲	①已知绝对值不等式恒成立，求参数的取值范围；②已知绝对值不等式解集，求参数的取值范围

其中代数部分的难点题目：

• 第4题，三角函数给值求值题，所求的式子可以转化为分式形式的二次齐次式。

• 第6题，第14题，利用函数性质可以做出函数的大致示意图，然后利用图像求解不等式；

• 第7题，程序框图和三角函数结合的题目。

第一次循环，\(k=1\)，\(S=sin\cfrac{x\pi}{2}+1\)，\(x+1\rightarrow x\)，\(1>4\)，否，

第二次循环，\(k=2\)，\(S=sin\cfrac{x\pi}{2}+1+sin\cfrac{(x+1)\pi}{2}+1=sin\cfrac{x\pi}{2}+sin\cfrac{(x+1)\pi}{2}+2\)，\(x+2\rightarrow x\)，\(2>4\)，否，

第三次循环，\(k=3\)，\(S=sin\cfrac{x\pi}{2}+sin\cfrac{(x+1)\pi}{2}+sin\cfrac{(x+2)\pi}{2}+3\)，\(x+3\rightarrow x\)，\(3>4\)，否，

第四次循环，\(k=4\)，\(S=sin\cfrac{x\pi}{2}+sin\cfrac{(x+1)\pi}{2}+sin\cfrac{(x+2)\pi}{2}+sin\cfrac{(x+3)\pi}{2}+4\)，\(x+4\rightarrow x\)，\(4>4\)，否，

第五次循环，\(k=5\)，\(S=sin\cfrac{x\pi}{2}+sin\cfrac{(x+1)\pi}{2}+sin\cfrac{(x+2)\pi}{2}+sin\cfrac{(x+3)\pi}{2}+sin\cfrac{(x+4)\pi}{2}+5\)，\(x+5\rightarrow x\)，\(5>4\)，是，

输出\(S=sin\cfrac{x\pi}{2}+sin\cfrac{(x+1)\pi}{2}+sin\cfrac{(x+2)\pi}{2}+sin\cfrac{(x+3)\pi}{2}+sin\cfrac{(x+4)\pi}{2}+5\)，

由于\(sin\cfrac{(x+1)\pi}{2}+sin\cfrac{(x+2)\pi}{2}+sin\cfrac{(x+3)\pi}{2}+sin\cfrac{(x+4)\pi}{2}=0\)，

化简为\(sin\cfrac{x\pi}{2}+5=4\)，即\(sin\cfrac{x\pi}{2}=-1\)，

故\(\cfrac{x\pi}{2}=2k\pi+\cfrac{3\pi}{2}(k\in Z)\)，即\(x=4k+3(k\in Z)\)，

则\(k=0\)时，\(x_{min}=3\)；

• 第10题，由\(y=-mx+z\)，对目标直线的斜率分类讨论即可得到答案，分类如下\(-m=0\)或\(-m>0\)或\(-m<0\)；

• 第11题，自行脑补图形，注意三角形外角定理的应用：\(\angle BDC=\angle BAD+\cfrac{\pi}{2}\)，以及方程思想。

设\(AD=x\)，在\(\Delta BCD\)中，\(\cfrac{1}{sin30^{\circ}}=\cfrac{BC}{sin\angle BDC}\)，而在\(Rt\Delta ABD\)中，\(cos\angle BAD=\cfrac{1}{x}\)

故\(BC=\cfrac{2}{x}\)，这样在\(\Delta ABC\)中，由余弦定理可得，\((x+1)^2=1^2+(\cfrac{2}{x})^2-2\cdot 1\cdot \cfrac{2}{x}\cdot cos120^{\circ}\)

从而解得\(x=\sqrt[3]{2}\)。

凤翔中学2017-2018学年度高三文科数学高考冲刺模拟试题07细目表

题号	分级考点	题型和方法
选择题01	集合-集合的运算与表示	集合的运算及对数函数的性质
选择题02	复数-复数的表示与运算	复数的运算，复数的虚部
选择题03	算法与框图-程序框图	程序框图的输出结果
选择题04	解析几何-双曲线	已知双曲线的离心率，求双曲线方程中的参数
选择题05	概率-几何概型	求面积型几何概型
选择题06	立体几何-三视图	三视图还原，求其体积
选择题07	三角函数-三角函数图像变换和性质	求变换后的三角函数的对称轴方程
选择题08	函数-函数图像的识别	由函数的性质判断、识别函数的图像
选择题09	不等式-均值不等式	由数列给定限定条件，求分式型表达式的最小值
选择题10	解析几何-抛物线与直线、圆	求线段和的最小值
选择题11	函数-函数与方程	求分段函数的零点个数
选择题12	函数-函数与导数	已知函数在给定区间有极大值，求参数的取值范围
填空题13	向量-向量的关系	已知向量的模，求向量的夹角
填空题14	数列-等差数列	等差数列的求和
填空题15	立体几何-三棱柱	数学文化背景下的三棱柱外接球体积的最小值
填空题16	函数-导数的应用+平行线法	求曲线上动点与直线上动点的距离的最小值
解答题17	三角函数-三角函数变换和解三角形	①三角变换和求周期；②求三角形的面积
解答题18	概率与统计-统计案例	①完善频率分布直方图；②求概率；③线性回归方程的应用估计
解答题19	立体几何-几何体的位置关系和计算	①求证线面平行；②求点到平面的距离
解答题20	解析几何- 椭圆	①求动点的轨迹方程；②求直线的斜率的取值范围
解答题21	函数与导数-导数的意义及应用	①讨论含参函数的单调性；②导数与不等式证明；
选做题22	选修-坐标系与参数方程	①参数方程和极坐标方程化为直角坐标方程；②利用直线的参数方程的几何意义求参数的值
选做题23	选修-不等式选讲	①解绝对值不等式；②已知含绝对值的函数有三个实数根，求参数的取值范围

其中代数部分的难点题目：

• 第8题，函数图像的辨析，先判断出偶函数，然后当\(x>0\)时，简化解析式为\(y=x\cdot lnx\)，这样其图像就能利用导数做出来，故选D。其实像\(y=x\cdot lnx\)和\(y=\cfrac{lnx}{x}\)等高频函数的图像，我们平时就需要记住她。

• 第9题，先由等差数列的性质得到\(a+b=18\)，这样由均值不等式得到\(\cfrac{1}{a}+\cfrac{25}{b}=\cfrac{1}{18}(\cfrac{1}{a}+\cfrac{25}{b})(a+b)=\cdots \ge 2\)，

当且仅当\(a=3\)，\(b=15\)时取到等号，至此问题转化为，一个数列\(1，3，\cdots，15，17\) ，问\(3，\cdots，15\) ，共有几项？

其中一个算法就是\(n=\cfrac{a_n-a_1}{d}+1=\cfrac{15-3}{2}+1=7\)。

• 第12题，已知函数在给定区间有极大值，求参数的取值范围；则其导函数方程在给定区间内必然有解，且导函数的零点必须是左正右负的变号零点。

• 第16题，曲线上的动点到直线的动点的最小值。用平行线法和导数法求得切点，所求距离的最小值转化为点线距。

• 第21题，(1)求含参函数的单调性，利用函数的图像求解；(2)利用斜率公式，先将需要证明的命题转化为只含有\(x_1，x_2\)两个变量的命题，然后变量集中，转化为只有一个变量\(t\)，最后利用作差法构造新函数证明不等式即可。

• 第22题，(2)容易忽视\(\Delta >0\)的隐含条件而出错。

凤翔中学2017-2018学年度高三文科数学高考冲刺模拟试题08细目表

题号	分级考点	题型和方法
选择题01	集合-集合的运算与表示	集合的交集并集运算及解二次不等式
选择题02	复数-复数的表示与运算	复数的相等和运算，复数的模
选择题03	立体几何-三视图	三视图还原，求其表面积
选择题04	算法与框图-程序框图	程序框图和数列求和的融合
选择题05	数列-等差数列的求和	数列的要素求解或等差数列的性质
选择题06	不等式-线性规划	求斜率型的目标函数的取值范围
选择题07	函数-函数性质	给定含参函数，判断其各种性质
选择题08	解析几何-圆与直线	圆上的动点到直线的距离的最值
选择题09	函数-分段函数不等式	求解分段函数不等式的解集
选择题10	三角函数-三角函数解析式	由图像确定正弦型解析式，并求单调区间
选择题11	解析几何-抛物线	利用已知条件求抛物线方程的$p$值
选择题12	函数-函数与导数	已知函数在给定区间恒成立，求参数的最大值
填空题13	数列-求数列的某一项的值	利用累加法和裂项法求数列中的某一项的值
填空题14	概率-古典概型	古典概型和对立事件的应用
填空题15	向量-向量的内积	向量的坐标运算和向量内积的最小值
填空题16	解析几何-三棱锥	求三棱锥外接球的表面积
解答题17	三角函数-三角函数变换和解三角形	①给值求角和两角和的余弦公式；②求三角形的面积
解答题18	立体几何-几何体的位置关系和计算	①求证面面垂直；②求几何体中两部分的体积比
解答题19	概率与统计-概率计算	①由频率分布直方图求概率；②用古典概型求概率；
解答题20	解析几何- 椭圆	①求椭圆的标准方程；②探究性问题
解答题21	函数与导数-导数的意义及应用	①利用导数的大小比较；②已知函数有两个极值点求参数的取值范围；
选做题22	选修-坐标系与参数方程	①求参数方程和直角坐标方程；②利用直线的参数方程的几何意义求值
选做题23	选修-不等式选讲	①解绝对值不等式；②求有函数图像参与的封闭图形的面积

其中代数部分的难点题目：

• 第7题， 实质是考查对函数性质的理解。\(f(x)=x^2+\cfrac{a}{x}\)，定义域是\(x\neq 0\)，

A选项，存在\(a\in R\)，使得函数\(f(x)\)为奇函数；若此选项正确，存在实数\(a\)，则对任意\(x\neq 0\)，\(f(-x)=-f(x)\)要恒成立，即\(x^2-\cfrac{a}{x}=-x^2-\cfrac{a}{x}\)要恒成立，即\(-x^2=x^2\)，不是对任意\(x\neq 0\)都恒成立的，故A选项错误；

B选项，任意\(a\in R\)，使得函数\(f(x)\)为偶函数；若此选项正确，任意实数\(a\)，则对任意\(x\neq 0\)，\(f(-x)=f(x)\)要恒成立，即\(x^2-\cfrac{a}{x}=x^2+\cfrac{a}{x}\)要恒成立，即\(\cfrac{2a}{x}=0\)，不是对任意\(x\neq 0\)都恒成立的，故B选项错误；

C选项，任意\(a>0\)，使得函数\(f(x)\)在\((-\infty，0)\)上为减函数；若此选项正确，对任意实数\(a>0\)，则对任意\(x< 0\)，\(f'(x)=2x-\cfrac{a}{x^2}<0\)恒成立，即函数\(f(x)\)在\((-\infty，0)\)上为减函数，故C选项正确；

D选项，存在\(a>0\)，使得函数\(f(x)\)在\((0，+\infty)\)上为减函数；若此选项正确，存在实数\(a>0\)，则对任意\(x>0\)，必须\(f'(x)=2x-\cfrac{a}{x^2}=\cfrac{2x^3-a}{x^2}<0\)要恒成立，但是并不能保证\(f'(x)<0\)恒成立，即函数\(f(x)\)在\((-\infty，0)\)上为减函数是错误的，故D选项错误；

综上，选C。

• 第10题中，需要注意\(A=-4\)，同时在计算单调递减区间时，应该将\(\cfrac{\pi x}{8}+\cfrac{\pi}{4}\)，代入模板函数的单调递增区间\([2k\pi-\cfrac{\pi}{2}，2k\pi+\cfrac{\pi}{2}]\)，而不是代入其单调递减区间，也是因为\(A=-4\)的原因。

• 第13题，同时用到裂项相消法和累加法。

• 第17题(1)，角化边，得到\(A\)，从而得到\(cos(A+\cfrac{\pi}{4})\)；第(2)问，需要自行做出图形，设\(CD=x\)，则\(BD=2x\)，由于是等腰三角形，则可知\(BC=AC=3x\)，在\(\Delta ACD\)中，\(AC=3x\)，\(\angle ACD=120^{\circ}\)，\(CD=x\)，\(AD=\sqrt{13}\)，由余弦定理可得\(x=1=CD\)，即\(AC=BC=3\)，故\(S_{\Delta ABC}=\cfrac{1}{2}\cdot AC\cdot BC\cdot sinC=\cfrac{9\sqrt{3}}{4}\)。

• 第19题(1)，提醒学生注意利用频率分布直方图也能计算概率，此时将每个小矩形的频率就粗略的当成概率来用，不一定每个概率都需要用古典概型来计算。

• 第21题(1)，需要求两次导数，令\(f'(x)=h(x)\)，然后再求\(h'(x)\)，其目的是为了好求\(f'(x)\)的正负，所以才引入\(h'(x)\)；由\(h'(x)>0\)知道了\(h(x)\)单调递增，故\(h(x)>h(0)=2\)，从而得到\(f'(x)>0\)，进而知道\(f(x)\)在区间\((0，+\infty)\)上单调递增，故有\(f(x)>f(0)=2\)；(2)函数\(f(x)\)有两个极值点，则\(f'(x)=0\)有两个不同的实数根，分离参数得到\(k=\cfrac{2x}{e^x}\)；从而函数\(y=k\)和函数\(y=\cfrac{2x}{e^x}\)的图像有两个交点，用导数研究函数\(y=\cfrac{2x}{e^x}\)，得到其图像，数形结合得到\(k\in(0，\cfrac{2}{e})\)。

• 第22题(2)，注意点\(A、B\)在定点\(M\)的两侧，故有\(|MA|+|MB|=|AB|=|t_1-t_2|\)；而不是\(|MA|+|MB|=|t_1|+|t_2|\)；

凤翔中学2017-2018学年度高三文科数学高考冲刺模拟试题09细目表

题号	分级考点	题型和方法
选择题01	集合-集合的运算与表示	无限集与有限集的并集，及解二次不等式
选择题02	复数-复数的表示与运算	复数的相等，纯虚数的概念
选择题03	概率-几何概型	求面积型几何概型
选择题04	统计-回归直线	给定条件下的回归直线方程的辨析
选择题05	立体几何-三视图	三视图还原，求几何体两部分体积之比
选择题06	函数-函数与方程	已知方程的根的取值范围，求参数的取值范围
选择题07	函数-函数的图像	考查学生的读图能力，利用图像解答实际问题
选择题08	向量-向量的内积	依托于三角形内的向量的内积的值
选择题09	不等式-线性规划问题	三角形的可行域中的点线距离比较
选择题10	统计案例-数学应用意识	进制的转换，将七进制转换为十进制
选择题11	立体几何-三棱锥	求三棱锥的外接球的表面积
选择题12	函数-函数与导数	已知方程在区间的根的个数，求参数的取值范围
填空题13	三角函数-三角函数的化简	三角函数的化简，给角求值
填空题14	解析几何-双曲线	求双曲线的焦距
填空题15	数列-数列的求和公式	与函数的切线相结合的数列问题，求数列的前$n$项和公式
填空题16	解析几何-椭圆与抛物线	求线段长之和的最小值
解答题17	数列-数列的通项公式和求和公式	①用$a_n$与$S_n$关系求数列的通项公式；②用裂项法求数列的和
解答题18	概率与统计-统计案例下的概率问题	①求值完善统计内容；②分层抽样；③古典概型求概率
解答题19	立体几何-四棱台	①求证线线垂直；②求点面距；
解答题20	解析几何- 椭圆	①求椭圆的标准方程；②求椭圆与直线位置中的直线的$y$截距的取值范围
解答题21	函数与导数-导数的意义及应用	①利用导数求函数的解析式；②已知函数不等式恒成立，求参数的取值范围；
选做题22	选修-坐标系与参数方程	①求线段的长度；②线段的平方和的取值范围
选做题23	选修-不等式选讲	①解绝对值不等式；②绝对值不等式的证明

其中代数部分的难点题目：

• 第6题，法1见参考答案；法2分离参数转化为\(a=\cfrac{1}{x_0}-lnx_0\)，\(x_0\in (0，1)\)，

令\(g(x)=\cfrac{1}{x}-lnx，x\in(0，1)\)，用导数做出其函数图像，其值域在\((1，+\infty)\)，故\(a\in (1，+\infty)\)；

• 第10题，不同进制的转化；把七进制数\(1325_{(7)}\)转化为十进制数为________.

分析：\(1325_{(7)}=1\times7^3+3\times7^2+2\times7^1+5\times7^0=509_{(10)}\)；

• 第12题，函数\(f(x)=\begin{cases}x^2+4x，x\leq 0\\xlnx，x>0\end{cases}\)，\(g(x)=kx-1\)，若方程\(f(x)-g(x)=0\)在\(x\in(-2，2)\)有三个实根，则实数\(k\)的取值范围是【】

A.\((1，ln2\sqrt{e})\;\;\;\;\;\) B.\((ln2\sqrt{e}，\cfrac{3}{2})\;\;\;\;\;\) C.\((\cfrac{3}{2}，2)\;\;\;\;\;\) D.\((1，ln2\sqrt{e})\cup(\cfrac{3}{2}，2)\;\;\;\;\;\)

分析：显然\(x=0\)不是方程\(f(x)-g(x)=0\)的根，故可变形为\(k=\cfrac{f(x)+1}{x}\)，

设\(\phi(x)=\cfrac{f(x)+1}{x}=\begin{cases}x+\cfrac{1}{x}+4，x<0\\\cfrac{1}{x}+lnx，x>0\end{cases}\)，即\(k=\phi(x)\)在\(x\in(-2，2)\)有三个实根，

用导数方法研究函数\(\phi(x)\)的单调性，做出其图像；

由图像可得，要使得函数\(y=k\)与函数\(y=\phi(x)\)有三个交点，则\(k\in (1，ln2\sqrt{e})\cup(\cfrac{3}{2}，2)\)

• 第15题，对正整数\(n\)，设曲线\(y=x^n(1-x)\)在\(x=2\)处的切线与\(y\)轴交点的纵坐标为\(a_n\)，则数列\(\{\cfrac{a_n}{x+1}\}\)的前\(n\)项和的公式是________.

分析：\(y=f(x)=x^n(1-x)=x^n-x^{n+1}\)，则\(f'(x)=nx^{n-1}-(n+1)x^n\)，

则\(k=f'(2)=n2^{n-1}-(n+1)2^n=n2^{n-1}-(n+1)2^{n-1}\cdot 2=n2^{n-1}-(2n+2)2^{n-1}=2^{n-1}(n-2n-2)=-(n+2)\cdot 2^n\)

又切点为\((2，-2^n)\)，则切线方程为\(y-(-2^n)=-(n+2)2^n(x-2)\)，

令\(x=0\)，得到切线与\(y\)轴交点的纵坐标\(y=(n+1)2^n=a_n\)，

令\(b_n=\cfrac{a_n}{n+1}=2^n\)，数列\(\cfrac{a_n}{n+1}\)的前\(n\)项和为\(T=2+2^2+2^3+\cdots+2^n=\cfrac{2(2^n-1)}{2-1}=2^{n+1}-2\)；

• 第21题，

已知函数\(f(x)=x^2-ax\)，\(g(x)=mx+nlnx\)，函数\(f(x)\)的图像在点\((1，f(1))\)处的切线的斜率为\(1\)，函数\(g(x)\)在\(x=2\)处取到极小值\(2-2ln2\)；

(1)求函数\(f(x)\)与\(g(x)\)的解析式；

分析：由题可知\(f'(x)=2x-a\)，又\(f'(1)=2-a=1\)，解得\(a=1\)，即\(f(x)=x^2-x\)；

又\(g'(x)=m+\cfrac{n}{x}\)，由\(g'(2)=m+\cfrac{n}{2}=0\)及\(g(2)=2m+nln2=2-2ln2\)，解得\(m=1，n=-2\)，即\(g(x)=x-2lnx\)；

(2)已知函数\(f(x)+g(x)\ge x^2-\lambda(x-1)\)对任意的\(x\in(0，1]\)恒成立，求实数\(\lambda\)的取值范围。

分析：由于\(f(x)+g(x)=x^2-2lnx\)，则\(x^2-2lnx\ge x^2-\lambda(x-1)\)对任意的\(x\in(0，1]\)恒成立，可以有以下的思路：

法1：先令\(h(x)=\lambda(x-1)-2lnx\)，则问题转化为\(h(x)\ge 0\)对任意的\(x\in(0，1]\)恒成立，

\(h'(x)=\lambda-\cfrac{2}{x}=\cfrac{\lambda x-2}{x}\)

当\(\lambda\leq 0\)时，\(h'(x)<0\)，\(h(x)\)在区间\((0，1]\)上单调递减，

\(h(x)_{min}=h(1)=0\)，即\(h(x)\ge 0\)恒成立；

当\(0<\lambda \leq 2\)时，\(h'(x)<0\)，\(h(x)\)在区间\((0，1]\)上单调递减，

\(h(x)_{min}=h(1)=0\)，即\(h(x)\ge 0\)恒成立；

当\(\lambda>2\)时，\(h'(x)<0\)在\((0，\cfrac{2}{\lambda})\)上恒成立，\(h'(x)>0\)在\((\cfrac{2}{\lambda}，1)\)上恒成立，

即\(h(x)\)在\((0，\cfrac{2}{\lambda})\)单调递减，在\((\cfrac{2}{\lambda}，1)\)上单调递增，

所以\(h(\cfrac{2}{\lambda})<h(1)=0\)，故不满足题意，注意\(h(1)=0\)，即函数\(h(x)\)恒过点\((1，0)\)

综上所述，实数\(\lambda\)的取值范围为\((-\infty，2]\)。

法2：先转化为\(\lambda(x-1)\ge 2lnx\)对任意的\(x\in(0，1]\)恒成立，

当\(x=1\)时，\(\lambda\cdot 0\ge 2ln1=0\)，\(\lambda\in R\)；

当\(x\in (0，1)\)时，分离参数得到\(\lambda \leq \cfrac{2lnx}{x-1}\)；令\(h(x)= \cfrac{2lnx}{x-1}\)，

\(h'(x)=\cfrac{\cfrac{2}{x}(x-1)-2lnx}{(x-1)^2}=\cfrac{2(1-\cfrac{1}{x}-lnx)}{(x-1)^2}\)；

令\(m(x)=1-\cfrac{1}{x}-lnx\)，则\(m'(x)=\cfrac{1}{x^2}-\cfrac{1}{x}=\cfrac{1-x}{x^2}\)，

则\(m'(x)>0\)，则\(m(x)\)在\((0，1)\)上单调递增，故\(m(x)<m(1)=0\)，故\(h'(x)=\cfrac{2m(x)}{(x-1)^2}<0\)，

则\(h(x)\)在\((0，1)\)上单调递减，故\(h(x)>h(1)=2\)(由洛必达法则求得)，即\(\lambda\leq 2\)

综上所述求交集得到，\(\lambda \in(-\infty，2]\)。

法3：由\(\lambda(x-1)\ge 2lnx\)对任意的\(x\in(0，1]\)恒成立，做函数\(y=\lambda(x-1)\)和函数\(y=2lnx\)的图像，示意图

设直线\(y=\lambda(x-1)\)与曲线\(y=2lnx\)相切于点\((x_0，y_0)\)，则有\(\cfrac{2}{x_0}=\lambda\)，\(y_0=2lnx_0\)，\(y_0=\lambda(x_0-1)\)，

求得切点坐标\((1，0)\)，此时\(\lambda=2\)，由\(\lambda\)的几何意义可知，\(\lambda\)的取值范围是\((-\infty，2]\)。

• 第22题(1)，当\(\alpha=0\)时，动直线\(l\)就变成了确定的直线\(y=2\)，做出图形，此时求\(|AB|\)的途径有三个：

其一：解析几何法，将\(y=2\)代入\((x+1)^2+(y-1)^2=2\)，解得\(x=0\)或者\(x=-2\)，故\(|AB|=|-2-0|=2\)；

其二：平面几何法，利用直线和圆中的\(Rt\Delta\)，求得弦长\(|AB|=2\)；

其三：直线的参数方程的几何意义，当\(\alpha=0\)时，直线的参数方程为\(\begin{cases}x=1+t\\y=2\end{cases}(t为参数)\)，代入\((x+1)^2+(y-1)^2=2\)，

得到\(t^2+4t+3=0\)，则\(\Delta =4>0\)，\(t_1+t_2=-4\)，\(t_1t_2=3\)，则\(|AB|=|t_1-t_2|=\sqrt{(t_1+t_2)^2-4t_1t_2}=\sqrt{4^2-4\times 3}=2\)；

• 第22题(2)，代入得到\(t^2+(4cos\alpha+2sin\alpha)t+3=0\)，由\(\Delta=(2sin\alpha+4cos\alpha)^2-4\times3>0\)得到\([2\sqrt{5}sin(\alpha+\phi)]^2-12>0\)，即\(\cfrac{3}{5}<sin^2(\alpha+\phi)\leq 1\)；

由韦达定理得到\(t_1+t_2=-(4cos\alpha+2sin\alpha)\)，\(t_1t_2=3\)，

则\(|PA|^2+|PB|^2=t_1^2+t_2^2=(t_1+t_2)^2-2t_1t_2=(4cos\alpha+2sin\alpha)^2-6=20sin^2(\alpha+\phi)-6\)，

则\(|PA|^2+|PB|^2\in (6，14]\)；

凤翔中学2017-2018学年度高三文科数学高考冲刺模拟试题10细目表

题号	分级考点	题型和方法
选择题01	集合-集合的运算与表示	无限集与有限集的并集，及解对数二次不等式
选择题02	复数-复数的几何意义	复数的几何意义，解不等式组
选择题03	向量-向量的位置关系	由向量的共线和垂直求参数值
选择题04	函数-函数的零点	利用函数的零点进行大小比较
选择题05	解析几何-双曲线	求双曲线的渐近线
选择题06	概率-互斥事件的概率	求互斥事件的概率
选择题07	立体几何-三视图	三视图还原，求几何体的表面积
选择题08	函数-分段函数与方程	求解分段函数方程
选择题09	常用逻辑-充要条件	命题的化简和充要条件的判断
选择题10	数列-数列求和	用一次函数表达的数列的求和问题
选择题11	立体几何-四面体	求四面体的外接球的表面积
选择题12	函数-函数与方程	已知二元方程相等，求其自变量的差值的最小值
填空题13	函数-恒成立问题	用真命题的形式给出的恒成立求参数值
填空题14	推理与证明-逻辑推理	逻辑推理的运用
填空题15	函数-函数与方程	可转化为方程仅有一个根问题，求参数的取值范围
填空题16	解析几何-直线与抛物线	求三角形的面积
解答题17	三角函数-向量与解三角形	①向量背景下的三角函数化简求$sinA$；②求三角形面积的最大值
解答题18	立体几何-半圆柱和四棱锥组合	①求证线面垂直；②求几何体体积；
解答题19	概率与统计-统计案例下的概率问题	①求古典概型的概率；②平均数和方差的计算和应用
解答题20	解析几何- 椭圆	①求椭圆的标准方程；②求直线的斜率的取值范围
解答题21	函数与导数-导数的意义及应用	①讨论含参函数的单调性；②已知直线和曲线交点的横坐标，求区间端点参数的取值范围；
选做题22	选修-坐标系与参数方程	①参数方程化为普通方程；②转化为三角函数求点线距的最小值
选做题23	选修-不等式选讲	①解绝对值不等式；②已知绝对值不等式解集非空，求参数取值范围

其中代数部分的难点题目：

• 第8题，已知\(f(x)=\begin{cases}1，&x\in[0，1]\\x-3，&x\notin[0，1]\end{cases}\)，则使得\(f(f(x))=1\)成立的\(x\)的取值范围是【】

A.\([0，1]\hspace{2cm}\) B.\([0，1]\cup\{7\}\hspace{2cm}\) C.\([0，1]\cup [3，4]\hspace{2cm}\) D.\([0，1]\cup[3，4]\cup\{7\}\)

法1：直接求解法，本题目属于求解分段函数方程，可以将\(f(x)\)这个整体视为已知中的\(x\)，则原分段函数方程等价于

第一种情形，\(0\leq f(x)\leq 1\)且\(f(x)=1\)；或第二种情形，\(f(x)-3=1\)且\(f(x)\notin[0，1]\)，

其中第一种可化简为\(0\leq f(x)\leq 1\)，再等价转化为\(\begin{cases}x\in[0，1]\\0\leq f(x)=1\leq 1\end{cases}\)或\(\begin{cases}x\notin[0，1]\\0\leq x-3\leq 1\end{cases}\)

解得\(0\leq x\leq 1\)或\(3\leq x\leq 4\)；

第二种可化简为\(f(x)=4\)，再等价转化为\(\begin{cases}x\in[0，1]\\f(x)=1=4\end{cases}\)或\(\begin{cases}x\notin[0，1]\\x-3=4\end{cases}\)，解得\(x=7\)；

综上所述，\(x\)的取值范围是\([0，1]\cup[3，4]\cup\{7\}\)，故选D。

法2：验证法，由题目可知，

当\(x=7\)时，\(f(f(x))=f(f(7))=f(4)=f(1)=1\)，故\(x=7\)在解集内；

当\(x=4\)时，\(f(f(x))=f(f(4))=f(1)=1\)，故\(x=4\)在解集内；

当\(x=1\)时，\(f(f(x))=f(f(1))=f(1)=1\)，故\(x=1\)在解集内；故选D。

• 第9题，\(|x-1|+|x-3|\ge |(x-1)-(x-3)|=2\)，故\([|x-1|+|x-3|]_{min}=2\)；

• 第12题，已知函数\(f(x)=ln\cfrac{x}{2}+\cfrac{1}{2}\)，\(g(x)=e^{x-2}\)，若\(g(m)=f(n)\)成立， 则\(n-m\)的最小值为【】

A.\(1-ln2\hspace{2cm}\) B.\(ln2\hspace{2cm}\) C.\(2\sqrt{e}-3\hspace{2cm}\) D.\(e^2-3\)

分析：不妨设\(g(m)=f(n)=t\)，则\(e^{m-2}=ln\cfrac{n}{2}+\cfrac{1}{2}=t(t>0)\)，

(编者注：此处引入第三方变量\(t\)，可以将\(m、n\)用含有\(t\)的表达式来刻画，则二元函数就此转化为了一元函数，我们就可以用导数求其最值了)

则\(m-2=lnt\)，\(m=2+lnt\)；\(ln\cfrac{n}{2}=t-\cfrac{1}{2}\)，则\(n=2e^{t-\frac{1}{2}}\)；

故\(n-m=2e^{t-\frac{1}{2}}-2-lnt(t>0)\) ，

令\(h(t)=2e^{t-\frac{1}{2}}-2-lnt(t>0)\)，\(h'(t)=2e^{t-\frac{1}{2}}-\cfrac{1}{t}\)，(增+增=增)

易知\(h'(t)\)在\((0，+\infty)\)上单调递增，且\(h(\cfrac{1}{2})=0\)；

当\(t>\cfrac{1}{2}\)时，\(h'(t)>0\)，当\(0<t<\cfrac{1}{2}\)时，\(h'(t)<0\)，

即当\(t=\cfrac{1}{2}\)时，\(h(t)\)取得极小值也是最小值，\(h(t)_{min}=h(\cfrac{1}{2})=2e^{\frac{1}{2}-\frac{1}{2}}-2-ln\cfrac{1}{2}=ln2\)，故选B.

• 第15题，已知点\(P\)和点\(Q\)分别是函数\(y=e^x\)和函数\(y=kx\)图像上的点，若有且只有一组点\((P，Q)\)关于直线\(y=x\)对称，则\(k=\)________.

分析：由于\(y=e^x\)关于\(y=x\)的对称函数为\(y=lnx\)，

则由函数\(y=e^x\)和函数\(y=kx\)有且只有一组点\((P，Q)\)关于直线\(y=x\)对称，

可知，函数\(y=lnx\)和函数\(y=kx\)有且只有一个交点，

接下来有两个思路：

思路一：用函数图像可知，

当\(k\leq 0\)时，函数\(y=lnx\)和函数\(y=kx\)有且只有一个交点；

当\(k>0\)时，两个函数要有且只有一个交点，只能相切，设切点为\((x_0，y_0)\)，则有\(\cfrac{1}{x_0}=k\)，\(y_0=lnx_0\)，\(y_0=kx_0\)，

从而求得切点为\((e，1)\)，即此时的切线斜率为\(k=\cfrac{1}{e}\)；

综上可知，\(k\)的值为\(k\leq 0\)或\(k=\cfrac{1}{e}\)；示意图

思路二：即方程\(lnx=kx\)有且只有一个根，即方程\(k=\cfrac{lnx}{x}\)有且只有一个根，

即函数\(y=k\)和函数\(=\cfrac{lnx}{x}\)有且只有一个交点，

先用导数研究函数\(y==\cfrac{lnx}{x}\)的单调性，从而做出其函数图像，

由函数图像可知，\(k\)的值为\(k\leq 0\)或\(k=\cfrac{1}{e}\)；示意图

转载于:https://www.cnblogs.com/wanghai0666/p/8946053.html