二叉树先序遍历；（1）先序访问根节点  （2）先序访问左子树 （3）先序访问右子树

二叉树中序遍历；（1）中序访问根节点  （2）中序访问左子树 （3）中序访问右子树

二叉树后序遍历；（1）后序访问根节点  （2）后序访问左子树 （3）后序访问右子树

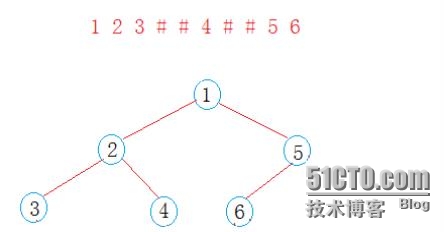
测试用例：int a[10]={'1','2','3','#','#','4','#','#','5','6'}

wKiom1czMXCx_nz5AAB0jqGXn5E099.jpg

代码：

#include<iostream>
using namespace std;
#include<queue>
#include<stack>
template<class T>
struct BinaryTreeNode
{
    BinaryTreeNode<T>* _left;
    BinaryTreeNode<T>* _right;
    T _data;
    BinaryTreeNode(const T& d)
        :_left(NULL)
        ,_right(NULL)
        ,_data(d)
    {}
};
template<class T>
class BinaryTree
{
public:
    BinaryTree()
        :_root(NULL)
    {}
    BinaryTree(const T* a,size_t size,const T& invalid)
    {
        size_t index = 0;
        _root = _Create(a,size,index,invalid);
    }
    //BinaryTree(const BinaryTree<T>& d)
    //{
    //    BinaryTreeNode<T> root = NULL;

    //}
    BinaryTree<T>& operator = (const BinaryTree<T>& d)
    {
        swap(root,d._root );
    }
    void PrevOrder()
    {
       _PrevOrder(_root);
    }
    void InOrder()
    {
       _InOrder(_root);
    }
    size_t Size()
    {
        _Size(_root);
    }
    size_t Depth()
    {
        return _Depth(_root);
    }
    size_t LeafSize()
    {
        return _LeafSize( _root);
    }
    void LevelOrder()
   {
        _LeavelOrder();
   }
    void PrevOrder_NonR()
    {
        _PrevOrder_NonR();
    }
    void InOrder_NonR()
    {
        _InOrer_NonR();
    }
    void PostOrder_NonR()
    {
        _PostOrder_NonR();
    }
public:

protected:
   BinaryTreeNode<T>* _Create(const T*a,size_t size,size_t& index,const T& invalid)
   {
       BinaryTreeNode<T> *root = NULL;
       while(index<size && a[index] != invalid)
       {
           root = new BinaryTreeNode<T> (a[index]);
           root->_left = _Create(a,size,++index,invalid);
           root->_right = _Create(a,size,++index,invalid);
       }
       return root;
   }
   void _PrevOrder(BinaryTreeNode<T>* root)
   {
       if(root == NULL)
       {
            return;
       }
       cout<<root->_data<<" " ;
       _PrevOrder(root->_left );
       _PrevOrder(root->_right);
   }
   void _InOrder(BinaryTreeNode<T>* root)
   {    
        if(root == NULL)
        {
            return;
        }
        _InOrder (root->_left );
        cout<<root->_data<<" " ;
        _InOrder (root->_right );
   }
   size_t _size(BinaryTreeNode<T>* root)
   {
        if(root == NULL)
        {
            return 0;
        }
        return _Size(root->_left )+_Size(root->_right )+1;
   }
   size_t _Depth(BinaryTreeNode<T>* root)
   {
      if(root == NULL)
      {
        return 0;
      }
      int left = _Depth(root->_left )+1;
      int right = _Depth (root->_right )+1;
      return (left>right?left:right);
   }
   size_t _LeafSize(BinaryTreeNode<T>* root)
   {
        if(root == NULL)
        {
            return 0;
        }
        if(root->_left == NULL && (root->_right == NULL))
        {
            return 1;
        }
        return _LeafSize(root->_left)+_LeafSize (root->_right);
   }

    void _LeavelOrder()
    {
        queue<BinaryTreeNode<T>*>q;
        if(_root)
        {
            q.push(_root);
        }
        while(!q.empty())
        {
            BinaryTreeNode<T>* front = q.front();
            cout<<front._data<<" ";
            if(_root->_left)
            {
                q.push(_root->_left);
            }
            if(_root->_right)
            {
                q.push(_root->_right);
            }
            q.pop();
        }
        cout<<endl;
    }
    void _PrevOrder_NonR()
    {
        stack<BinaryTreeNode<T>*>s;
        BinaryTreeNode<T>* cur = _root;
        while(cur||!s.empty())
        {
            
            while(cur )
            {
                cout<<cur->_data <<" "; 
                s.push(cur);
                cur = cur->_left ;
            }
            if(!s.empty())
            {
                BinaryTreeNode<T>* top = s.top();
                cur = top->_right ;
                s.pop();
            }            
        }
    }
    void _InOrer_NonR()
    {
        stack<BinaryTreeNode<T>*> s;
        BinaryTreeNode<T>* cur = _root;
        while(cur||!s.empty())
        {
            while(cur)
            {
               s.push(cur);
               cur = cur->_left ;
            }
            BinaryTreeNode<T>* Top = s.top();
            cout<<Top->_data<<" ";            
            cur = Top->_right ;
            s.pop();
        }
        cout<<endl;
    }

    void _PostOrder_NonR()
    {
        BinaryTreeNode<T>* cur = _root;
        stack<BinaryTreeNode<T>*>s; 
        BinaryTreeNode<T>* prev = NULL;
        while(cur||!s.empty())
        {
            while(cur)
            {
                s.push(cur);
                cur = cur->_left ;
            }
            BinaryTreeNode<T>* top = s.top();
            if(top->_right == NULL||top->_right == prev)
            {
                cout<<top->_data <<" ";
                s.pop();
                prev = top;
            }
            else
            cur = top->_right ;
            //cout<<endl;
        }
    }
protected:
    BinaryTreeNode<T>* _root;
};
int main()
{
    int a1[10] = {1,2,3,'#','#',4,'#','#',5,6};
    BinaryTree<int>  b1(a1,10,'#');
    //b1.InOrder();
    //b1.InOrder_NonR ();
    //b1.Depth();
    //b1.PrevOrder_NonR();
    b1.PostOrder_NonR();
    system("pause");
    return 0;
}