一、普里姆算法(Prim)

1、条件：图为邻接矩阵结构(Adjacency List)

2、原理：假设 WN=(V,{E}) 是一个含有 n 个顶点的连通网，TV 是 WN 上最小生成树中顶点的集合，TE 是最小生成树中边的集合。显然，在算法执行结束时，TV=V，而 TE 是 E 的一个子集。在算法开始执行时，TE 为空集，TV 中只有一个顶点，因此，按普里姆算法构造最小生成树的过程为：在所有“其一个顶点已经落在生成树上，而另一个顶点尚未落在生成树上”的边中取一条权值为最小的边，逐条加在生成树上，直至生成树中含有 n-1条边为止

3、code

void MiniSpanTree_Prim(MGraph G)
{
    int min,i,j,k;
    int adjvex[MAXVEX];    /*保存相关顶点下标*/
    int lowcost[MAXVEX];    /*保存相关顶点的权值，存放的是最小生成树到剩下顶点的最小权值*/
    int lowcost[0]=0;    /*初始化第一个权值为0,即v0加入生成树，假设v0下标为0*/
    for(i=1;i<G.numVertexes;i++)
    {
        lowcost[i]=G.arc[0][i];    /*arc为邻接矩阵的弧数组*/
                                   /*将第一个顶点v0与之有边的权值存入数组*/
        adjvex[i]=0;    /*初始化都为v0的下标*/
    }
    for(i=1;i<G.numVertexes;i++)
    {
        min=INFINITY;    /*初始化最小权限值为∞，便于比较*/
        j=1;i=0;
        while(j<G.numVertexes)
        {
            if(lowcost[j]!=0&&lowcost[j]<min)    /*lowcost[j]==0表示已将该顶点归入生成树了，不必比较了*/
            {
                min=lowcost[j];    /*当前权值为最小值*/
                k=j;     /*记录该值*/
            }
            j++;
        }
        printf("(%d,%d)",adjvex[k],k);    /*即adjvex[k]顶点与k顶点之间有同路*/
        lowcost[k]=0;    /*将当前顶点的权值设为0，表示将该顶点归入生成树*/
        for(j=1;j<G.numVertexes;j++)
        {
            /*下面的循环的意思是在所有“其一个顶点已经落在生成树上，而另一个顶点尚未落在生成树上”的边中取一条权值为最小的边*/
            if(lowcost[j]!=0 && G.arc[k][j]<lowcost[j])
            {
                /*若下标为k顶点各个权值小于此前这些顶点未被加入生成树权值*/
                lowcost[j]=G.arc[k][j];    /*将较小的权值存入lowcost*/
                adjvex[j]=k;    /*将小标为k的顶点存入adjvex*/
            }
        }
    }
}

一、克鲁斯卡尔算法(Kruskal)

1、条件：边集数组结构(Edge)

2、原理：设有一个有n个顶点的连通网N={V,E},最初先构造一个只有n个顶点，没有边的非连通图T={V, E},图中每个顶点自成一个连通分量。当在E中选到一条具有最小权值的边时,若该边的两个顶点落在不同的连通分量上，则将此边加入到T中；否则将此边舍去，重新选择一条权值最小的边。如此重复下去，直到所有顶点在同一个连通分量上为止。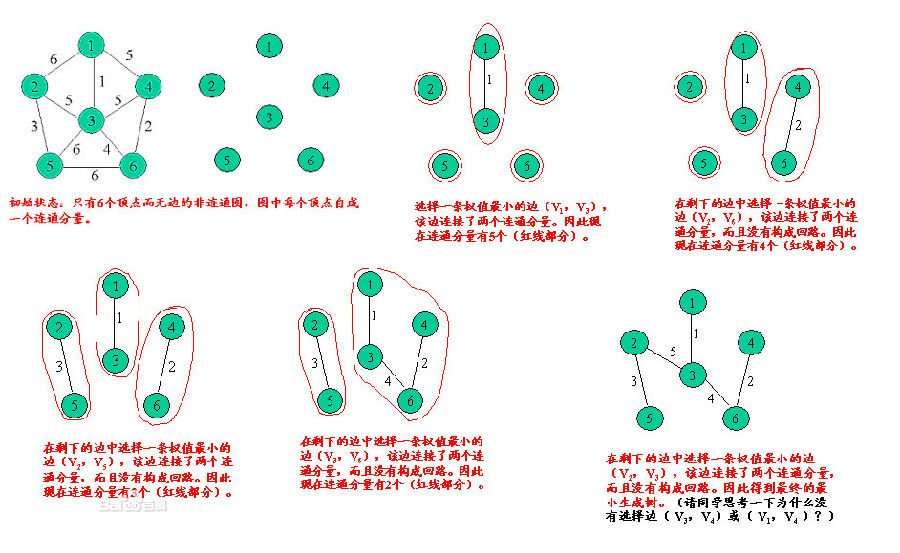170456313.png

3、code

/*对编辑数组Edge结构的定义*/
typedef struct
{
    int begin;    /*起始顶点下标*/
    int end;    /*终止顶点下标*/
    int weight;    /*权值*/
}Edge;
/*Kruskal算法生成最小生成树*/
void MiniSpanTree_Kruskal(MGraph G)
{
    int i,n,m;
    Edge edges[MAXEDGE];    /*定义边集数组*/
    int parent[MAXVEX];        /*定义一数组用来判断边与边是否行程环路*/
    /*此处省略将邻接矩阵G转化为边集数组edges并按权由小到大排序的代码*/
    for(i=0;i<G.numVertexes;i++)
    {
        parent[i]=0;    /*初始化数组值为0*/
    }
    for(i=0;i<G.numVertexes;i++)
    {
        n=Find(parent,edges[i].begin);
        m=Find(parent,edges[i].end);
        if(n!=m)    /*说明此边没有与现有的生成树行程环路*/
        {
            parent[n]=m;    /*将此边的结尾顶点放入小标为起点的parent中*/
                            /*表示n与m在同一个集合中*/
            printf("(%d,%d) %d",edges[i].begin,edges[i].end,edges[i].weight);
        }
    }
}

int Find(int *parent,int f)    /*查找连线顶点的尾部下标*/
{
    while（parent[f]>0)
        f=parent[f];
    return f;
}