本文精选了2019届宝鸡理数质检中的典型数学题目，包括解析几何、数列、积分、概率论等多个领域的难点问题，通过详细解析帮助读者深入理解解题技巧。
前言
选择题
例1-6参见图片解答；
例7【2019届宝鸡理数质检Ⅲ第7题】已知\(M\)，\(N\)是椭圆\(\cfrac{x^2}{a^2}+\cfrac{y^2}{b^2}=1\) \(a>b>0\)上关于原点对称的两个点，\(P\)是椭圆上任意一点，直线\(PM\)，\(PN\)的斜率分别是\(k_1\)、\(k_2\)，若\(|k_1k_2|=\cfrac{1}{4}\)，则椭圆的离心率为【】
分析：采用特殊化策略求解，由于点\(M\)，\(N\)是椭圆\(\cfrac{x^2}{a^2}+\cfrac{y^2}{b^2}=1\) \(a>b>0\)上关于原点对称的任意的两个点，那么就可以特殊化为椭圆的左右两个顶点，又点\(P\)是椭圆上任意一点，那么就可以特殊化为椭圆上的上顶点，
那么如何让他们满足题目的条件呢，我们可以这样想，只要调整椭圆的三个参数恰当，就可以让其满足题目的条件，这样在这种特殊条件下，
\(k_1=k_{PM}=\cfrac{y_2-y_1}{x_2-x_1}=\cfrac{b-0}{0+a}\)，\(k_2=k_{PN}=\cfrac{b-0}{0-a}\)，
则\(|k_1k_2|=|\cfrac{b^2}{-a^2}|=\cfrac{b^2}{a^2}=\cfrac{1}{4}\)，故\(a^2=4b^2\)，\(c^2=a^2-b^2=3b^2\)，
则\(e^2=\cfrac{c^2}{a^2}=\cfrac{3b^2}{4b^2}=\cfrac{3}{4}\)，故\(e=\cfrac{c}{a}=\cfrac{\sqrt{3}}{2}\)。故选\(C\)。
例8【2019届宝鸡理数质检Ⅲ第8题】一个算法的程序框图如图所示，若该程序输出\(\cfrac{25}{42}\)，则判断框中应该填入的条件是【】
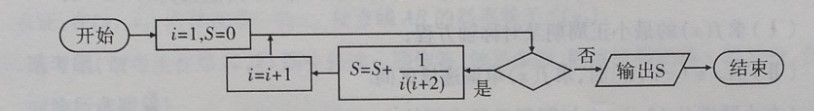
分析：按照框图的思路执行以下几个步骤，
\(R_1\)中，\(i=1，S=0\)，是，\(S=\cfrac{1}{2}(1-\cfrac{1}{3})\)，\(i=2\)；
\(R_2\)中，\(i=2，S=\cfrac{1}{2}(1-\cfrac{1}{3})\)，是，\(S=\cfrac{1}{2}(1-\cfrac{1}{3}+\cfrac{1}{2}-\cfrac{1}{4})\)，\(i=3\)；
\(R_3\)中，\(i=3，S=\cfrac{1}{2}(1-\cfrac{1}{3}+\cfrac{1}{2}-\cfrac{1}{4})\)，是，\(S=\cfrac{1}{2}(1-\cfrac{1}{3}+\cfrac{1}{2}-\cfrac{1}{4}+\cfrac{1}{3}-\cfrac{1}{5})\)，\(i=4\)；
\(R_4\)中，\(i=4，S=\cfrac{1}{2}(1+\cfrac{1}{2}-\cfrac{1}{4}-\cfrac{1}{5})\)，是，\(S=\cfrac{1}{2}(1+\cfrac{1}{2}-\cfrac{1}{4}-\cfrac{1}{5}+\cfrac{1}{4}-\cfrac{1}{6})\)，\(i=5\)；
\(R_5\)中，\(i=5，S=\cfrac{1}{2}(1+\cfrac{1}{2}-\cfrac{1}{5}-\cfrac{1}{6})\)，是，\(S=\cfrac{1}{2}(1+\cfrac{1}{2}-\cfrac{1}{5}-\cfrac{1}{6}+\cfrac{1}{5}-\cfrac{1}{7})=\cfrac{1}{2}(1+\cfrac{1}{2}-\cfrac{1}{6}-\cfrac{1}{7})=\cfrac{25}{42}\)，\(i=6\)；
\(R_6\)中，\(i=6，S=\cfrac{25}{42}\)，否，输出\(S=\cfrac{25}{42}\)，结束；即当\(i=6\)时，应该满足“否”而不是“是”，故应该填入的是\(i\leq 5\)。
例9【2019届宝鸡理数质检Ⅲ第9题】【2018江西南昌二模】在《周易》中，长横表示阳爻，两个短横表示阴爻．有放回地取阳爻和阴爻三次合成一卦，共有\(2^3＝8\)种组合方法，这便是《系辞传》所说“太极生两仪，两仪生四象，四象生八卦”．有放回地取阳爻和阴爻一次有2种不同的情况，有放回地取阳爻和阴爻两次有4种情况，有放回地取阳爻和阴爻三次，有8种情况．所谓的“算卦”，就是两个八卦的叠合，即共有放回地取阳爻和阴爻六次，得到六爻，然后对应不同的解析．在一次所谓“算卦”中得到六爻，这六爻恰好有三个阳爻、三个阴爻的概率是【】
分析：六爻共有\(2^6=64\)种，其中三阳爻三阴爻有\(C_6^3=20\)种，说明：相当于从\((阳+阴)^6\)展开式中取三阳爻三阴爻，故有\(C_6^3\cdot C_3^3=20\)种，则所求概率为\(P=\cfrac{20}{64}=\cfrac{5}{16}\)，故选\(C\)。
例10【2019届宝鸡理数质检Ⅲ第10题】定义在\(R\)上的函数\(y=f(x)\)满足以下三个条件：
①对于任意的\(x\in R\)，都有\(f(x+1)=f(x-1)\)；
②函数\(y=f(x+1)\)的图像关于\(y\)轴对称；
③对于任意的\(x_1，x_2\in [0，1]\)，都有\([f(x_1)-f(x_2)](x_1-x_2)>0\)；
则\(f(\cfrac{3}{2})\)、\(f(2)\)、\(f(3)\)的大小关系是【】
分析：本题目考查函数的各种性质的综合运用，其中主要涉及的是函数的奇偶性、周期性、对称性、单调性；
由①可知，函数的周期为\(T=2\)，故可以简化其中的两项，\(f(2)=f(0)\)，\(f(3)=f(1)\)；
由②，通过图像的平移，可知函数\(y=f(x)\)的对称轴为直线\(x=1\)，即函数满足条件\(f(x)=f(2-x)\)，再赋值得到，\(f(\cfrac{3}{2})=f(2-\cfrac{3}{2})=f(\cfrac{1}{2})\)；
由③可知函数\(f(x)\)在区间\([0，1]\)上单调递增，由于\(1>\cfrac{1}{2}>0\)，故\(f(1)>f(\cfrac{1}{2})>f(0)\)，即满足\(f(3)>f(\cfrac{3}{2})>f(2)\)，故选\(D\)。
例11【2019届宝鸡理数质检Ⅲ第11题】异面直线\(a\)，\(b\)所成的角为\(\cfrac{\pi}{6}\)，直线\(a\perp c\)，则异面直线\(b\)和\(c\)所成角的范围是【】
分析：由于求异面直线所成角的范围，故需要先明确其允许的最大范围，是\((0，\cfrac{\pi}{2}]\)，怎么理解呢？采用简单原则，当同一平面内的两条直线相交时形成两对对顶角，其中的邻角互补，这样我们刻画其位置关系时，仅仅只需要\([0，\cfrac{\pi}{2}]\)范围内的角就足够了，不需要范围为\([0，\pi]\)，那么异面直线所成角的范围就成了\((0，\cfrac{\pi}{2}]\)，
再者我们需要将已知的直线安放在空间，最好的依托就是正方体和长方体等模型，如下图所示，
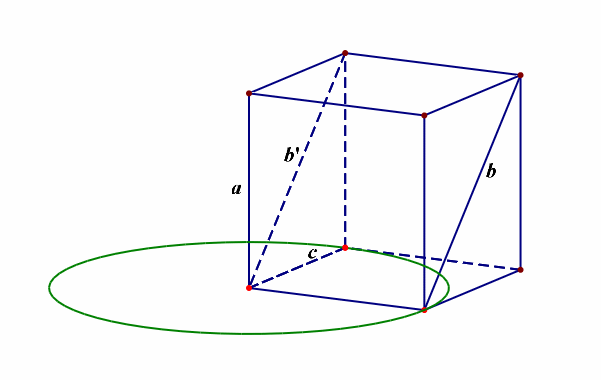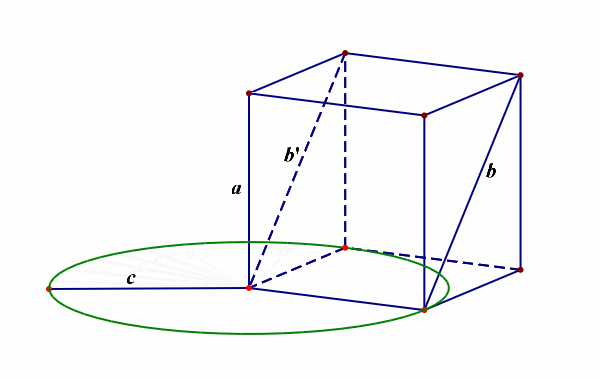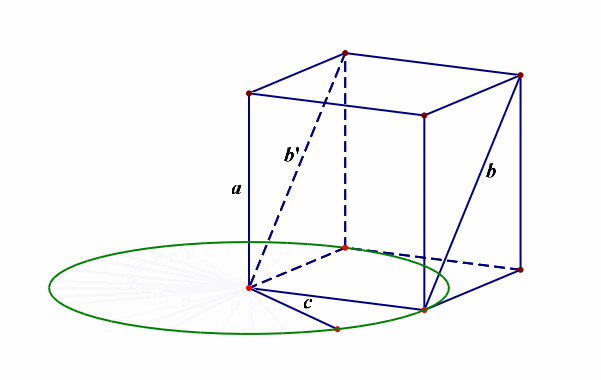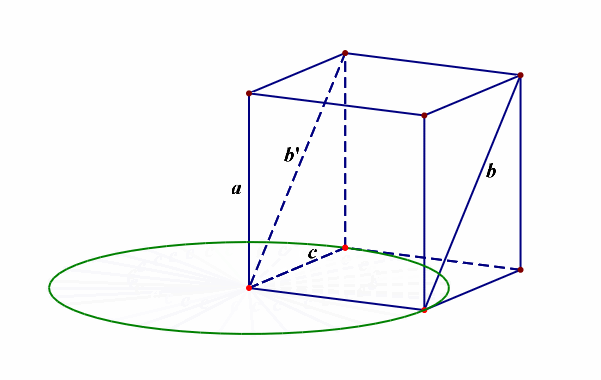
当异面直线\(a\)，\(b\)所成的角为\(\cfrac{\pi}{6}\)，直线\(a\perp c\)，那么异面直线\(b\)和\(c\)所成角的范围最小是\(\cfrac{\pi}{2}-\cfrac{\pi}{6}=\cfrac{\pi}{3}\)，最大是\(\cfrac{\pi}{2}+\cfrac{\pi}{6}=\cfrac{2\pi}{3}\)，又由于刻画异面直线所成角的范围限制，故只能是\([\cfrac{\pi}{3}，\cfrac{\pi}{2}]\)，故选\(A\)。
例12【2019届宝鸡理数质检Ⅲ第12题】双曲线\(\cfrac{x^2}{a^2}-\cfrac{y^2}{b^2}=1\) \((a>0\)，\(b>0)\)的左右焦点分别为\(F_1\)，\(F_2\)，渐近线分别为\(l_1\)，\(l_2\)，过点\(F_1\)且与\(l_1\)垂直的直线分别交\(l_1\)，\(l_2\)于点\(P\)和\(Q\)，若满足\(\overrightarrow{OF_1}+\overrightarrow{OQ}=2\overrightarrow{OP}\)，则双曲线的渐近线方程为【】
法1：解析几何法，只要求得\(a\)、\(b\)的值即可；如图所示，由条件\(\overrightarrow{OF_1}+\overrightarrow{OQ}=2\overrightarrow{OP}\)可知，点\(P\)是线段\(F_1Q\)的中点，又由于\(\angle F_1PO=\cfrac{\pi}{2}\)，故\(\triangle OF_1Q\)为等腰三角形，且\(|OF_1|=|OQ|\)，且可知渐近线方程为\(y=\pm\cfrac{b}{a}x\)，
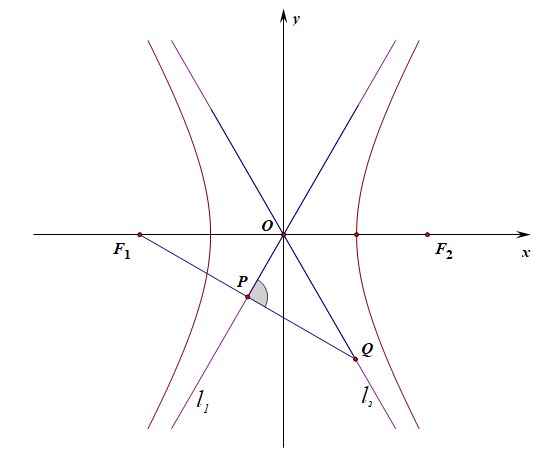
由于\(l_1:y=\cfrac{b}{a}x\)，则可知与\(l_1\)垂直的直线\(F_1Q:y=-\cfrac{a}{b}(x+c)\)①，又\(l_2:y=-\cfrac{b}{a}x\)②，两式联立，
解得交点\(Q(\cfrac{a^c}{b^2-a^2}，-\cfrac{abc}{b^2-a^2})\)，又由于\(|OF_1|=|OQ|\)，
则有\(c^2=(\cfrac{a^c}{b^2-a^2})^2+(-\cfrac{abc}{b^2-a^2})^2\)，化简整理得到，\(b^2=3a^2\)，即\(\cfrac{b}{a}=\sqrt{3}\)，故渐近线为\(y=\pm \sqrt{3}x\)，故选\(C\)。
说明：法1的计算很是麻烦和复杂。
法2：平面几何法，只要求得斜率或者倾斜角即可；如图所示，由条件\(\overrightarrow{OF_1}+\overrightarrow{OQ}=2\overrightarrow{OP}\)可知，点\(P\)是线段\(F_1Q\)的中点，又由于\(\angle F_1PO=\cfrac{\pi}{2}\)，故\(\triangle OF_1Q\)为等腰三角形，且\(|OF_1|=|OQ|\)，
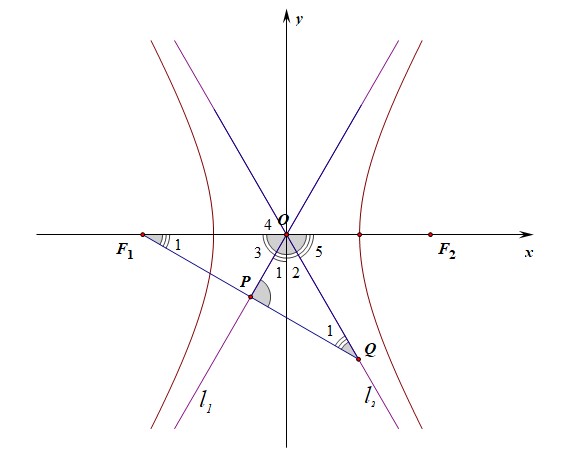
由双曲线的性质可知，\(x\)轴平分\(\angle 3\)和\(\angle 4\)，\(y\)轴平分\(\angle 1\)和\(\angle 2\)，\(\angle 4=\angle 5\)，
则\(\angle 3+\angle 1=\cfrac{\pi}{2}\)，又在等腰三角形\(\triangle OF_1Q\)中，\(\angle 3+4\angle 1=\pi\)，
从而解得\(\angle 1=\cfrac{\pi}{6}\)，\(\angle 3=\cfrac{\pi}{3}\)，
故渐近线的斜率为\(k=\pm tan(\cfrac{\pi}{3})=\pm \sqrt{3}\)，故渐近线为\(y=\pm \sqrt{3}x\)，故选\(C\)。
填空题
例13【2019届宝鸡理数质检Ⅲ第13题】若数列\(a_1+2a_2+2^2a_3+\cdots+2^{n-1}a_n=8n\) \((n\in N^*)\)，则\(a_n\)=__________。
分析：本题目的左端涉及两个数列，一个数列为\(\{a_n\}\)，设其前\(n\)项和为\(T_n\)，另一个数列为\(\{2^{n-1}a_n\}\)，设其前\(n\)项和为\(S_n\)，右端可以看出\(f(n)\)，故本题目是利用\(2^{n-1}a_n\)和\(S_n\)的关系，先求出数列\(\{2^{n-1}a_n\}\)的通项公式，然后反解出\(a_n\)即可；
由\(n\ge 1\)时，\(S_n=a_1+2a_2+2^2a_3+\cdots+2^{n-1}a_n=8n\)① ，
则\(n\ge 2\)时，\(S_{n-1}=a_1+2a_2+2^2a_3+\cdots+2^{n-2}a_{n-1}=8(n-1)\)② ，
两式做差，得到，
当\(n\ge 2\)时，\(S_n-S_{n-1}=2^{n-1}a_n=8\)，即\(a_n=8\cdot 2^{1-n}=2^{4-n}\)，
当\(n=1\)时，\(S_1=a_1=8=2^{4-1}\)，满足上式，
故\(a_n=2^{4-n}(n\in N^*)\)；
例14【2019届宝鸡理数质检Ⅲ第14题】若\(a=\displaystyle\int_{0}^{\pi} sinx\, dx\)，则\((\cfrac{1}{x}-x)^{5a}\)的展开式中\(x^2\)项的系数为___________。
分析：\(a=\displaystyle\int_{0}^{\pi} sinx\, dx=-cosx|_0^{\pi}=2\)，即求\((\cfrac{1}{x}-x)^{10}\)的展开式中\(x^2\)项的系数，用通项公式法，可知所求为\(210\)；
例15【2019届宝鸡理数质检Ⅲ第15题】一个圆锥的轴截面是一个边长为2的等边三角形，则这个圆锥的侧面积为____________。
分析：由题可知，底面圆的半径为\(r=1\)，圆锥的侧面展开图是弧长为\(2\pi r=2\pi\)，半径为2的扇形，故其侧面积为\(S_{扇形}=\cfrac{1}{2}\times 2\pi\times 2=2\pi\)。
例16【2019届宝鸡理数质检Ⅲ第16题】已知函数\(y=INT(x)\)叫做取整函数，它表示\(y\)等于不超过\(x\)的最大整数，如\(INT(0.89)=0\)，\(INT(2.90)=2\)，已知\(a_n=INT(\cfrac{1}{7}\times 2^n)\)，\(b_1=a_1\)，\(b_n=a_n-2a_{n-1}\)，\((n\in N^*，n\ge 2)\)，则\(b_{2019}\)=___________。
分析：自然会想到验证是否为周期数列，
\(b_1=INT(\cfrac{2}{7})=0\)，则\(a_1=0\)；
\(b_2=a_2-2a_1=INT(\cfrac{4}{7})-2\times 0=0-0=0\)，\(a_2=0\)；
\(b_3=a_3-2a_2=INT(\cfrac{8}{7})-2\times 0=1-0=1\)，\(a_3=1\)；
\(b_4=a_4-2a_3=INT(\cfrac{16}{7})-2\times 1=2-2\times 1=0\)，\(a_4=2\)；
\(b_5=a_5-2a_4=INT(\cfrac{32}{7})-2\times 2=4-4=0\)，\(a_5=4\)；
\(b_6=a_6-2a_5=INT(\cfrac{64}{7})-2\times 4=9-8=1\)，\(a_6=9\)；
故数列\(\{b_n\}\)为\(T=3\)的周期数列，故\(b_{2019}=b_{672\times3+3}=b_3=1\)；
解答题
例17【2019届宝鸡理数质检Ⅲ第17题】已知\(\vec{a}=(\sqrt{3}cosx，cosx)\)，\(\vec{b}=(sinx，cosx)\)，函数\(f(x)=\vec{a}\cdot \vec{b}\)，
(1).求\(f(x)\)的最小正周期和对称轴方程；
分析：\(f(x)=\vec{a}\cdot \vec{b}=\cdots =sin(2x+\cfrac{\pi}{6})+\cfrac{1}{2}\)，故\(T=\pi\)；
令\(2x+\cfrac{\pi}{6}=k\pi+\cfrac{\pi}{2}\)，得到对称轴方程为\(x=\cfrac{k\pi}{2}+\cfrac{\pi}{6}\)，\(k\in Z\)；
(2).当\(x\in (-\pi，\pi]\)时，求\(f(x)\)的单调递增区间；
法1：见图片解析；
法2：由于\(x\in (-\pi，\pi]\)，求得\(2x+\cfrac{\pi}{6}\in (-2\pi+\cfrac{\pi}{6}，2\pi+\cfrac{\pi}{6}]\)，
以\(2x+\cfrac{\pi}{6}\)为横轴，作出图像，由图像可知，当
例18【2019届宝鸡理数质检Ⅲ第18题】如图所示的多面体中，\(ABCD\)为菱形，\(BDEF\)为矩形，\(DE\perp\)平面\(ABCD\)，\(\angle BAD=\cfrac{\pi}{3}\)，\(AD=2\)，\(DE=\sqrt{3}\)，
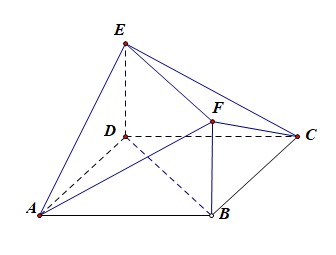
（1）求证：平面\(AEF\perp\)平面\(CEF\)；
法1：建立空间直角坐标系，利用空间向量法证明；如图，连结\(AC\)交\(BD\)于点\(O\)，取\(EF\)的中点为\(G\)，连结\(OG\)，分别以\(OA\)，\(OB\)，\(OG\)所在的直线为\(x\)，\(y\)，\(z\)轴建立直角坐标系，
由于\(DE\perp\)面\(ABCD\)，\(DE//FB\)，所以\(DE\perp AD\)，\(DE\perp CD\)，\(FB\perp BC\)，\(FB\perp AB\)，又\(ABCD\)为菱形，\(BDEF\)为矩形，则\(\triangle ADE\)，\(\triangle CDE\)，\(\triangle ABF\)，\(\triangle CBF\)是全等的直角三角形，
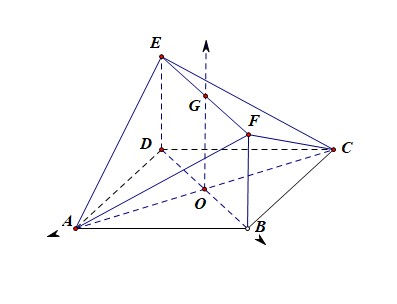
则由题目可知，\(A(\sqrt{3}，0，0)\)、\(A(\sqrt{3}，0，0)\)、\(B(0，1，0)\)、\(D(0，-1，0)\)、\(C(-\sqrt{3}，0，0)\)、\(E(0，-1，\sqrt{3})\)、\(F(0，1，\sqrt{3})\)，
则由\(\overrightarrow{AE}=(-\sqrt{3}，-1，\sqrt{3})\)，\(\overrightarrow{AF}=(-\sqrt{3}，1，\sqrt{3})\)，设平面\(AEF\)的法向量为\(\vec{n}=(x，y，z)\)，
则由\(\left\{\begin{array}{l}{-\sqrt{3}x-y+\sqrt{3}z=0}\\{-\sqrt{3}x+y+\sqrt{3}z=0}\end{array}\right.\)，求得\(\vec{n}=(1，0，1)\)；
由\(\overrightarrow{CE}=(\sqrt{3}，-1，\sqrt{3})\)，\(\overrightarrow{AF}=(\sqrt{3}，1，\sqrt{3})\)，设平面\(CEF\)的法向量为\(\vec{v}=(x，y，z)\)，
则由\(\left\{\begin{array}{l}{\sqrt{3}x-y+\sqrt{3}z=0}\\{\sqrt{3}x+y+\sqrt{3}z=0}\end{array}\right.\)，求得\(\vec{v}=(1，0，-1)\)；
由于\(\vec{n}\cdot \vec{v}=1+0-1=0\)，即两个平面的法向量垂直，故两个平面垂直，即平面\(AEF\perp\)平面\(CEF\)；
法2：面面垂直的定义法，设法证明其二面角为直二面角；连结\(AC\)交\(BD\)于点\(O\)，取\(EF\)的中点为\(G\)，连结\(OG\)，\(AG\)，\(CG\)，由于\(DE\perp\)面\(ABCD\)，\(DE//FB\)，所以\(DE\perp AD\)，\(DE\perp CD\)，\(FB\perp BC\)，\(FB\perp AB\)，又\(ABCD\)为菱形，\(BDEF\)为矩形，则\(\triangle ADE\)，\(\triangle CDE\)，\(\triangle ABF\)，\(\triangle CBF\)是全等的直角三角形，
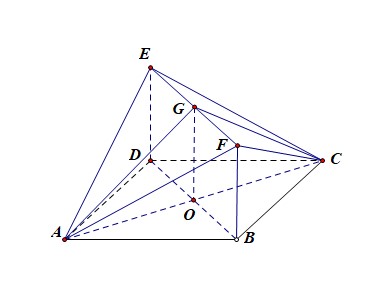
由\(AE=AF\)，\(CE=CF\)，\(G\)为\(EF\)的中点，可知\(AG\perp EF\)，\(CG\perp EF\)，则\(\angle AGC\)为二面角\(A-EF-C\)的平面角，由于\(AG=CG=\sqrt{6}\)，\(AC=2\sqrt{3}\)，故由勾股定理可知，\(\angle AGC=\cfrac{\pi}{2}\)，故平面\(AEF\perp\)平面\(CEF\)；
法3：立体几何法；待思考；
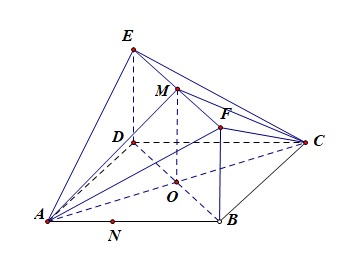
（2）在线段\(AB\)上取一点\(N\)，当二面角\(N-EF-C\)的大小为\(\cfrac{\pi}{3}\)时，求\(|AN|\)的长度；
如图，连结\(AC\)交\(BD\)于点\(O\)，取\(EF\)的中点为\(M\)，连结\(OM\)，分别以\(OA\)，\(OB\)，\(OM\)所在的直线为\(x\)，\(y\)，\(z\)轴建立直角坐标系，
例19【2019届宝鸡理数质检Ⅲ第19题】
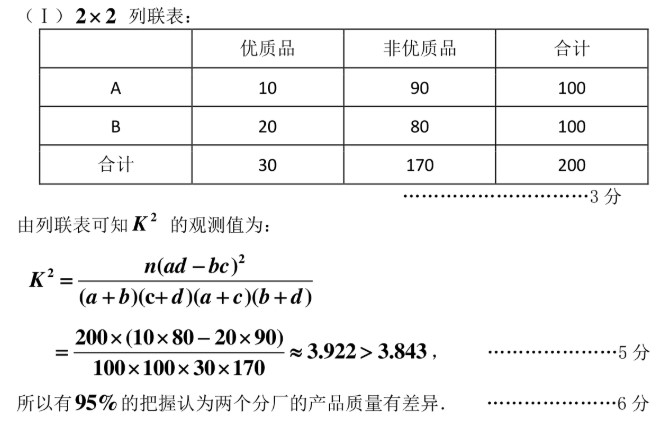
(Ⅰ)
(Ⅱ).ⅰ法1：采用条件概率定义法，设抽到一件产品是优质品为事件\(A\)，抽取的两件产品都是优质品为事件\(B\)，则需要求\(P(B|A)\)，
又\(P(A)=\cfrac{C_2^2+C_2^1C_8^1}{C_{10}^2}\)，\(P(AB)=\cfrac{C_2^2}{C_{10}^2}\)，
故\(P(B|A)=\cfrac{P(AB)}{P(A)}=\cfrac{\frac{C_2^2}{C_{10}^2}}{\frac{C_2^2+C_2^1C_8^1}{C_{10}^2}}=\cfrac{C_2^2}{C_2^2+C_2^1C_8^1}=\cfrac{1}{17}\)；
此法易错处：采用保底法，计算\(P(A)=\cfrac{C_2^1C_9^1}{C_{10}^2}\)，这是错误的，有重复，避免的方法是严格分类讨论即可。
ⅰ法2：采用古典概型法，从\(B\)厂的100个样本产品利用分层抽样的方法抽出10件产品中，优质品有2件，非优质品有8件，从这10件产品中随机抽取2件，其中抽到一件产品(暗含至少有一件)是优质品的事件有\(C_2^2+C_2^1C_8^1=17\)个，从这10件产品中随机抽取2件，抽取的都是优质品的事件有\(C_2^2=1\)个，所以在已知抽到一件产品是优质品的条件下，抽取的两件产品都是优质品的概率是\(\cfrac{1}{17}\)。
ⅱ用频率估计概率，从\(B\)分厂所有产品(总量有\(n\)件)中任取一件产品是优质品的概率为\(0.20\)，所以随机变量\(X\)服从二项分布，即\(X\sim B(10，0.20)\)，则\(E(X)=10\times 0.20=2\)。
此处易错：容易错判为超几何分布，此处注意，一则用频率估计概率，二则总量不知道，所以应该是二项分布；
例20【2019届宝鸡理数质检Ⅲ第20题】
例21【2019届宝鸡理数质检Ⅲ第21题】
选做题
例22【2019届宝鸡理数质检Ⅲ第22题】
(Ⅰ)求\(C\)的极坐标方程；
分析：消参，得到圆\(C\)的普通方程为\((x-2)^2+y^2=4\)，将\(x=\rho cos\theta\)，\(y=\rho sin\theta\)代入圆\(C\)的普通方程，化简整理得到\(C\)的极坐标方程为\(\rho=4cos\theta\)；
(Ⅱ)射线\(\theta=\theta_1\)，\((\theta_1\in [\cfrac{\pi}{6}]，\cfrac{\pi}{3}，\rho>0)\)与圆\(C\)的交点为\(O\)、\(P\)，与直线\(l\)的交点为\(Q\)，求\(|OP|\cdot |OQ|\)的取值范围。
分析：设\(P(\rho_1，\theta_1)\)，则有\(\rho_1=4cos\theta_1\)，
设\(Q(\rho_2，\theta_1)\)，又直线\(l\)的极坐标方程是\(\rho(\sqrt{3}sin\theta+cos\theta)=1\)，则\(\rho_2=\cfrac{1}{\sqrt{3}sin\theta_1+cos\theta_1}\)，
所以，\(|OP|\cdot |OQ|=\rho_1\rho_2=\cfrac{4cos\theta_1}{\sqrt{3}sin\theta_1+cos\theta_1}=\cfrac{4}{\sqrt{3}tan\theta_1+1}\)，
又\(\theta_1\in [\cfrac{\pi}{6}，\cfrac{\pi}{3}]\)，则\(tan\theta_1\in [\cfrac{\sqrt{3}}{3}，\sqrt{3}]\)，则\(1\leq |OP|\cdot |OQ|\leq 2\)，故\(|OP|\cdot |OQ|\)的取值范围为\([1，2]\).
解后反思：①经过极点的线段，其长度用极坐标表示比用直角坐标表示有更大的优越性。②当题目中出现线段和或者线段积时，采用极坐标思考和运算要简单的多。
例23【2019届宝鸡理数质检Ⅲ第23题】
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
