字符串的排列以及八皇后问题

2019独角兽企业重金招聘Python工程师标准>>>

题目：输入一个字符串，打印出该字符串中字符的所有排列。例如输入字符串 abc，则打印出由字符 a， b， c所能排列出的所有字符串 abc，acb，bac，bca，cab，cba。

对于这一个复杂问题，可以将其分解为若干个小问题。例如，我们把一个字符串 看成由两部分组成：第一部分是它的第一个字符，第二部分是后面的所有字符如下图，使用两种不同的背景颜色区分字符串的两部分。

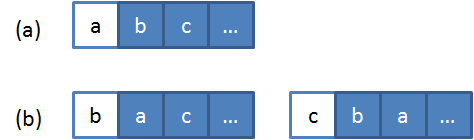
求整个字符串的排列，可以看成两步：首先求所有可能出现在第一个位置的字符，即把第一个字符和后面所有的字符交换。上图就是分别把第一个字符 a 和后面的 b， c 等字符交换的情形。第二步，固定第一个字符，求后面所有字符的排列。此时，仍将后面的字符分成两部分：后面字符的第一个字符，以及这个字符后面的所有字符。然后将第一个字符逐一和它后面的字符交换。【使用递归】

//字符串的排列
#include<iostream>
using namespace std;

void Permutation(char *pStr, char *pBegin)
{
 if(*pBegin == '\0')
 {
  printf("%s", pStr);
  cout << endl;
 }
 else
 {
  for(char *pCh = pBegin; *pCh != '\0'; pCh++)
  {

   char temp = *pBegin;
   *pBegin = *pCh;
   *pCh = temp;

   Permutation(pStr, pBegin + 1);

    temp = *pCh;
   *pCh = *pBegin;
   *pBegin = temp;

  }
 }
}

void StringPermutation(char *pStr)
{
 if(pStr == NULL)
  return;
 Permutation(pStr, pStr);
}

int main()
{
 
 char str[5] = "abcd";

 StringPermutation(str);

 system("pause");
 return 0;
}

Q：利用全排列解决八皇后问题：在 8 * 8的国际象棋上摆放 8 个皇后，使其不能相互攻击，即任意两个皇后不能处于同一行或同一列或同一对角线上。问，总共有多少种摆放方法。

由于 8 个皇后的任意两个不能处于同一行，那么肯定是每一个皇后占据一行，于是可以定义一个数组 ColumnIndex[8]， 数组中第 i 个数字表示位于第 i 行的皇后的列号。先把数组ColumnIndex 的 8个数字分别用 0~7 初始化，接下来就是对数组ColumnIndex 进行全排列。由于我们使用不同的数字初始化数组，所以任意两个皇后肯定是不同列。只需判断一个排列对应的 8 个皇后是不是位于同一个对角线上，也就是对于数组的两个下表 i 和 j 是不是 i - j = ColumnIndex[i] - ColumnIndex[j] 或者 j - i = ColumnIndex[i] - ColumnIndex[j]。

//字符串的排列
#include<iostream>
using namespace std;

int count = 0;

void Permutation(char *pStr, char *pBegin)
{
 if(*pBegin == '\0')
 {
  int flag = 0;
  for(int i = 0; i < 8; i++)
   for(int j = i + 1; j < 8; j++)
    if(i - j == pStr[i] - pStr[j] || j - i == pStr[i] - pStr[j])
    {
     flag = 1;
     break;
    }
  if(flag == 0)
  {
   count ++;
   printf("%s", pStr);
   cout << endl;
  }
 }
 else
 {
  for(char *pCh = pBegin; *pCh != '\0'; pCh++)
  {
   //cout <<"***pBegin: " << *pBegin << " ->" << "  pCh: " << *pCh << endl;
   char temp = *pBegin;
   *pBegin = *pCh;
   *pCh = temp;

   //cout <<"change ***pBegin: " << *pBegin << " ->" << "  pCh: " << *pCh << endl;

   Permutation(pStr, pBegin + 1);

   //cout <<"---pBegin: " << *pBegin << " ->" << "  pCh: " << *pCh << endl;

   temp = *pCh;
   *pCh = *pBegin;
   *pBegin = temp;

   //cout <<"change ---pBegin: " << *pBegin << " ->" << "  pCh: " << *pCh << endl;
  }
 }
}

void StringPermutation(char *pStr)
{
 if(pStr == NULL)
  return;
 Permutation(pStr, pStr);
}

int main()
{
 
 char str[9] = "01234567";

 StringPermutation(str);
 cout << count << endl;

 system("pause");
 return 0;
}

八皇后问题的另一种解决方案：

#include <stdio.h>
#include <stdlib.h>
#define max 8
int queen[max], sum=0; /* max为棋盘最大坐标 */

void show() /* 输出所有皇后的坐标 */
{
    int i;
    printf("");
    for(i = 0; i < max; i++)
    {
         printf(" %d", queen[i]);
    }
    printf("\n");
    sum++;
}
 
int PLACE(int n) /* 检查当前列能否放置皇后 */
{
    int i;
    for(i = 0; i < n; i++) /* 检查横排和对角线上是否可以放置皇后 */
    {
        if(queen[i] == queen[n] || abs(queen[i] - queen[n]) == (n - i))
        {
            return 1;
        }
    }
    return 0;
}
 
void NQUEENS(int n) /* 回溯尝试皇后位置,n为横坐标 */
{
    int i;
    for(i = 0; i < max; i++)
    {      
        queen[n] = i; /* 将皇后摆到当前循环到的位置 */
        if(!PLACE(n))
        {          
            if(n == max - 1)
            {
                show(); /* 如果全部摆好，则输出所有皇后的坐标 */
            }        
            else
            {
                NQUEENS(n + 1); /* 否则继续摆放下一个皇后 */
            }
        }
    }
}
 
int main()
{
    NQUEENS(0); /* 从横坐标为0开始依次尝试 */
    printf("%d", sum);
    system("pause");
    return 0;
}

 

 

转载于:https://my.oschina.net/u/2260265/blog/346392