《大数据分析原理与实践》一一3.1 回归分析

本节书摘来自华章计算机《大数据分析原理与实践》一书中的第3章，第3.1节,作者：王宏志 更多章节内容可以访问云栖社区“华章计算机”公众号查看。

3.1　回归分析

3.1.1　回归分析概述
1.回归分析的定义
回归分析方法是在众多的相关变量中，根据实际问题考察其中一个或多个变量（因变量）与其余变量（自变量）的依赖关系。如果只需考察一个变量与其余多个变量之间的相互依赖关系，我们称为多元回归问题。若要同时考察多个因变量与多个自变量之间的相互依赖关系，我们称为多因变量的多元回归问题。本小节重点讨论多元回归。
2.回归分析的数学模型
多元回归分析研究因变量Y与m个自变量x1，x2，…，xm的相关关系，而且总是假设因变量Y为随机变量，而x1，x2，…，xm为一般变量。
假定因变量Y与x1，x2，…，xm线性相关。收集到的n组数据（yt，xt1，xt

则所建回归模型的矩阵形式为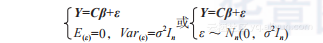

称它们为经典多元回归模型，其中Y是可观测的随机向量，ε是代表不可观测的随机向量和测量误差的随机变量，C是已知矩阵，β、σ2是未知参数，n为观测记录个数，m为模型中自变量个数，并设n＞m，C应为满秩矩阵且满足m+1≤n。
在经典回归分析中讨论模型中参数β=（β0，β1，…，βm）'和σ2的估计和检验问题。近代回归分析中讨论变量筛选、估计的改进，以及对模型中的一些假设进行诊断等问题。
3.回归分析的基本计算方法
这里概述回归分析的基本计算方法，关于大数据的回归算法在11.2节中讨论。回归分析的主要目的是估算回归系数β的值。最常用的方法采取最小二乘估计法OLS。
若C为满秩，m+1≤n，则β的OLS估计为：，其求值的计算过程为y→C'→C'C→(C'C)-1→C'y。
于是，拟合得到方程为为预测值（拟合值），H是帽子矩阵，H=C(C'C)-1 C'，其残差为：（性质：）。
残差平方和：ε'ε。
如果C不为满秩，则用（C'C）-代替（C'C）-1，（C'C）-为（C'C）-1广义逆。
4.回归分析的模型检验
回归分析的模型检验用于检验模型的可用性，模型检验的过程可以分为三个步骤，即分析模型拟合优度、分析模型是否能用于预测未知值和分析模型的解释变量成员显著性检验。
（1）拟合优度检验
拟合优度是回归模型整体的拟合度，表达因变量与所有自变量之间的总体关系。拟合优度检验是用于检验来自总体中一类数据的分布是否与某种理论分布相一致的统计方法。具体来说，对于观察值y1，y2，…，yn，利用得到的回归模型估计出的yi为，，则拟合优度可以用如下参数进行计算。
SSR（回归平方和）：y的估计值和均值的平方和，即SSR=。
SSE（剩余平方和）：y残差（真值和估计值之差）的平方和，即SSE=。
SST总离差平方和：SST==SSR+SSE。
根据上述参数计算决定系数来判断拟合优度，即解释变量在预测y中所做的贡献的比例

R2于[0，1]之间，越接近1，拟合越好；反之，拟合的优度越低。
为了做出更优的判断，可以进一步调整决定系数如下：

n为记录的个数，m为自变量个数，其具体意义同R2。
（2）残差分析
残差指的是真实Y值和预测Y值之间的差。残差分析就是通过计算残差的特征来检验回归模型的质量。残差分析其基本出发点是，如果得到的回归模型能够较好地反映Y的特征和变化规律，那么残差项应该没有明显的趋势性和规律性，即残差序列独立且满足均值为0，方差相同的正态分布。下面依次介绍残差性质的判定方法。
1）判断残差是否为总体服从均值为0的正态分布。
正态性可以通过画残差图来描述，其横轴为因变量，纵轴为残差值，若点在纵轴为0的横线上下随机散落，说明残差有正态性。
需要注意的是，若残差的协方差矩阵诸对角元的杠杆率有很大差别，诸残差就会有很大变化，一般会用学生化残差代替残差。我们预期学生化残差大致看上去像是从标准正态分布中抽取的独立样本。
学生化残差：
残差均方：
其中，hjj为杠杆率，即C（C'C）-1C的（i，j）对角元，。
杠杆率
由于离群值可能对拟合效果起着重要作用，因此要判断某个值对参数C的估计影响是否过大。杠杆率是判断第j个数据点到其他n-1个数据点的距离的度量，若某杠杆率相对于其他的要大，则说明这个数据对相应的参数估计值有主要贡献，即去掉这个值后，参数估计矩阵变化很大，所以杠杆率大小差不多时，我们可以用拟合的回归方程做预测，并在某种程度上保证不会被误导。

2）判断残差独立性。
残差的独立性可以通过判断残差的自相关实现，也就是说，随着时间推移，残差呈现有规律变化，则说明残差不独立。残差独立性可以通过自相关系数来检验。自相关系数定义为

ρ取值范围为（-1，+1），它的值越接近1，则说明存在正相关关系，越接近-1，说明有负相关关系，等于0则说明残差序列无自相关。
另一种方法是DW（Durbin-Watson）检验，这是统计分析中经典的检验序列一阶自相关最常用的方法，检验值r1取值范围是（0，4），定义为。
r1=0时，残差序列存在完全正自相关；r1的值在区间（0，2）中时，残差序列存在正自相关；r1=2时，残差序列无自相关；r1的值在区间（2，4）中时，残差序列存在负自相关；r1=4时，残差序列存在完全负自相关。
若残差存在自相关，说明回归方程没能充分说明因变量的变化规律，也就是方程中遗漏了一些较为重要的自变量，或者变量存在滞后性（过去的性质，现在才体现），或者回归模型选择不合适，不应选线性模型等。
3）残差的方差相等判定。
这种方法的出发点是，无论自变量怎么取值，残差的方差不应有所改变，否则认为出现异方差。该性质可以通过如下两种方法判断：
残差图：判断随着自变量增加，残差的方差是否呈现增加或减少的趋势。
Spearman等级相关分析：检验统计量的概率值P是否小于给定的显著性水平，若小于，则拒绝原假设（自变量与残差存在显著相关），从而说明残差出现异方差。Spearman等级相关可以用度量定序（可以非定距）变量间的相关关系，其计算系数r和2.2.2节中介绍的皮尔森系数类似，只是用两变量的秩（Ui，Vi）代替（xi，yi）求出r，即

其假设检验步骤用标准正态分布Z检验，其步骤同第2章介绍的t检验类似，即给定α值，计算z值，然后判断显著性，即

若|z|＜Zα/2，说明此时P值小于α（默认0.05），说明线性显著，否则不显著。
请注意，所有跟检验相关的计算中，α默认0.05，也可自定义。这表明拒绝原假设的阈值，意味着P值小于α，则拒绝原假设，相当于表明一种显著关系。
（3）变量相关性
可以用假设检验判断上述线性结果是否表现显著。
皮尔森用t检验统计量进行检验。r服从t（n-2）分布，n-2为分布的自由度。判断过程如下：
给定显著性水平α（一般α=0.05），计算t值：

若|t|＜tα/2（n-2），则其P值就会小于0.05，说明存在显著线性相关；反之，说明线性相关不明显。
（4）判断模型中自变量对Y线性相关的显著性
该方法首先判断所有X对Y的影响的显著性，再依次判断每个自变量X对Y的影响的显著性。
可