转载请注明出处:http://www.cnblogs.com/Peyton-Li/
逻辑回归名字听起来像是做处理回归问题的,其实不然,逻辑回归是分类模型,可以被看作是一个非常小的神经网络。
二项逻辑回归模型是如下的条件概率分布:
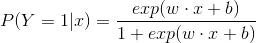
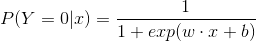
这里,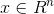 是输入,
是输入,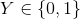 是输出,
是输出,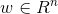 和
和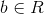 是参数,
是参数,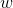 称为权值向量,
称为权值向量,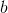 称为偏置,
称为偏置,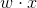 为
为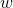 和
和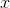 的内积。
的内积。
对于给定的输入实例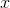 ,按照上面两式可以求得
,按照上面两式可以求得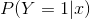 和
和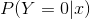 ,逻辑回归模型比较两个条件概率值的大小,将实例
,逻辑回归模型比较两个条件概率值的大小,将实例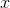 分到概率值较大的那一类。
分到概率值较大的那一类。
有时为了方便,将权值向量和输入向量加以扩充,仍记作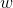 ,
,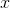 ,即
,即
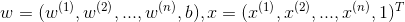
这时,逻辑回归模型如下:
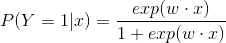
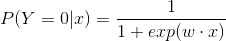
我们一般使用极大似然估计法估计模型参数,
似然函数为:
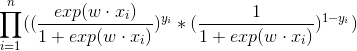
对数似然函数为:
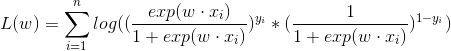
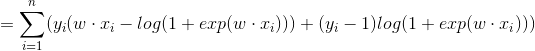
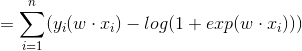
对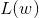 求最大值,得到
求最大值,得到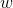 的估计值。
的估计值。
逻辑回归学习中,通常采用的方法是梯度下降法和拟牛顿法。
假设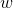 的极大似然估计值是
的极大似然估计值是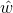 ,那么学到的逻辑回归模型为:
,那么学到的逻辑回归模型为:
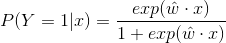
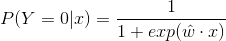
假设离散型随机变量Y的取值集合为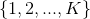 ,那么多项逻辑回归模型是:
,那么多项逻辑回归模型是:
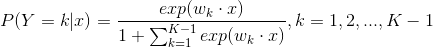
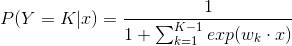
这里,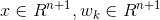







 本文介绍了逻辑回归的基本原理,包括其作为分类模型的应用,并详细解释了二项逻辑回归模型及多项逻辑回归模型的数学表达形式。此外,还介绍了模型参数的估计方法,如极大似然估计法及其对应的梯度下降法和拟牛顿法。
本文介绍了逻辑回归的基本原理,包括其作为分类模型的应用,并详细解释了二项逻辑回归模型及多项逻辑回归模型的数学表达形式。此外,还介绍了模型参数的估计方法,如极大似然估计法及其对应的梯度下降法和拟牛顿法。
















 1532
1532

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








