320. Generalized Abbreviation-- back tracking and bit manipulation(待续)

最新推荐文章于 2019-08-16 17:02:24 发布

转载最新推荐文章于 2019-08-16 17:02:24 发布 · 55 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/keepAC/p/9944641.html

本文探讨了一种将字符串中字母转换为数字的算法，通过递归实现所有可能的组合，并解决了一个特定问题：如何在不违反规则的情况下，将任意长度的字符串转换成包含数字的组合。文章还提供了一种使用位操作的替代解决方案。

把一个字符串中字母用数字代替，产生所有的组合数
Input: "word"
Output:
["word", "1ord", "w1rd", "wo1d", "wor1", "2rd", "w2d", "wo2", "1o1d", "1or1", "w1r1", "1o2", "2r1", "3d", "w3", "4"]

和78 subsets本质上也是一样的： https://leetcode.com/problems/subsets/description/

画出递归数吧： 假设word = "abc", 递归数如下：

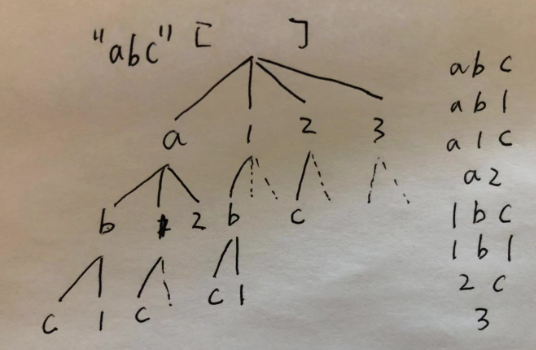
需要注意的是，如果某个节点已经是数字了，则接下来不能继续放数字，例如 "a11" 是不合法的。

先写了如下code ，在 input = "interaction" 时WA了，而其他短字符串都可以过。

因为最后一行 “curResult.deleteCharAt(curResult.length()-1);” input 字符串长度超过10后，每次加的长度就是2位数了，所以不能只减去1。

class Solution {
    public List<String> generateAbbreviations(String word) {
        List<String> result = new ArrayList<>();
        
        dfs(new StringBuilder(), result, word,0);
        return result;
    }
    
    private void dfs(StringBuilder curResult,List<String> result, String word, int cur_index){
        if(curResult.length() == word.length() || cur_index == word.length()){
            result.add(curResult.toString());
            return;
        }
        
        // put cur letter
        curResult.append(word.charAt(cur_index));
        dfs(curResult,result, word,cur_index+1);
        curResult.deleteCharAt(curResult.length()-1);
        
        for(int i=1; i<=word.length()-cur_index; i++){ // wrd: cur_index = 0, len =3, 可以放 1，2,3
            // 当前result 里 最后一个字符得是字母才能 放数字
            if(curResult.length()==0 || Character.isLetter(curResult.charAt(curResult.length()-1)) ){
                curResult.append(i);
                dfs(curResult,result,word,cur_index+i);
                curResult.deleteCharAt(curResult.length()-1);
            }
            
        }
    }
    
    
}

修改后的code, 每次记录上一次的stringbuild 长度，然后重新setLeng 到之前的长度即可:

class Solution {
    public List<String> generateAbbreviations(String word) {
        List<String> result = new ArrayList<>();
        dfs(new StringBuilder(), result, word,0);
        return result;
    }
    
    private void dfs(StringBuilder curResult,List<String> result, String word, int cur_index){
        if(curResult.length() == word.length() || cur_index == word.length()){
            result.add(curResult.toString());
            return;
        }
       
        int len = curResult.length(); // 每次记录长度
        // put cur letter
        curResult.append(word.charAt(cur_index));
        dfs(curResult,result, word,cur_index+1);
        curResult.setLength(len);
        //put the 剩下的可能的长度
        for(int i=1; i<=word.length()-cur_index; i++){ // wrd: cur_index = 0, len =3, 可以放 1，2,3
            // 当前result 里 最后一个字符得是字母才能 放数字
            if(curResult.length()==0 || Character.isLetter(curResult.charAt(curResult.length()-1)) ){
                curResult.append(i);
                dfs(curResult,result,word,cur_index+i);
                curResult.setLength(len); //恢复之前的长度
            }   
        }
    }  
}

这道题还可以用  bit manipulation 来解， 如下：

m a n i p u l a t i o n
m  2  i p      6      n
1 0 0 1 1 0 0 0 0 0 0 1

转载于:https://www.cnblogs.com/keepAC/p/9944641.html