暑假集训8.6数论专题—Savage(扩展欧几里得算法)

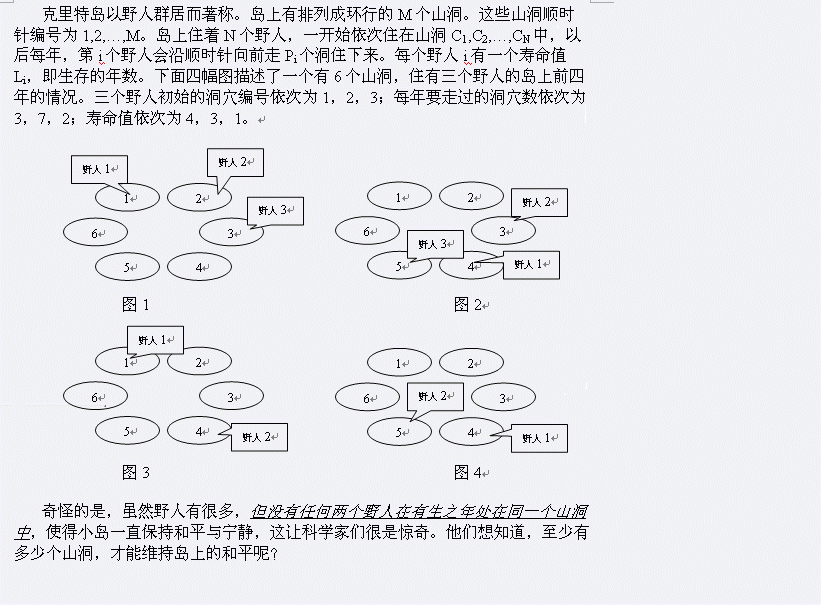
题目描述：

Input

  第1行为一个整数N(1<=N<=15)，即野人的数目。

第2行到第N+1每行为三个整数Ci, Pi, Li表示每个野人所住的初始洞穴编号，每年走过的洞穴数及寿命值。

(1<=Ci,Pi<=100, 0<=Li<=10^6 ) 

 

Output

仅包含一个数M，即最少可能的山洞数。输入数据保证有解，且M不大于10^6。

 

题解：

 因为围成一个环因此能想到mod，接着我们可以你逆向思考，当ci+pi*x≡cj+pj*x(mod ans)存在时，ans不合法，由于数据较小，且不满足二分性质，我们可以由小到大枚举ans的大小，将式子化成(pi-pj)*x+ans*y=cj-ci，根据这个式子可以用扩展欧几里得解除x，根据x与li,lj的关系判断x是否合法。

 

关于扩展欧几里得：

上板子！

LL exgcd(LL a,LL b,LL &x,LL &y){
    if(b==0){x=1;y=0;return a;}
    LL t=exgcd(b,a%b,x,y);LL x1=x;
    x=y;y=x1-a/b*y;
    return t;
}

View Code

整题完整代码如下：

#include<bits/stdc++.h>
#define il inline
#define LL long long
#define _(d) while(d(isdigit(ch=getchar())))
using namespace std;
const int N=17;
int n,p[N],c[N],l[N],m;
il int read(){int x,f=1;char ch;_(!)ch=='-'?f=-1:f;x=ch-48;_()x=x*10+ch-48;return f*x;}
LL exgcd(LL a,LL b,LL &x,LL &y){
    if(b==0){x=1;y=0;return a;}
    LL t=exgcd(b,a%b,x,y);
    LL x1=x;x=y;y=x1-a/b*y;return t;
}
il bool check(LL m){
    LL x,y,g;
    for(int i=1;i<=n;i++)
        for(int j=i+1;j<=n;j++){
            g=exgcd((LL)(p[i]-p[j]),m,x,y);
            if(((c[j]-c[i])%g+g)%g)continue;
            x=x*(LL)(c[j]-c[i])/g;g=abs(g);
            x=(x%(m/g)+(m/g))%(m/g);
            if(x<=l[i]&&x<=l[j])return 0;
        }
    return 1;
}
int main()
{
    n=read();for(int i=1;i<=n;i++)c[i]=read(),p[i]=read(),l[i]=read(),m=max(m,c[i]);
    while(!check((LL)m))m++;printf("%d\n",m);
  return 0;
}

View Code

 

转载于:https://www.cnblogs.com/Jessie-/p/9434449.html