函数图像的辨析

前言

函数图像的识别、辨析问题，常考查函数的奇偶性，函数值的正负、单调性、对称性、零点、极限、极值等，常用排除法；其一般的步骤是：定义域；值域；周期性；奇偶性；确定单调区间，极值点等；求函数的某些特殊点，如与坐标轴的交点，不连续点；考察渐近线；

典例剖析

例1【2019高三理科数学启动卷，2019陕西省二检试卷第7题】已知函数\(f(x)=x^2-e^{|x-1|}-2x+3\)，则\(f(x)\)的大致图像是【】

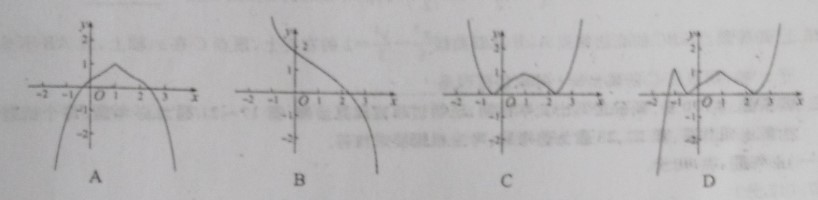
分析：为求作函数\(f(x)=x^2-e^{|x-1|}-2x+3=(x-1)^2-e^{|x-1|}+2\)的图像，选函数\(g(x)=x^2-e^{|x|}+2\)为模板函数，偶函数，故函数\(f(x)\)的图像关于直线\(x=1\)对称，故排除\(B\)和\(D\)，再用赋值法，\(f(3)=3^2-e^2-6+3<0\)，则排除\(C\)，故选\(D\)。

例2【2019高三理科数学三轮模拟试题】已知函数\(f(x)=e^|x|\cdot cosx\)，则\(f(x)\)的大致图像是【】

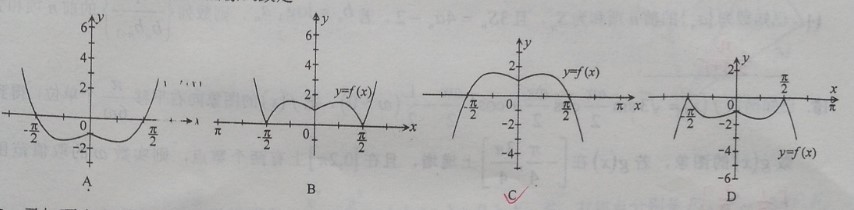
分析：函数\(f(x)\)为偶函数，结合赋值法，选\(C\).

转载于:https://www.cnblogs.com/wanghai0666/p/10818120.html