全排列 Permutations

为什么80%的码农都做不了架构师？>>>   

问题：

Given a collection of distinct numbers, return all possible permutations.

For example,
[1,2,3] have the following permutations:

[
  [1,2,3],
  [1,3,2],
  [2,1,3],
  [2,3,1],
  [3,1,2],
  [3,2,1]
]

解决：

【注】全排列的实现，以123为例：

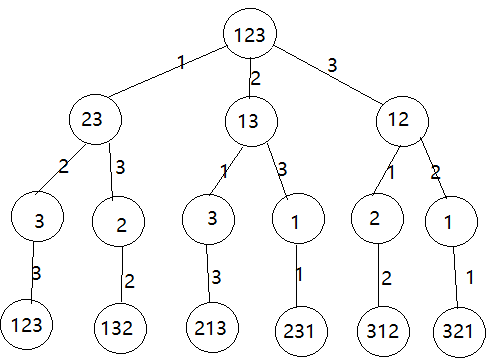
① 题目要求列出数组的全排列。使用递归（回溯）方法。用DFS，时间 O(N^2) 空间 O(N)。

以[1，3，5，9]的全排列为例：

第一个：1，3，5，9.（保存不变）
首先保持1不变，对3，5，9 进行全排列。同样地，我们先保持3不变，对5，9 进行全排列。保持5不变，对9对进行全排列，由于9只有一个，它的排列只有一种：9。
接下来不能以5 打头了，5，9 相互交换，得到
1，3，9，5.
此时5，9 的情况都写完了，不能以3打头了，得到
1，5，3，9
1，5，9，3
1，9，3，5
1，9，5，3

我们就得到了1开头的所有排列，这是我们一般的排列数生成的过程。再接着是以3、5、9 打头，得到全排列。这里还要注意的一点是，对于我们人而言，我们脑子里相当于是储存了一张表示原有数组的表，1，3，5，9，1 开头的所有排列完成后，我们选择3 开头，3 选完了之后，我们选择5 开头，而不会再返过来选1，而且知道选到9 之后结束，但对于计算机而言，我们得到了3，5，1，9 后，可能再次跳到1 当中，因为原来数组的顺序它已经不知道了，这样便产生了错误。对于算法的设计，我们也可以维护这样一个数组，它保
存了原始的数据，这是一种方法。同时我们还可以再每次交换后再交换回来，变回原来的数组，这样程序在遍历的时候便不会出错。

以上方法可以总结为：任意选一个数（一般从小到大或者从左到右）打头，对后面的n-1 个数进行全排列。

这是一个递归的方法，因为要得到n-1 个数的全排列，我们又要先去得到n-2 个数的全排列，而出口是只有1 个数的全排列，因为它只有1 种，为它的本身。

写成比较规范的流程：

1.开始for 循环。
2.改变第一个元素为原始数组的第一个元素（什么都没做）。
3.求第2个元素到第n个元素的全排列。
4.要求第2个元素到第n个元素的全排列，要递归的求第3个元素到第n个元素的全排列。
......
5.直到递归到第n个元素到第n元素的全排列，递归出口。
6.将改变的数组变回。
7.改变第一个元素为原始数组的第二个元素。
5.求第2个元素到第n个元素的全排列。
6.要求第2个元素到第n个元素的全排列，要递归的求第3 个元素到第n个元素的全排列。
......
5.直到递归到第n 个元素到第n 元素的全排列，递归出口。
6.将改变的数组变回。
......
8.不断地改变第一个元素，直至n次使for循环中止

class Solution { //5ms
    public List<List<Integer>> permute(int[] nums) {
        List<List<Integer>> res = new ArrayList<>();
        dfs(nums,0,res);
        return res;
    }
    public void dfs(int[] nums,int i,List<List<Integer>> res){//i表示当前排列的开头在原固定数组中的位置，即是否交换到了最后一个位置
        //找到转换完成的链表，将其存入链表中
        if(i == nums.length - 1){//递归结束条件，得到一个排列
            List<Integer> tmp = new ArrayList<>();
            for (int j = 0;j < nums.length ;j ++ ) {
                tmp.add(nums[j]);
            }
            res.add(tmp);
        }
        // 将当前位置的数跟后面的数交换，并搜索解
        for (int j = i;j < nums.length ;j ++ ) {
            swap(nums,i,j); //交换开头，若j=i表示固定当前开头计算排列，否则表示以当前值为开头的已经排列完了
            dfs(nums,i + 1,res);//改变数组的开头为原数组中i之后的第一个数，递归得到它的全排列
            swap(nums,i,j);//递归完成，还原交换的数组
        }
    }
    public void swap(int[] nums,int i,int j){
        int tmp = nums[i];
        nums[i] = nums[j];
        nums[j] = tmp;
    }
}

② 我们还可以简单的使用DFS来解决这题。使用一个专门的链表pre记录当前遍历到的排列，每一轮搜索选择一个数加入链表中，同时我们还要维护一个全局的布尔数组，来标记哪些元素已经被加入链表了，这样在下一轮搜索中要跳过这些元素。时间 O(N) 空间 O(N) 

class Solution { //6ms
    public List<List<Integer>> permute(int[] nums) {
        List<List<Integer>> res = new ArrayList<>();
        List<Integer> pre = new ArrayList<>();
        boolean[] used = new boolean[nums.length];
        dfs(nums,used,pre,res);
        return res;
    }
    public void dfs(int[] nums,boolean[] used,List<Integer> pre,List<List<Integer>> res){
        if(pre.size() == nums.length){
            res.add(new ArrayList<>(pre));
            return;
        }
        for (int i = 0;i < nums.length;i ++ ) {
            if(! used[i]){//若当前值没有被加入过，加入到链表中
                pre.add(nums[i]);
                used[i] = true;
                dfs(nums,used,pre,res);
                pre.remove(pre.size() - 1);
                used[i] = false;
            }
        }
    }
}

转载于:https://my.oschina.net/liyurong/blog/1528710