Algs4-1.4.22仅用加减实现的二分查找(Mihai Patrascu)

1.4.22仅用加减实现的二分查找(Mihai Patrascu)。编写一个程序，给定一个含有N个不同int值的按照升序排列的数组，判断它是否含有给定的整数。只能使用加法和减法以及常数的额外内存空间。程序运行时间在最坏情况下应该和logN成正比。
答：用斐波纳契数代替2的幂(二分法)进行查找。用两个变量保存Fk和Fk-1并在[i,i+Fk]之间查找。在每一步中，使用减法计算Fk-2，检查i+Fk-2处的元素，根据结果将搜索范围变为[i,i+Fk-2]或是[i+Fk-2,i+Fk-2+Fk-1]。
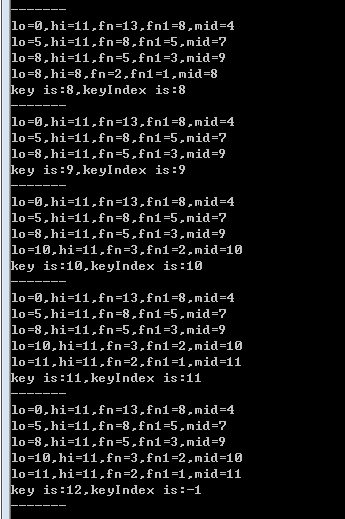
答：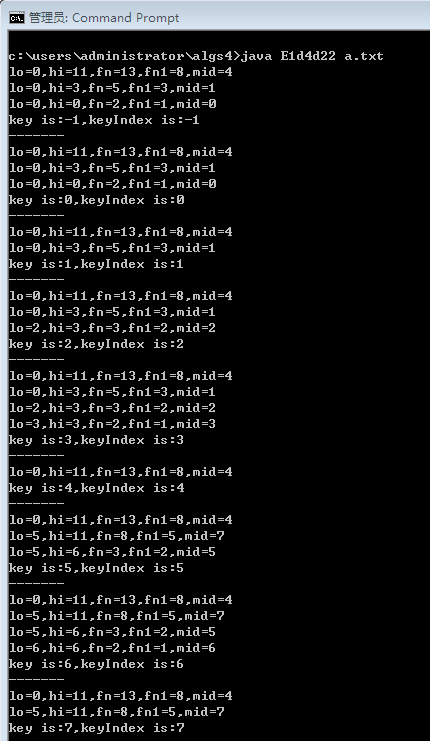








import java.util.Arrays;
public class E1d4d22
{
    public static void main(String[] args)
    {
        int[] a=In.readInts(args[0]);
        int keyIndex;
        for(int key=-1;key<=a.length;key++)
            {
              keyIndex=rank(a,key);
              StdOut.printf("key is:%d,keyIndex is:%d\n",key,keyIndex);
              StdOut.println("-------");
            }
    }
   
    public static int rank(int[] a,int key)
    {
        int fn1=1;
        int fn=1;
        while(fn<a.length)
        {
            fn=fn+fn1;
            fn1=fn-fn1;
        }
        //
        int lo=0;
        int hi=a.length-1;
        int mid;
        while(lo<=hi)
        {
            mid=lo+(fn-fn1)-1;
            StdOut.printf("lo=%d,hi=%d,fn=%d,fn1=%d,mid=%d\n",lo,hi,fn,fn1,mid);
            if(key<a[mid])
            {
                hi=mid-1;
                fn=fn-fn1;
                fn1=fn1-fn;
             }
            else if(key>a[mid])
            {
                lo=mid+1;
                fn1=fn-fn1;
                fn=fn-fn1;
            }
            else
               return mid;
        }//end while
         return -1;
   }//end rank
}//end class

转载于:https://www.cnblogs.com/longjin2018/p/9854456.html