2的正幂末尾数的模式

最新推荐文章于 2024-07-19 22:20:55 发布

weixin_34113237

最新推荐文章于 2024-07-19 22:20:55 发布

阅读量367

点赞数

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/sirlipeng/p/5391096.html

2的正幂 — 2, 4, 8, 16, 32, 64, 128, 256, … — 末尾数字遵循一个显而易见的规律: 2, 4, 8, 6, 2, 4, 8, 6, … . 这4个数字永远循环下去。最末尾数以外还有循环 — 实际上是最末m位 — 从2^m 开始的2的幂。例如，从04开始最末两位数就存在一个长度20的循环，同时从008开始最末3位数就存在一个长度100的循环。

本文，我将告诉你为什么会有这些循环，它们有多长，如何表达为数学形式，如何看见它们。

最末尾数的循环

末位数-所在位置-是十进制整数d在d/10后的余数。等价地，末位数是d mod 10的结果，根据约定取最小非负值-普通余数-作为返回结果。模运算，持续叠加到2的幂运算，得到末位数的循环：

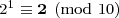
$\mbox{\footnotesize{\displaystyle{2^1 \equiv \textbf{2} \pmod{10}}}}$
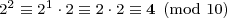
$\mbox{\footnotesize{\displaystyle{2^2 \equiv 2^1 \cdot 2 \equiv 2 \cdot 2 \equiv \textbf{4} \pmod{10}}}}$
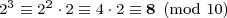
$\mbox{\footnotesize{\displaystyle{2^3 \equiv 2^2 \cdot 2 \equiv 4 \cdot 2 \equiv \textbf{8} \pmod{10}}}}$
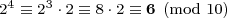
$\mbox{\footnotesize{\displaystyle{2^4 \equiv 2^3 \cdot 2 \equiv 8 \cdot 2 \equiv \textbf{6} \pmod{10}}}}$
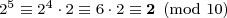
$\mbox{\footnotesize{\displaystyle{2^5 \equiv 2^4 \cdot 2 \equiv 6 \cdot 2 \equiv \textbf{2} \pmod{10}}}}$
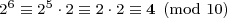
$\mbox{\footnotesize{\displaystyle{2^6 \equiv 2^5 \cdot 2 \equiv 2 \cdot 2 \equiv \textbf{4} \pmod{10}}}}$
…

我们从2开始，取10的模，再乘以2，再对10取模，等等。可知此模式将循环，直到先前的一个结果-2再次出现在第五步-循环确认。这展现了数字 2ⁿ, n ≥ 1, 末位数在四个数字 2, 4, 8, 和 6间循环。

这循环告诉我们，末尾数相同的2的幂是有关联的，它们的指数相差4：

Ends in 2: 2¹, 2⁵, 2⁹, 2¹³, 2¹⁷, … .
Ends in 4: 2², 2⁶, 2¹⁰, 2¹⁴, 2¹⁸, … .
Ends in 8: 2³, 2⁷, 2¹¹, 2¹⁵, 2¹⁹, … .
Ends in 6: 2⁴, 2⁸, 2¹², 2¹⁶, 2²⁰, … .

你可以使用指数运算规则来更简洁地描述，展示所有2的幂中末位数有规律的前4个：

Ends in 2: 2¹·2^4k, or 2^1+4k, k ≥ 0.
Ends in 4: 2²·2^4k, or 2^2+4k, k ≥ 0.
Ends in 8: 2³·2^4k, or 2^3+4k, k ≥ 0.
Ends in 6: 2⁴·2^4k, or 2^4+4k, k ≥ 0.

也可以按照指数对4取模的结果来对2的幂建立联系：

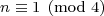
Ends in 2: $\mbox{\footnotesize{\displaystyle{n \equiv 1 \pmod{4}}}}$
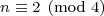
Ends in 4: $\mbox{\footnotesize{\displaystyle{n \equiv 2 \pmod{4}}}}$
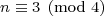
Ends in 8: $\mbox{\footnotesize{\displaystyle{n \equiv 3 \pmod{4}}}}$
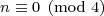
Ends in 6: $\mbox{\footnotesize{\displaystyle{n \equiv 0 \pmod{4}}}}$

这就很容易知道任意2的正幂的末位数是几。例如， 2³¹⁹ 的末位数是 8, 因为 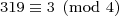$\mbox{\footnotesize{\displaystyle{319 \equiv 3 \pmod{4}}}}$ .

**Cycle in the Last Digit of 2ⁿ, n≥1**
Power of Two (k ≥ 0)	Exponent (mod 4)	Last Digit
2^1+4k	1	2
2^2+4k	2	4
2^3+4k	3	8
2^4+4k	0	6

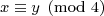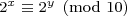小结，表格告诉我们，如果 $\mbox{\footnotesize{\displaystyle{x \equiv y \pmod{4}}}}$ , $\mbox{\footnotesize{\displaystyle{2^x \equiv 2^y \pmod{10}}}}$ .

末两位数的循环

类似的分析，只是对100取模，展示2的幂的末两位数，从 2²开始，循环周期是20:

**Cycle in the Last Two Digits of 2ⁿ, n≥2**
Power of Two (k ≥ 0)	Exponent (mod 20)	Last 2 Digits
2^2+20k	2	04
2^3+20k	3	08
2^4+20k	4	16
2^5+20k	5	32
2^6+20k	6	64
2^7+20k	7	28
2^8+20k	8	56
2^9+20k	9	12
2^10+20k	10	24
2^11+20k	11	48
2^12+20k	12	96
2^13+20k	13	92
2^14+20k	14	84
2^15+20k	15	68
2^16+20k	16	36
2^17+20k	17	72
2^18+20k	18	44
2^19+20k	19	88
2^20+20k	0	76
2^21+20k	1	52

末三位的循环

为了找出末三位数的循环，重复上面的过程，对1000取模。下面展示了2的幂的末三位，从 2³开始，循环周期是100：

**Cycle in the Last Three Digits of 2ⁿ, n≥3**
Power of Two (k ≥ 0)	Exponent (mod 100)	Last 3 Digits
2^3+100k	3	008
2^4+100k	4	016
2^5+100k	5	032
2^6+100k	6	064
2^7+100k	7	128
2^8+100k	8	256
2^9+100k	9	512
2^10+100k	10	024
2^11+100k	11	048
2^12+100k	12	096
2^13+100k	13	192
2^14+100k	14	384
2^15+100k	15	768
2^16+100k	16	536
2^17+100k	17	072
2^18+100k	18	144
2^19+100k	19	288
2^20+100k	20	576
2^21+100k	21	152
2^22+100k	22	304
2^23+100k	23	608
2^24+100k	24	216
2^25+100k	25	432
2^26+100k	26	864
2^27+100k	27	728
2^28+100k	28	456
2^29+100k	29	912
2^30+100k	30	824
2^31+100k	31	648
2^32+100k	32	296
2^33+100k	33	592
2^34+100k	34	184
2^35+100k	35	368
2^36+100k	36	736
2^37+100k	37	472
2^38+100k	38	944
2^39+100k	39	888
2^40+100k	40	776
2^41+100k	41	552
2^42+100k	42	104
2^43+100k	43	208
2^44+100k	44	416
2^45+100k	45	832
2^46+100k	46	664
2^47+100k	47	328
2^48+100k	48	656
2^49+100k	49	312
2^50+100k	50	624
2^51+100k	51	248
2^52+100k	52	496
2^53+100k	53	992
2^54+100k	54	984
2^55+100k	55	968
2^56+100k	56	936
2^57+100k	57	872
2^58+100k	58	744
2^59+100k	59	488
2^60+100k	60	976
2^61+100k	61	952
2^62+100k	62	904
2^63+100k	63	808
2^64+100k	64	616
2^65+100k	65	232
2^66+100k	66	464
2^67+100k	67	928
2^68+100k	68	856
2^69+100k	69	712
2^70+100k	70	424
2^71+100k	71	848
2^72+100k	72	696
2^73+100k	73	392
2^74+100k	74	784
2^75+100k	75	568
2^76+100k	76	136
2^77+100k	77	272
2^78+100k	78	544
2^79+100k	79	088
2^80+100k	80	176
2^81+100k	81	352
2^82+100k	82	704
2^83+100k	83	408
2^84+100k	84	816
2^85+100k	85	632
2^86+100k	86	264
2^87+100k	87	528
2^88+100k	88	056
2^89+100k	89	112
2^90+100k	90	224
2^91+100k	91	448
2^92+100k	92	896
2^93+100k	93	792
2^94+100k	94	584
2^95+100k	95	168
2^96+100k	96	336
2^97+100k	97	672
2^98+100k	98	344
2^99+100k	99	688
2^100+100k	0	376
2^101+100k	1	752
2^102+100k	2	504

末m位数循环

2的正幂的末m位数循环要对10^m取模，循环周期是 4·5^m-1, 始于 2^m. (具体证明涉及到数论，超出了本文的范围）

**Cycle Length for Number of Ending Digits (1 to 10)**
m	Period (4·5^m-1)	Starts with
1	4	2¹
2	20	2²
3	100	2³
4	500	2⁴
5	2500	2⁵
6	12500	2⁶
7	62500	2⁷
8	312500	2⁸
9	1562500	2⁹
10	7812500	2¹⁰

周期增长飞快-指数级增长-所以无法列出m大于3的列表。

循环的嵌套（Nesting of Cycles）

对于末m位，m-1位，m-2位， …, 末1位的循环，可以看做是嵌套的，尽管它们的起始点是交错的。你只需将较小的起始数补零，就能让它们对齐。

例如，在长度是100的末三位循环中，包含了5次长度是20的末两位循环；每一个长度是20的末两位循环包含5次长度为4的最末位循环。你从8（需移动两位）开始观察就能发现最末位的规律，末两位的规律始于08（需移动一位），末三位的规律始于008（不需移位）。

下表标出了嵌套的循环（全部100行都被标记，因为只有100个2的幂-末三位的一个循环-被列出）。

Nested 1-3 Digit Ending Patterns in Powers of Two from 2^3 to 2^102

Nested 1-3 Digit Ending Patterns From 2³ to 2¹⁰²

使用PARI/GP探索末位循环

我使用PARI/GP 来进行上面的计算和验证。下面是三个例子：

列出前20个末位是2的2的幂:

? for (i=0,19,print("2^",1+4*i,": ",2^(1+4*i)))
2^1: 2
2^5: 32
2^9: 512
2^13: 8192
2^17: 131072
2^21: 2097152
2^25: 33554432
2^29: 536870912
2^33: 8589934592
2^37: 137438953472
2^41: 2199023255552
2^45: 35184372088832
2^49: 562949953421312
2^53: 9007199254740992
2^57: 144115188075855872
2^61: 2305843009213693952
2^65: 36893488147419103232
2^69: 590295810358705651712
2^73: 9444732965739290427392
2^77: 151115727451828646838272

列出末两位的循环( ‘%’ 号返回余数，等价于取模运算):

? for (i=2,21,print("2^",i," mod(100): ",2^i % 100))
2^2 mod(100): 4
2^3 mod(100): 8
2^4 mod(100): 16
2^5 mod(100): 32
2^6 mod(100): 64
2^7 mod(100): 28
2^8 mod(100): 56
2^9 mod(100): 12
2^10 mod(100): 24
2^11 mod(100): 48
2^12 mod(100): 96
2^13 mod(100): 92
2^14 mod(100): 84
2^15 mod(100): 68
2^16 mod(100): 36
2^17 mod(100): 72
2^18 mod(100): 44
2^19 mod(100): 88
2^20 mod(100): 76
2^21 mod(100): 52

(单位的数字这里没有前补零)

打印末位1到10位数的周期长度:

? for (i=1,10,print(i,": ",4*5^(i-1)))
1: 4
2: 20
3: 100
4: 500
5: 2500
6: 12500
7: 62500
8: 312500
9: 1562500
10: 7812500

转载于:https://www.cnblogs.com/sirlipeng/p/5391096.html