A Colossal Fibonacci Numbers! (循环节)
题意:求fibonacci数列f(a^b)项mod n (0<a,b<$2^64$,$1<=n<=1000$)
题解:
我见过的fibonacci数列的常见处理方式:
1. 递推;
2. 矩阵快速幂:$$\begin{pmatrix} f(n) & f(n-1) \\ 0 & 0 \\ \end{pmatrix} * \begin{pmatrix} 1 & 1 \\ 1 & 0 \\ \end{pmatrix} = \begin{pmatrix} f(n)+f(n-1) & f(n) \\ 0 & 0 \\ \end{pmatrix} $$(这个东西老是忘记) ,定义一个矩阵类,再用快速幂运算,O(2^3*logn),ll内肯定是可以处理的,更高的连指数都要高精了;
3.fibonacci的通项:
记方程$x^2 - x - 1 = 0 $的两个根为:$$\phi = \frac{1+\sqrt{5}}{2} \ \ \hat{\phi} = \frac{1-\sqrt{5}}{2}$$ fibonacci的通项为 $$f(i) = \frac{\phi^i - \hat{\phi}^i}{\sqrt{5}}$$
证明:1.代入验证f(0)=0;f(1)=1;
2.注意到对于两个根:$$x + 1 = x^2$$ 所以:$$f(n-1)+f(n-2)\\= \frac{\phi^{i-1} - \hat{\phi}^{i-1}}{\sqrt{5}} + \frac{\phi^{i-2} - \hat{\phi}^{i-2}}{\sqrt{5}}\\=\frac{\phi^{i-1} + \phi^{i-2}}{\sqrt{5}} - \frac{\hat{\phi}^{i-1} + \hat{\phi}^{i-2}}{\sqrt{5}}\\=\frac{\phi^{i-2}(\phi+1)}{\sqrt{5}} - \frac{\hat{\phi}^{i-2}(\hat{\phi}+1)}{\sqrt{5}}\\= \frac{\phi^{i-2} \phi^2}{\sqrt{5}} - \frac{\hat{\phi}^{i-2} \hat{\phi}^{2}}{\sqrt{5}}\\= \frac{\phi^i - \hat{\phi}^i}{\sqrt{5}}\\=f(n)\\$$
同时因为$$0 \lt |\hat{\phi}| \lt 1\\0 \lt |\hat{\phi}^i| \lt 1\\\frac{| \hat{\phi}^{i}|}{\sqrt{5}} \lt \frac{1}{2}$$,所以f(i)就是$\frac{\phi^i}{sqrt{5}}$四舍五入到的整数,所以f(i)成指数增长;
可以用来证明欧几里得算法的复杂度(考虑(fi+1,fi));
4.循环节:递推公式f(n)=f(n-1)+f(n-2),所以如果有二元组(f(i),f(i-1))重复出现的话就有循环节,而在mod n 的意义下最多有n^2个不同的二元组,那么直接枚举判断就好了;
更好的求循环节(挖坑):https://blog.youkuaiyun.com/acdreamers/article/details/10983813


1 #include<cstdio> 2 #include<iostream> 3 #include<algorithm> 4 #include<cstring> 5 #include<queue> 6 #include<cmath> 7 #include<vector> 8 #include<stack> 9 #define Run(i,l,r) for(int i=l;i<=r;i++) 10 #define Don(i,l,r) for(int i=l;i>=r;i--) 11 #define ll unsigned long long 12 #define inf 0x3f3f3f3f 13 using namespace std; 14 const int N=1000010; 15 ll f[N]; 16 ll pw(ll x,ll y,ll mod){ 17 x %= mod; 18 ll res = 1; 19 for(ll i=y;i;i>>=1){ 20 if(i&1)res = res * x %mod; 21 x = x * x %mod; 22 } 23 return res; 24 } 25 int main(){ 26 //freopen("A.in","r",stdin); 27 //freopen("A.out","w",stdout); 28 int T;cin >> T; 29 ll a,b,n; 30 while(T--){ 31 cin >> a >> b >> n; 32 int i,mx=n*n+1; 33 f[0]=0;f[1]=1%n; 34 for(i=2;i<=mx;i++){ 35 f[i] = (f[i-1] + f[i-2])%n; 36 if(f[i]==f[1]&&f[i-1]==f[0]){ 37 i--; 38 break; 39 } 40 } 41 cout << f[pw(a,b,i)] << endl; 42 } 43 return 0; 44 }//by tkys_Austin;
B Choose and divide (double精度处理)
题意:求$\frac{C_p^q}{C_r^s}$的值保留5位小数(p,q,r,s<=10000)
并且答案不超过1e8;
题解:1.根据经验double一般可以保留到1e3左右的组合数;
但是题目要求1e4,可以用$C_n^m = \Pi_{i=1}^m \frac{n-i+1}{m-i+1}$这个形式一边乘一边除;
或者考虑对结果唯一分解,将1-1e4以内的质数全部找出来,利用$C_n^m = \frac{n!}{m!(n-m)!}$,这样除法就变成了对应指数的减法,看公式只需要统计N!的唯一分解就好;
2.推荐:勒让德定理:
$ L_p(n!) = \sum_{k\ge 1} [\frac{n}{p^k}] $(表示n!的唯一分解里面质因子p出现的次数)


1 #include<cstdio> 2 #include<iostream> 3 #include<algorithm> 4 #include<cstring> 5 #include<queue> 6 #include<cmath> 7 #include<vector> 8 #include<stack> 9 #define Run(i,l,r) for(int i=l;i<=r;i++) 10 #define Don(i,l,r) for(int i=l;i>=r;i--) 11 #define ll long long 12 #define inf 0x3f3f3f3f 13 using namespace std; 14 const int N=100010; 15 int p,q,r,s; 16 long double fac[N],ans1,ans2; 17 int main(){ 18 //freopen("B.in","r",stdin); 19 //freopen("B.out","w",stdout); 20 fac[0]=1; 21 for(int i=1;i<=1e4;i++)fac[i] = fac[i-1] * i; 22 while(~scanf("%d%d%d%d",&p,&q,&r,&s)){ 23 ans1=1; 24 for(int i=1;i<=max(q,s);i++){ 25 long double tmp=1; 26 if(i<=q)tmp*=1.0*(p-i+1)/(q-i+1); 27 if(i<=s)tmp/=1.0*(r-i+1)/(s-i+1); 28 ans1 *= tmp; 29 } 30 printf("%.5Lf\n",ans1); 31 } 32 return 0; 33 }//by tkys_Austin;
C GCD XOR (数学推导)
题意:求有多少对整数(a,b)满足:1<=b<=a<=n,且gcd(a,b) = a XOR b; (1<=n<=3e7)
题解:肯定不是什么算法,是数学题;
gcd(a,b) = gcd(b,a-b) ,因为a>=b>=0,所以gcd(a,b)<=a-b;
a XOR b >= a – b ;如果a的二进制每一位都不小于b的二进制每一位此时取等,否则可以互换ab的二进制某一位使得左边的结果不变而右边变大,改变后的a‘-b' <= a-b == a XOR b;
gcd(a,b)<=a-b<=a XOR b 并且gcd(a,b)=a XOR b – 》 gcd(a,b) = a XOR b = a – b;
以a为下标记录sum,枚举a-b | b ,询问O(1);


1 #include<cstdio> 2 #include<iostream> 3 #include<algorithm> 4 #include<cstring> 5 #include<queue> 6 #include<cmath> 7 #include<vector> 8 #include<stack> 9 #define Run(i,l,r) for(int i=l;i<=r;i++) 10 #define Don(i,l,r) for(int i=l;i>=r;i--) 11 #define ll long long 12 #define inf 0x3f3f3f3f 13 using namespace std; 14 const int N=30000010; 15 ll sum[N]; 16 void pre(){ 17 for(int i=1;i<N;i++){ 18 for(int j=i*2;j<N;j+=i){ 19 if((j^(j-i))==i)sum[j]++; 20 } 21 sum[i]+=sum[i-1]; 22 } 23 } 24 int main(){ 25 //freopen("C.in","r",stdin); 26 //freopen("C.out","w",stdout); 27 int T,n,Case=0; 28 scanf("%d",&T); 29 pre(); 30 while(T--){ 31 scanf("%d",&n); 32 cout << "Case "<<++Case<<": "<<sum[n]<< endl; 33 } 34 return 0; 35 }//by tkys_Austin;
D Irrelevant Elements (唯一分解定理)
题意:给出n个数,每次将相邻的两个数加起来组成长度减一的新序列,答案是最后的长度为1的序列,求最后有多少个ai和答案无关;
题解: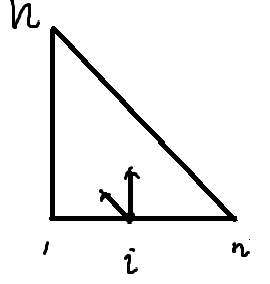
1.整个过程的结构大致是如图,横坐标表示数的个数n->1,纵坐标表示操作次数0-n-1(方便记做1-n),问题即问再最上角ai被计算了多少次;
2.观察到每一个点会贡献到其左上和正上,所以次数等于每次ai可以走左上和正上到顶点的方案数,一共有i-1次左上,n-i次正上走,且不能走出去,发现一定不会走出去,所以答案就是:C(n,i-1);
3.即处理所有的C(n,i-1)能否被p整除;
对p唯一分解为$\prod_i fac[i]^{num[i]}$,和C(n,i-1)的唯一分解比较;
$C_n^k = \frac{n-k+1}{k}C_n^{k-1}$递推所有的C(n,i-1);
组合数有关的常见公式:
$$C_n^0 = C_n^n = 1 $$
$$C_n^m = C_n^{n-m} $$
$$C_n^m = C_{n-1}^{m-1} + C_{n-1}^{m} $$
$$C_n^m = \frac{n}{n-m}C_{n-1}^m $$
$$C_n^m = \frac{n-m+1}{m}C_n^{m-1} $$
$$C_n^m = \frac{n}{m}C_{n-1}^{m-1} $$
$$\sum_{i=0}^{n} C_n^i = 2^n $$
$$\sum_{i=0}^{n} C_i^m = C_{n+1}^{m+1} $$


1 #include<cstdio> 2 #include<iostream> 3 #include<algorithm> 4 #include<cstring> 5 #include<queue> 6 #include<cmath> 7 #include<vector> 8 #include<stack> 9 #define Run(i,l,r) for(int i=l;i<=r;i++) 10 #define Don(i,l,r) for(int i=l;i>=r;i--) 11 #define ll long long 12 #define inf 0x3f3f3f3f 13 using namespace std; 14 const int N=100010,mx=100000; 15 int n,m,fac[20],sz,num[20],vis[N],pri[N],cnt; 16 vector<int>ans; 17 void pre(){ 18 for(int i=2;i<=mx;i++){ 19 if(!vis[i])pri[++cnt]=i; 20 for(int j=1;j<=cnt&&i*pri[j]<=mx;j++){ 21 vis[i*pri[j]]=1; 22 if(i%pri[j]==0)break; 23 } 24 } 25 } // 26 void init(){ 27 memset(fac,0,sizeof(fac)); 28 memset(num,0,sizeof(num)); 29 sz=0; 30 for(int i=1;i<=cnt&&m>=pri[i];i++){ 31 if(m%pri[i]==0){ 32 fac[++sz]=pri[i];num[sz]=0; 33 while(m%pri[i]==0)m/=pri[i],num[sz]++; 34 } 35 }// 36 if(m>1){fac[++sz]=m;num[sz]=1;m=1;} 37 } 38 int cal(int x,int y){int ret = 0;while(!(x%y))x/=y,ret++;return ret;} 39 bool get(int x,int y){ 40 int fg=0; 41 for(int i=1;i<=sz;i++){ 42 num[i]-=cal(x,fac[i]); 43 num[i]+=cal(y,fac[i]); 44 if(num[i]>0)fg=1; 45 } 46 return !fg; 47 } 48 int main(){ 49 pre(); 50 while(~scanf("%d%d",&n,&m)){ 51 init(); 52 ans.clear(); 53 for(int i=2;i<=n;i++){ 54 if(get(n-i+1,i-1)){ 55 ans.push_back(i); 56 } 57 } 58 printf("%d\n",(int)ans.size()); 59 for(int i=0;i<(int)ans.size();i++){ 60 if(i)printf(" "); 61 printf("%d",ans[i]); 62 } 63 puts(""); 64 } 65 return 0; 66 }//by tkys_Austin;
E Send a Table (欧拉函数)
题意:求gcd(x,y) ==1 的个数, 1<=x,y<=n , n<=5e4;
题解:
1.枚举x求$\sum \phi(i)$即可;
2.直接根据定义,枚举,求欧拉函数的和(杜教筛。。忘完了)
欧拉函数相关:
1.定义:1-n内满足gcd(i,n)==1的数的个数,$\phi(1)=1$
2.公式:
$$\phi(n) = n\prod (1-\frac{1}{pi})$$
证明1:
容斥原理可得公式:$\sum_{S \subseteq \{ p1,p2,...,pk \}} (-1)^{|S|} \frac{n}{\prod_{pi \in S} pi}$上面公式的求和每一项和这个公式的展开一一对应(展开这个括号乘积就是每个括号里面选一个);
证明2:
引理:欧拉函数是积性函数,即$\phi(nm) = \phi(n)\phi(m) \ \ \ \ gcd(n,m)=1$
证明:由孙子定理得$$\left\{ \begin{array}{} x \equiv b \pmod n \\ x \equiv c \pmod m \end{array} \right. $$ 和 $$ x \equiv c \pmod{nm} $$ 的解一一对应,同时和nm互质等价于和n,m都互质,和n,m,都互质也等价于和n,m互质,所以是积性;
p为质数 $\phi(p) = p – 1 \ \phi(p^k) = p^k - p^{k-1}$
(在p^k内只有p的倍数不会和p^k互质)
将一个数n唯一分解 $ \prod pi^{ki} $
$$ \phi(\prod pi^{ki}) = \prod \phi(pi^{ki}) $$
$$= \prod (pi^{ki} - pi^{ki-1}) $$
$$= \prod {pi^{ki}} \prod ({1 - \frac{1}{pi}} ) $$
$$= n \prod(1-\frac{1}{pi}) $$


1 #include<cstdio> 2 #include<iostream> 3 #include<algorithm> 4 #include<cstring> 5 #include<queue> 6 #include<cmath> 7 #include<vector> 8 #include<stack> 9 #define ll long long 10 #define inf 0x3f3f3f3f 11 using namespace std; 12 const int N=50010; 13 int n,fg[N],pri[N],cnt; 14 ll phi[N]; 15 void pre(){ 16 phi[1]=1; 17 for(int i=2;i<=N-10;i++){ 18 if(!fg[i])phi[pri[++cnt]=i]=i-1; 19 for(int j=1;j<=cnt&&pri[j]*i<=N-10;j++){ 20 int t=i*pri[j]; 21 fg[t]=1; 22 if(i%pri[j]==0){ 23 phi[t] = phi[i] * pri[j]; 24 break; 25 } 26 else phi[t] = phi[i] * (pri[j]-1); 27 } 28 } 29 for(int i=1;i<=N-10;i++){ 30 phi[i]+=phi[i-1]; 31 } 32 } 33 int main(){ 34 pre(); 35 while(~scanf("%d",&n)&&n){ 36 cout << (phi[n]<<1) - 1 << endl; 37 } 38 return 0; 39 }//by tkys_Austin;
F Password (编码问题)
题意:有两个6*5的矩阵,每一列出现了相同字母,那么这个字母可能是密码的那一位,求第k大的可能密码;
题解:找出每一位的可能密码,依次判断每一位放什么就好了;
G Headshot (简单概率)
题意:俄罗斯轮盘,一直一个环形的弹夹数组0无子弹,1有子弹,上一次对手已经开过枪,问这次应该转轮盘还是不要转轮盘存活的概率大;
题解:转的话活下来的概率就是选到0的概率,不转活下来就是0之后还是是0的概率;分数移项转化成整数比较;


1 #include<cstdio> 2 #include<iostream> 3 #include<algorithm> 4 #include<cstring> 5 #include<queue> 6 #include<cmath> 7 #include<vector> 8 #include<stack> 9 #define Run(i,l,r) for(int i=l;i<=r;i++) 10 #define Don(i,l,r) for(int i=l;i>=r;i--) 11 #define ll long long 12 #define inf 0x3f3f3f3f 13 using namespace std; 14 char s[10]; 15 int k,vis1[10][26],vis2[10][26],sum[10]; 16 vector<int>ans[10]; 17 int main(){ 18 int T; 19 scanf("%d",&T); 20 while(T--){ 21 scanf("%d",&k); 22 memset(vis1,0,sizeof(vis1)); 23 memset(vis2,0,sizeof(vis2)); 24 memset(sum,0,sizeof(sum)); 25 for(int i=1;i<=6;i++){ 26 scanf("%s",s+1); 27 for(int j=1;j<=5;j++)vis1[j][s[j]-'A']=1; 28 } 29 for(int i=1;i<=6;i++){ 30 scanf("%s",s+1); 31 for(int j=1;j<=5;j++)vis2[j][s[j]-'A']=1; 32 } 33 for(int i=1;i<=5;i++)ans[i].clear(); 34 sum[6]=1; 35 for(int i=5;i>=1;i--){ 36 for(int j=0;j<26;j++)if(vis1[i][j]&&vis2[i][j])ans[i].push_back(j); 37 sum[i] = sum[i+1] * ans[i].size(); 38 } 39 if(k>sum[1]){puts("NO");continue;} 40 k--; 41 for(int i=1,j;i<=5;i++){ 42 j=0;while(k>=sum[i+1])k-=sum[i+1],j++; 43 printf("%c",ans[i][j]+'A'); 44 } 45 puts(""); 46 } 47 return 0; 48 }//by tkys_Austin;
H Cows and Cars (条件概率)
题意:门后面有a头牛,b辆轿车,你会选定一个门,主持人会随机打开非你选的另一个是牛的门,问此时如果你不选开始选的门而是重新选择一个门,门后是车的概率;
题解:首先和直接选是不一样的;
分开始选的是牛和开始选的是车讨论;


1 #include<cstdio> 2 #include<iostream> 3 #include<algorithm> 4 #include<cstring> 5 #include<queue> 6 #include<cmath> 7 #include<vector> 8 #include<stack> 9 #include<iomanip> 10 #define ll long long 11 #define inf 0x3f3f3f3f 12 using namespace std; 13 int n,m,k; 14 double ans; 15 int main(){ 16 while(~scanf("%d%d%d",&m,&n,&k)){ 17 ans = 1.0*n/(n+m) * (n-1)/(n+m-k-1) + 1.0*m/(n+m) * (n)/(n+m-k-1); 18 cout << fixed << setprecision(5) << ans << endl; 19 } 20 return 0; 21 }//by tkys_Austin;
I Probability|Given (条件概率)
题意:有n个人去买东西,第i个人买东西的概率是pi,最后有r个人买了东西,问每个人实际买了东西的概率;(r<=n<=20)
题解:二进制枚举所有买东西的情况,一种状态的概率可以用乘法原理计算,全概率是所有买了r个的概率之和,用每个人在这个条件下买了东西的概率去除就好了;


1 #include<cstdio> 2 #include<iostream> 3 #include<algorithm> 4 #include<cstring> 5 #include<queue> 6 #include<cmath> 7 #include<vector> 8 #include<stack> 9 #define Run(i,l,r) for(int i=l;i<=r;i++) 10 #define Don(i,l,r) for(int i=l;i>=r;i--) 11 #define ll long long 12 #define inf 0x3f3f3f3f 13 using namespace std; 14 const int N=100; 15 int n,r,cnt[1<<21]; 16 double sum[N],tot,p[N]; 17 int main(){ 18 //freopen("I.in","r",stdin); 19 //freopen("I.out","w",stdout); 20 int Case = 0; 21 cnt[0]=0; 22 for(int i=1;i<1<<20;i++){ 23 cnt[i] = cnt[i&(i-1)] + 1; 24 } 25 while(~scanf("%d%d",&n,&r)){ 26 tot=0;for(int i=1;i<=n;i++)sum[i]=0; 27 if(!n&&!r)break; 28 for(int i=1;i<=n;i++)scanf("%lf",&p[i]); 29 for(int i=0;i<1<<n;i++)if(cnt[i]==r){ 30 double tmp = 1; 31 for(int j=1;j<=n;j++)if(i&(1<<(j-1)))tmp*=p[j];else tmp*=(1-p[j]); 32 tot += tmp; 33 for(int j=1;j<=n;j++)if(i&(1<<(j-1)))sum[j]+=tmp; 34 } 35 printf("Case %d:\n",++Case); 36 for(int i=1;i<=n;i++){ 37 printf("%.6lf\n",sum[i]/tot); 38 } 39 } 40 return 0; 41 }//by tkys_Austin;
J Double Patience (概率+状压dp,不要dfs)
题意:36张牌分成9堆,每堆4张,每次可以拿走某两堆上面点数相同的牌,求最后可以拿完的概率;
题解:$5^9 = 1953125$并不大,考虑状压dp,转移时统计出所有可以转移的概率除以转移总数,初始拿完了的概率为1;


1 #include<cstdio> 2 #include<iostream> 3 #include<algorithm> 4 #include<cstring> 5 #include<queue> 6 #include<cmath> 7 #include<vector> 8 #include<stack> 9 #define Run(i,l,r) for(int i=l;i<=r;i++) 10 #define Don(i,l,r) for(int i=l;i>=r;i--) 11 #define ll long long 12 #define inf 0x3f3f3f3f 13 using namespace std; 14 char s[10],a[10][5]; 15 int bin[10],tmp[10]; 16 double f[2000000]; 17 int main(){ 18 //freopen("J.in","r",stdin); 19 //freopen("J.out","w",stdout); 20 for(int i=bin[0]=1;i<=9;i++)bin[i] = bin[i-1] * 5; 21 while(~scanf("%s",s+1)){ 22 a[1][1]=s[1]; 23 for(int i=1;i<=9;i++) 24 for(int j=1;j<=4;j++){ 25 if(i==1&&j==1)continue; 26 scanf("%s",s+1); 27 a[i][j] = s[1]; 28 } 29 memset(f,0,sizeof(f)); 30 f[0]=1; 31 for(int i=1;i<bin[9];i++){ 32 int v=i;for(int j=1;j<=9;j++,v/=5)tmp[j]=v%5; 33 int cnt = 0; 34 for(int j=1;j<=9;j++) 35 for(int k=j+1;k<=9;k++)if(i!=j&&tmp[j]&&tmp[k]&&a[j][tmp[j]]==a[k][tmp[k]]){ 36 cnt++; 37 f[i] += f[i - bin[j-1] - bin[k-1]]; 38 } 39 if(!cnt)continue; 40 f[i] /= cnt; 41 } 42 printf("%.6lf\n",f[bin[9]-1]); 43 } 44 return 0; 45 }//by tkys_Austin;
在写递推的题之前先打个补丁OVO:
Catalan数及其应用:
1.定义:
递推式 $h(0)=h(1)=1 \\ h(n) = h(0)h(n-1) + h(1)(n-2) + h(2)h(n-3) + ... + h(n-1)h(0)$
另类递推式 $h(n) = \frac{4n-2}{n+1}h(n-1)$
递推式的解 $h(n) = \frac{C_{2n}^{n}}{n+1}$
另类递推式的解 $h(n) = C_{2n}^{n} - C_{2n}^{n-1}$
、
2.应用:https://www.cnblogs.com/yaoyueduzhen/p/5456490.html(这篇比较好)
①出栈序列,括号序列 (对应h(h)的Catalan递推式,同时可以用来推导出另类递推式的解)
②二叉树形态(对应h(n)的Catalan递推式)
③多边形的三角剖分(对应h(n-2)的catalan递推式)
④n*n的格子只能走下三角的问题(对应括号序列)
⑤圆上2n个点的n条不相交线段(对应括号序列)
(比较常用的应该这些)
其前几项为 : 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440,…
(下标从0)
K Critical Mass (容斥或dp或递推)
题意:一个长度为n只有U和L的排列,求有多少种方案使得有三个U相邻(n<=30);
还是用lrj的方法吧:
$f(n)$为前n个位置有三个U连在一起的方案,同时$g(n) = 2^n – f(n)$
枚举第一个连续三个U的位置i,i,i+1,i+2位置都为U,同时i-1必须不为U(因为i第一个出现),i+3到n任选,特殊考虑没有i-1的1号位置;
所以:$f(n) = 2^{n-3} + \sum_{i=2}^{n-2}g(i-2)2^{n-i-2} $


1 #include<cstdio> 2 #include<iostream> 3 #include<algorithm> 4 #include<cstring> 5 #include<queue> 6 #include<cmath> 7 #include<vector> 8 #include<stack> 9 #define Run(i,l,r) for(int i=l;i<=r;i++) 10 #define Don(i,l,r) for(int i=l;i>=r;i--) 11 #define ll long long 12 #define inf 0x3f3f3f3f 13 using namespace std; 14 const int N=100; 15 int n; 16 ll f[N]; 17 int main(){ 18 f[0]=f[1]=f[2]=0; f[3]=1; 19 for(int i=4;i<=30;i++){ 20 f[i] = (i-1) * (1ll<<(i-4)); 21 for(int j=2;j<=i-2;j++){ 22 f[i] -= f[j-2] * (1<<(i-j-2)); 23 } 24 } 25 while(~scanf("%d",&n)&&n){ 26 cout << f[n] << endl; 27 } 28 return 0; 29 }//by tkys_Austin;
L Pole Arrangement (方案dp)
题意:有n根高度互不相同的竹竿,求有多少种排列方式,使得从左可以看到l根,从右可以看到j根;(1<=l,r<=n<=20)
solve 1:
d(i,j,k)表示i根竹竿,左右分别看到j,k,的方案数;考虑最矮的那根竹竿,分放在最左边,最右边,和中间讨论:
$d(i,j,k) = d(i-1,j-1,k) + d(i-1,j,k-1) + (i-2) * d(i-1,j,k)$
solve 2:
有一种O(n^2)的方法;
枚举最高的位置,最高的位置在被看到的同时一定会阻挡左右两边的视线,所以可以分别考虑左右两边,假设f(i,j)表示i根竹竿从左看去有j根的方案数,答案是:$\sum_{i=1}^{n}C_{n-1}^{i-1}f(i-1,l-1)f(n-i,r-1)$,
参考sol1的方式递推f,$f(i,j) = f(i-1,j-1) + (i-1)f(i-1,j)$
solve2没试过(因为我果断抄袭了lrj的做法),有问题的话欢迎各路神犇指出……


1 #include<cstdio> 2 #include<iostream> 3 #include<algorithm> 4 #include<cstring> 5 #include<queue> 6 #include<cmath> 7 #include<vector> 8 #include<stack> 9 #define Run(i,l,r) for(int i=l;i<=r;i++) 10 #define Don(i,l,r) for(int i=l;i>=r;i--) 11 #define ll long long 12 #define inf 0x3f3f3f3f 13 using namespace std; 14 const int N=110; 15 ll f[N][N][N]; 16 int main(){ 17 f[1][1][1]=1; 18 for(int i=2;i<=20;i++) 19 for(int j=1;j<=i;j++) 20 for(int k=1;k<=i;k++){ 21 f[i][j][k] = f[i-1][j-1][k] + f[i-1][j][k-1] + f[i-1][j][k] * (i-2); 22 } 23 int T,n,l,r;scanf("%d",&T); 24 while(T--){ 25 scanf("%d%d%d",&n,&l,&r); 26 cout << f[n][l][r] << endl; 27 } 28 return 0; 29 }//by tkys_Austin;
M Crossing Rivers (期望)
英语题;
题意:家在A,在最左边,公司在B,在最右边 ,AB距离D,中间有许多河,长度为L,河上有船,船速为v,当你到一条河的河岸时,船以相等的概率可能在任意位置,求A到B的期望时间;
题解:陆地时间确定,每条河的期望时间((3L+L)/v) = (2L/v) ans = D-sum(L) + sum(2L/v)


1 #include<cstdio> 2 #include<iostream> 3 #include<algorithm> 4 #include<cstring> 5 #include<queue> 6 #include<cmath> 7 #include<vector> 8 #include<stack> 9 #define Run(i,l,r) for(int i=l;i<=r;i++) 10 #define Don(i,l,r) for(int i=l;i>=r;i--) 11 #define ll long long 12 #define inf 0x3f3f3f3f 13 using namespace std; 14 int n,D,L[20],p[20],v[20]; 15 double ans; 16 int Case; 17 int main(){ 18 //freopen("L.in","r",stdin); 19 //freopen("L.out","w",stdout); 20 while(~scanf("%d%d",&n,&D)){ 21 if(!n&&!D)break; 22 Run(i,1,n)scanf("%d%d%d",&p[i],&L[i],&v[i]); 23 ans = D; 24 for(int i=1;i<=n;i++){ 25 ans -= L[i]; 26 ans += L[i]*2.0/v[i]; 27 } 28 printf("Case %d: %.3lf\n\n",++Case,ans); 29 } 30 return 0; 31 }//by tkys_Austin;
N Coupons (期望dp-》递推公式)
题意:每次购买彩票随机获得一种图案,图案共n种,买一次彩票会随机得到一种图案,求得到n种图案的期望购买次数(n<=33)
题解:
一个比较经典的模型;
注意到如果手上已经有m种,那么再买一次买重复的概率$\frac{m}{n}$,买到新的的概率$\frac{n-m}{n}$;
令$f_i$为现在已经集齐了i种还需要的期望次数($f_n = 0$,$ans = f_0$),由上面说的再买一次得到 $f_i = \frac{i}{n}f_{i} + \frac{n-i}{n}f_{i+1} + 1$化简得 $f_i = f_{i+1} + \frac{n}{n-i}$ ,其实和dp没什么关系$ans = f_0 = n\sum_{i=1}^{n} \frac{1}{i}$


1 #include<cstdio> 2 #include<iostream> 3 #include<algorithm> 4 #include<cstring> 5 #include<queue> 6 #include<cmath> 7 #include<vector> 8 #include<stack> 9 #define Run(i,l,r) for(int i=l;i<=r;i++) 10 #define Don(i,l,r) for(int i=l;i>=r;i--) 11 #define ll long long 12 #define inf 0x3f3f3f3f 13 using namespace std; 14 const int N=50; 15 int n; 16 ll gcd(ll a,ll b){return(!b)?a:gcd(b,a%b);} 17 struct Fra{ 18 ll a,b; 19 Fra(ll A=0,ll B=1){ 20 ll g=gcd(B,A); 21 if(g)A/=g,B/=g; 22 a=A;b=B; 23 }; 24 Fra operator +(const Fra&A){return Fra(a*A.b+A.a*b,b*A.b);} 25 Fra operator *(const Fra&A){return Fra(a*A.a,b*A.b);} 26 void print(){ 27 if(!(a%b)){ 28 printf("%lld\n",a/b); 29 return; 30 } 31 ll tmp=a/b,cnt1=0; 32 while(tmp)cnt1++,tmp/=10; 33 for(int i=1;i<=cnt1+1;i++)printf(" "); 34 printf("%lld\n",a%b); 35 printf("%lld ",a/b); 36 tmp=b;int cnt2=0; 37 while(tmp)cnt2++,tmp/=10; 38 for(int i=1;i<=cnt2;i++)printf("-"); 39 printf("\n"); 40 for(int i=1;i<=cnt1+1;i++)printf(" "); 41 printf("%lld\n",b); 42 } 43 }f[N]; 44 int main(){ 45 //freopen("N.in","r",stdin); 46 //freopen("N.out","w",stdout); 47 for(int i=1;i<=33;i++){ 48 f[i] = f[i-1] + Fra(1,i); 49 } 50 while(~scanf("%d",&n)){ 51 Fra ans = f[n] * Fra(n,1); 52 ans.print(); 53 } 54 return 0; 55 }//by tkys_Austin;
O Probability (积分)
补点文化课,提前规划退役生活。。。。
导数的概念:
$f'(x) = \lim_{ \Delta x \to 0} \frac{\Delta y }{\Delta x}\\
= \lim_{ \Delta x \to 0} \frac{f(x_2) - f(x_1)}{\Delta x}\\
= \lim_{ \Delta x \to 0} \frac{f(x+\Delta x) - f(x)}{\Delta x}$
基本初等函数的导数公式:
$f(x) = c , f'(x) = 0 \\
f(x) = x^{\alpha} , f'(x) = \alpha x^{\alpha-1} \\
f(x) = sin x , f'(x) = cos(x) \\
f(x) = cos x , f'(x) = -sin(x) \\
f(x) = a^x , f'(x) = a^{x}ln(a) \\
f(x) = e^x , f'(x) = e^{x} \\
f(x) = log_{a}x , f'(x) = \frac{1}{xlna} \\
f(x) = ln x , f'(x) = \frac{1}{x}$
导数运算法则 :
$[f(x)\pm g(x)]'=f'(x)\pm g'(x)$
$[cf(x)]' = cf'(x) $
$[f(x) \cdot g(x)]' = f'(x)g(x) + f(x)g'(x) $
$[ \frac{ 1 }{ g(x) } ]' = - \frac{ g'(x) }{ g^2(x) }$
$[\frac{f(x)}{g(x)}]' = \frac{f'(x)g(x) - f(x)g'(x)}{g^2(x)} $
复合函数的求导法则:
对于$y = f(g(x))$我们令:$y = f(u) , u = g(x) ;$
则:$y_{x}' = y_{u}' \cdot u_{x}'$
函数的单调性和与极值(略):
只是注意导数正负的意义同时最大最小的判定区别就好;
定积分的概念:
如果函数$f(x)$在区间$[a,b]$内连续,用点$a = x_0 < x_1 < x_2 < \cdots < x_{i-1} < x_{i} < \cdots < x_{n} = b $将区间$[a,b]$等分为n个小区间,在每个小区间$[x_{i-1},x_{i}]$上任取一点$\xi_{i}(i=1,2,\cdots,n) $,做和式,当$n \to \infty$时,和式无限趋近于某个常数,叫做函数$f(x)$在$[a,b]$上的定积分:$$\int_{a}^{b}f(x)dx = \lim_{n \to \infty} \sum_{i=1}^{n} \frac{b-a}{n}f(\xi_{i})$$
实际的计算里面,我们常令:$\xi_{i} = \frac{b-a}{n}*(i-1) + a$
定积分的性质:
$\int_{a}^{b}kf(x)dx = k \int_{a}^{b}f(x)dx\\
\int_{a}^{b}[f_1(x) \pm f_2(x)]dx = \int_{a}^{b}f_1(x)dx \pm \int_{a}^{b}f_2(x)dx \\
\int_{a}^{b}f(x)dx = \int_{a}^{c}f(x)dx + \int_{c}^{b}f(x)dx (a<c<b)$
微积分基本定理:(牛顿-莱布尼茨公式)
一般地,如果$$是区间$$上的连续函数,并且,那么$\int_{a}^{b}f(x)dx = F(x)|_{a}^{b} = F(b) - F(a)$;
常用定积分公式:
$\int_{a}^{b}c dx = cx|_{a}^{b} \\
\int_{a}^{b}x^n dx = \frac{1}{n+1}x^{n+1}|_{a}^{b}\\
\int_{a}^{b}cosx dx = sinx|_{a}^{b}\\
\int_{a}^{b}sinx dx = -cosx|_{a}^{b}\\
\int_{a}^{b}\frac{1}{x} dx = lnx|_{a}^{b}\\
\int_{a}^{b}e^x dx = e^x|_{a}^{b}\\
\int_{a}^{b}a^x dx = \frac{a^x}{lna}|_{a}^{b}$
题意:在[-a,b]*[-b,b]的区域内随机选择一个点P,求以(0,0)和P为对角线的长方形面积大于S的概率(a,b>0,S>=0)
题解:
只管第第一象限就好了,第一象限满足面积==s的点实际上就是反比例函数y = S/x , 之后反比例函数会和[0,0][a,b]形成的矩形有交,交的外侧区域就是我们想要的面积,用它去除[0,0][a,b]的面就好了;
现在来管面积,先去求内部的面积,分成一个矩形和反比例函数和x围成的区域求,由定积分的定义分即
$\frac{S}{b} \cdot b + \int_{\frac{S}{b}}^{a} \frac{S}{x} dx \\
= S + S \cdot lnx|_{\frac{S}{b}}^{a} \\
= S + S \cdot (ln(a) - ln(\frac{S}{b}) ) \\
= S + S \cdot ln(\frac{ab}{S}) \\$
可以根据这个减减除除得到答案;


1 #include<cstdio> 2 #include<iostream> 3 #include<algorithm> 4 #include<cstring> 5 #include<queue> 6 #include<cmath> 7 #include<vector> 8 #include<stack> 9 #define Run(i,l,r) for(int i=l;i<=r;i++) 10 #define Don(i,l,r) for(int i=l;i>=r;i--) 11 #define ll long long 12 #define inf 0x3f3f3f3f 13 using namespace std; 14 double S,a,b; 15 const double eps = 1e-18; 16 int main(){ 17 int N;scanf("%d",&N); 18 while(N--){ 19 scanf("%lf%lf%lf",&a,&b,&S); 20 if(fabs(S)<eps)puts("100.000000%"); 21 else if(a*b-S<eps)puts("0.000000%"); 22 else printf("%.6lf%%\n",(a*b-S-S*(log(a*b/S)))/(a*b)*100); 23 } 24 return 0; 25 }//by tkys_Austin;
P So you want to be a 2n-aire? (期望最优和概率相关)
题意:一开始有1块钱,最多有n次答题,答对奖金翻倍,答错奖金清零,一直答对的概率为[t,1]内随机分布的数,每次你可以选择继续答题或者直接拿走奖金,求在最优的策略下,奖金的期望值;
题解:
大概是里面最难理解的一个题了吧;
开始我是这样子认为的:设d[i]为答对第i题的最优奖金期望,既然概率是[t,1]内随机分布的,我们看成(t+1)/2就好了,那还dp什么呢,直接就看(t+1)/2和2的大小就好了啊;
确实是有问题的;过河的那个题可以去中间值,但是本题不行,因为本题p(假设的一个已经确定的[t,1]内的数表示概率)是会影响d[i]的决策的;
d[i] = max(d[i+1] * p , 2^i); 当p<(2^i/d[i+1])和p>(2^i/d[i+1])是不同的;
分别考虑两种的期望再求和才对;


1 #include<cstdio> 2 #include<iostream> 3 #include<algorithm> 4 #include<cstring> 5 #include<queue> 6 #include<cmath> 7 #include<vector> 8 #include<stack> 9 #define Run(i,l,r) for(int i=l;i<=r;i++) 10 #define Don(i,l,r) for(int i=l;i>=r;i--) 11 #define ll long long 12 #define inf 0x3f3f3f3f 13 using namespace std; 14 const int N=31; 15 double d[N]; 16 int n; 17 double p,p0,p1; 18 int main(){ 19 while(~scanf("%d%lf",&n,&p)){ 20 if(n==0&&fabs(p)<1e-18)break; 21 memset(d,0,sizeof(d)); 22 d[n] = 1<<n; 23 for(int i=n-1;~i;i--){ 24 p0 = max(p,1.0 * (1<<i) / d[i+1]); 25 p1 = (p0-p) / (1-p); 26 d[i] = p1 * (1<<i) + (1-p1) * (1+p0)/2 * d[i+1]; 27 } 28 printf("%.3lf\n",d[0]); 29 } 30 return 0; 31 }//by tkys_Austin;
Q Polygon (概率小游戏)
题意:有一根长度为n的木条,随机选k个位置把它们切成k+1段,求这些木条可以形成一个多边形的概率;
题意:
可以切成小数长度,和n并没有什么关系;
可以形成多边形的条件是任意一边都小于(n/2),或者说1-有一边大于(n/2)的概率(因为不会有两边大于(n/2),这里取不取等对概率计算没什么关系),在木条上选k个点等价于在圆周上选取k+1个点,考虑两个点之间间距大于半圆,枚举这两个点顺时针的第一个点,另外的所有k个点一定全分布在这个点逆时针往后(n/2)之后的(n/2)部分;
由乘法原理得答案是:1 – (k + 1) / (1/2)^k


1 #include<cstdio> 2 #include<iostream> 3 #include<algorithm> 4 #include<cstring> 5 #include<queue> 6 #include<cmath> 7 #include<vector> 8 #include<stack> 9 #define Run(i,l,r) for(int i=l;i<=r;i++) 10 #define Don(i,l,r) for(int i=l;i>=r;i--) 11 #define ll long long 12 #define inf 0x3f3f3f3f 13 using namespace std; 14 int n,k; 15 ll gcd(ll a,ll b){return !b?a:gcd(b,a%b);} 16 int main(){ 17 int T;scanf("%d",&T); 18 int Case = 0; 19 while(T--){ 20 scanf("%d%d",&n,&k); 21 ll a = (1ll<<k) - k - 1; 22 ll b = (1ll<<k); 23 if(!a)b=1; 24 else { 25 ll g = gcd(a,b); 26 a /= g; 27 b /= g; 28 } 29 cout << "Case #" << ++Case << ": " << a << "/" << b << endl; 30 } 31 return 0; 32 }//by tkys_Austin;
R The Counting Problem (数位dp)
题意:[a,b]之间有每个数字出现了多少次;
题解:
感觉我的做法有点麻烦,一个不太数位的数位dp
g[i][0/1][0/1]表示dp到第i为是否满足数位限制,是否有前导零的方案数;
根据g转移的时候会枚举当前位的数字,这个时候顺便统计答案;


1 #include<cstdio> 2 #include<iostream> 3 #include<algorithm> 4 #include<cstring> 5 #include<queue> 6 #include<cmath> 7 #include<vector> 8 #include<stack> 9 #define Run(i,l,r) for(int i=l;i<=r;i++) 10 #define Don(i,l,r) for(int i=l;i>=r;i--) 11 #define ll long long 12 #define inf 0x3f3f3f3f 13 using namespace std; 14 const int N=50; 15 int bin[N],l,r,tmp[N],cnt,sum1[N],sum2[N],num[N],g[N][2][2]; 16 void dp(){ 17 memset(g,0,sizeof(g)); 18 memset(sum1,0,sizeof(sum1)); 19 g[cnt+1][1][1]=1; 20 for(int i=cnt+1;i>1;i--) 21 for(int lim=0;lim<2;lim++) 22 for(int fg=0;fg<2;fg++){ 23 int R = lim ? tmp[i-1] : 9; 24 for(int j=0;j<=R;j++){ 25 g[i-1][lim&&j==tmp[i-1]][fg&&!j]+=g[i][lim][fg]; 26 if(fg&&!j)continue; 27 sum1[j] += g[i][lim][fg] * (lim&&j==tmp[i-1]?(num[i-2]+1):bin[i-2]); 28 } 29 } 30 sum1[0]++; 31 }// 32 int main(){ 33 //freopen("R.in","r",stdin); 34 //freopen("R.out","w",stdout); 35 for(int i=bin[0]=1;i<=9;i++)bin[i] = bin[i-1] * 10; 36 while(~scanf("%d%d",&l,&r)){ 37 if(!l&&!r)break; 38 if(l>r)swap(l,r); 39 cnt=0;l--; 40 while(l)tmp[++cnt]=l%10,l/=10,num[cnt]=num[cnt-1]+tmp[cnt]*bin[cnt-1]; 41 dp(); 42 for(int i=0;i<10;i++)sum2[i]=sum1[i]; 43 cnt=0; 44 while(r)tmp[++cnt]=r%10,r/=10,num[cnt]=num[cnt-1]+tmp[cnt]*bin[cnt-1]; 45 dp(); 46 for(int i=0;i<9;i++){ 47 cout << sum1[i] - sum2[i] <<" "; 48 } 49 cout << sum1[9] - sum2[9] <<endl; 50 } 51 return 0; 52 }//by tkys_Austin;
S How Many Pieces of Land ? (递推,求和+高精度)
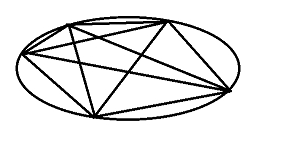
题意:一个椭圆形的土地,在土地边缘上选n个点,n个点构成完全图,线和线之间相交会形成新的点,问将可以将土地分成的最大块数;
题解:
低次方和公式:
$\sum_{i=1}^{n} = \frac{n(n+1)}{2}\\
\sum_{i=1}^{n} = \frac{n(n+1)(2n+1)}{6}\\
\sum_{i=1}^{n} = \frac{n^2(n+1)^2}{4} \\
$
提供两种推导:
第一种化简多点,第二种想法多点;但都要用到欧拉公式: V-E+F = 2 (点-边+面=2);最多的时候是没有任何三线在土地内部共点,统计此时的点数和边数,注意这里的E要包括外面的圆弧,算出的V是包括了最外面的一个面的;
①点:内部点是由两条线段相交而成,枚举第一条直线,再考虑直线左右两边在边缘上的点可以任意形成直线和枚举的直线相交成点,每个点会被统计四次 所以除以4,加上在边缘上的点;
边:同样枚举第一条直线,数在这条直线上的边,在这条直线上点数为边数+1,每条边会被枚举两次所以除以二,加上最外面的n条线和n条圆弧;
$$V = n + n \cdot \frac{\sum_{i=1}^{n-3} i\cdot(n - 2 - i)}{4} \\
E = n + n + n \cdot \frac{\sum_{i=1}^{n-3} (i \cdot (n-2-i) + 1) }{2} $$
$$E - V + 2 - 1\\= n + \frac{n}{4}\sum_{i=1}^{n-3}(i(n-2-i)+2) + 1 \\
= \frac{n}{24}(n^3-6n^2+23n-18)+1 $$
②点:任选四个边缘上的点(C(n,4))对应一个内部点,加上边缘的n个;
边:一个点必和四条边相邻,将内部点数*4,此时给有一个端点时边缘点的线段加上一次,两个点都是边缘点的线段加上两次(你会发现需要补的数目就是2C(n,2)),这样每条边都算了两次(左右端点各一次),总数除以4再加上弦的个数;
$$V = C_{n}^{4} + n\\E = \frac{4C_{n}^{4} + 2C_{n}^{2}}{2}\\E - V + 1\\= C_{n}^{4} + C_{n}^{2} + 1$$
化出来也是一样的;
https://en.wikipedia.org/wiki/Dividing_a_circle_into_areas#Lemma


1 #include<cstdio> 2 #include<iostream> 3 #include<algorithm> 4 #include<cstring> 5 #include<queue> 6 #include<cmath> 7 #include<vector> 8 #include<stack> 9 #define Run(i,l,r) for(int i=l;i<=r;i++) 10 #define Don(i,l,r) for(int i=l;i>=r;i--) 11 #define ll long long 12 #define inf 0x3f3f3f3f 13 using namespace std; 14 const int base = 10000,N=100; 15 int n; 16 struct Bign{ 17 int len,c[N]; 18 Bign(){memset(c,0,sizeof(c));len=0;} 19 void zero(){ 20 while(len&&!c[len])len--; 21 } 22 void write(char *s){ 23 memset(c,0,sizeof(c)); 24 c[len=0]=0; 25 int l = strlen(s); 26 for(int i=l-1,k=1;~i;i--,k*=10){ 27 if(k==base)k=1,len++; 28 c[len]+=(s[i]-'0')*k; 29 } 30 } 31 void read(){ 32 char s[N*4]; 33 scanf("%s",s); 34 write(s); 35 } 36 void print(){ 37 // zero(); 38 printf("%d",c[len]); 39 Don(i,len-1,0)printf("%04d",c[i]); 40 printf("\n"); 41 } 42 Bign operator =(const int&A){ 43 char s[20]; 44 sprintf(s,"%d",A); 45 write(s); 46 return *this; 47 } 48 Bign operator +(const Bign&A){ 49 Bign ret; 50 ret.len = max(len,A.len)+2; 51 Run(i,0,len){ 52 ret.c[i] += c[i] + A.c[i]; 53 if(ret.c[i]>=base)ret.c[i]-=base,ret.c[i+1]++; 54 } 55 ret.zero(); 56 return ret; 57 } 58 Bign operator +(const int&A){ 59 Bign tmp; 60 tmp = A; 61 return *this + tmp; 62 } 63 Bign operator -(const Bign&A){ 64 Bign ret; 65 ret.len = len; 66 Run(i,0,len){ 67 ret.c[i] += c[i] - A.c[i]; 68 if(ret.c[i]<0)ret.c[i]+=base,ret.c[i+1]--; 69 } 70 ret.zero(); 71 return ret; 72 } 73 Bign operator -(const int&A){ 74 Bign tmp; 75 tmp = A; 76 return *this - tmp; 77 } 78 Bign operator *(const Bign&A){ 79 Bign ret; 80 ret.len = len + A.len + 2; 81 Run(i,0,len) 82 Run(j,0,A.len){ 83 ret.c[i+j] += c[i] * A.c[j]; 84 if(ret.c[i+j]>=base){ 85 ret.c[i+j+1] += ret.c[i+j]/base; 86 ret.c[i+j] %= base; 87 } 88 } 89 Run(i,0,ret.len){ 90 if(ret.c[i]>=base){ 91 ret.c[i+1] += ret.c[i]/base; 92 ret.c[i] %= base; 93 } 94 } 95 ret.zero(); 96 return ret; 97 } 98 Bign operator *(const int&A){ 99 Bign tmp; 100 tmp = A; 101 return *this * tmp; 102 } 103 bool operator <(const Bign&A)const{ 104 if(len!=A.len)return len < A.len; 105 Don(i,len,0){ 106 if(c[i]!=A.c[i])return c[i] < A.c[i]; 107 } 108 return false; 109 } 110 Bign operator /(const Bign&A){ 111 Bign ret,r,a; 112 a = A; 113 ret.len = len; 114 for(int i=len;~i;i--){ 115 r = r * base + c[i]; 116 int L = 0,R = base,div; 117 Bign tmp; 118 while(L<=R){ 119 int mid = (L + R) >> 1; 120 tmp = a * mid; 121 if(r < tmp) R = mid - 1; 122 else div = mid , L = mid + 1; 123 } 124 ret.c[i] = div; 125 r = r - a * div; 126 } 127 ret.zero(); 128 return ret; 129 } 130 Bign operator /(const int&A){ 131 Bign tmp; 132 tmp = A; 133 return *this / tmp; 134 } 135 }; 136 int main(){ 137 //freopen("S.in","r",stdin); 138 //freopen("S.out","w",stdout); 139 int T;scanf("%d",&T); 140 while(T--){ 141 scanf("%d",&n); 142 Bign ans,tmp; 143 ans=1;tmp=1; 144 if(n<=3)ans=0; 145 else ans = ans * n * (n-1) * (n-2) * (n-3) / 24; 146 tmp = tmp * n * (n-1) / 2 + 1; 147 ans = ans + tmp; 148 ans.print(); 149 } 150 return 0; 151 }//by tkys_Austin;
T ASCII Area (计算几何)
题意:一个ASCLL图案组成的多边形,\,/表示边界,求多边形面积;
题解:内部点+边缘点数/2即可,一个点在多变形内部当它前面有奇数个边界;


1 #include<cstdio> 2 #include<iostream> 3 #include<algorithm> 4 #include<cstring> 5 #include<queue> 6 #include<cmath> 7 #include<vector> 8 #include<stack> 9 #define Run(i,l,r) for(int i=l;i<=r;i++) 10 #define Don(i,l,r) for(int i=l;i>=r;i--) 11 #define ll long long 12 #define inf 0x3f3f3f3f 13 using namespace std; 14 const int N=110; 15 int n,m,cnt,sum; 16 char s[N]; 17 int main(){ 18 //freopen("S.in","r",stdin); 19 //freopen("S.out","w",stdout); 20 while(~scanf("%d%d",&n,&m)){ 21 sum=0; 22 for(int i=1;i<=n;i++){ 23 scanf("%s",s+1); 24 cnt=0; 25 for(int j=1;j<=m;j++){ 26 if(s[j]=='.')sum+=(cnt&1)<<1; 27 else sum++,cnt++; 28 } 29 } 30 printf("%d\n",sum>>1); 31 } 32 return 0; 33 }//by tkys_Austin;
U Joseph's Problem (下底分块)
题意:计算$\sum_{i=1}^{n} k \ mod \ i (1 \le n,k, \le 10^9)$
题解:
模数是变化的,运算律失效了,但是取余等于原数 – [原数/模数]*模数;
统计k的和,统计[k/i]*i的和,相减;
下底分块:
1.$\lfloor n/i \rfloor (i=1,\cdots,n)$的取值不同个数为$O(\sqrt{n})$
证明:1到根号n最大每个不同,根号n到n的取值在1到根号n之间,所以最多也是根号n个;
2.$\lfloor \frac{n}{\lfloor \frac{n}{i} \rfloor }\rfloor$的意义是使得$\lfloor \frac{n}{j} \rfloor = \lfloor \frac{n}{i} \rfloor $成立的最大的j;
证明:
设$ n = qi + r (r \lt i)$,那么$\lfloor \frac{n}{i} \rfloor = q $,
先证明$\lfloor \frac{n}{q} \rfloor $是可以的;
$$LHS = \lfloor \frac{n}{\lfloor \frac{n}{q} \rfloor}\rfloor= \lfloor \frac{qi + r}{\lfloor i + \frac{r}{q} \rfloor} \rfloor$$
再设$r = vq + w (w \lt q)$,观察到:$w \lt q \ , \ w \le r \lt i \lt (i+v)$
$$LHS = \lfloor \frac{q(i+v) + w}{\lfloor (i+v) + \frac{w}{q} \rfloor } \rfloor = \lfloor \frac{q(i+v) + w}{i+v} \rfloor = q$$
再证明$\lfloor \frac{n}{q} \rfloor + 1$不行;
另设:$p = \lfloor \frac{n}{q} \rfloor$
由取下整的定义易知:
$$\frac{n}{q}-1 \lt p \le \frac{n}{q}\\ \frac{n}{q} \lt p + 1\\ \lfloor \frac{n}{p+1} \rfloor \le \frac{n}{p+1} \lt q $$
结合下整符号的单调性撕烤一下整个证明就完工了;
所以可以根据2往后跳,1保证了$O(\sqrt{n})$的复杂度;
回到这个题,套用这个方法就可以了(恶心的是证明,大可跳过这些无聊的证明)


1 #include<cstdio> 2 #include<iostream> 3 #include<algorithm> 4 #include<cstring> 5 #include<queue> 6 #include<cmath> 7 #include<vector> 8 #include<stack> 9 #define Run(i,l,r) for(int i=l;i<=r;i++) 10 #define Don(i,l,r) for(int i=l;i>=r;i--) 11 #define ll long long 12 #define inf 0x3f3f3f3f 13 using namespace std; 14 ll ans=0; 15 int n,k; 16 int main(){ 17 while(~scanf("%d%d",&n,&k)){ 18 ans = 1ll * n * k; 19 n = min(n,k); 20 for(int i=1,last;i<=n;i=last+1){ 21 last = min(k/(k/i),n); 22 ans -= 1ll * (k/i) * (i+last) * (last-i+1) / 2; 23 } 24 cout << ans << endl; 25 } 26 return 0; 27 }//by tkys_Austin;
V Help Tomisu (n!欧拉函数递推 )
题意:给出N,M统计1-N!之间有多少个整数x满足:x的所有素因子都大于M,($2 \le N \le 10^7 , 1 \le M \le N , N – M \le 10^5$)
题解:
条件等价于和M!互质,对于k>M!取模就好了;
现在我们只需要判断1-M!里面和n互质的数的个数即$\phi(M!)$
根据计算式递推即可;


1 #include<cstdio> 2 #include<iostream> 3 #include<algorithm> 4 #include<cstring> 5 #include<queue> 6 #include<cmath> 7 #include<vector> 8 #include<stack> 9 #include<map> 10 #define Run(i,l,r) for(int i=l;i<=r;i++) 11 #define Don(i,l,r) for(int i=l;i>=r;i--) 12 #define ll long long 13 #define inf 0x3f3f3f3f 14 using namespace std; 15 const int N=1e7+1,mod = 100000007; 16 int n,m,vis[N],pri[N],cnt,phi[N]; 17 void pre(){ 18 phi[1]=1; 19 for(int i=2;i<N;i++){ 20 if(!vis[i])phi[pri[++cnt]=i] = 1ll * phi[i-1] * (i-1) %mod; 21 else phi[i] = 1ll * phi[i-1] * i %mod; 22 int t; 23 for(int j=1;j<=cnt&&i*pri[j]<N;j++){ 24 t = i * pri[j]; 25 vis[t] = 1; 26 if(i % pri[j]==0) break; 27 } 28 } 29 } 30 int main(){ 31 //freopen("V.in","r",stdin); 32 //freopen("V.out","w",stdout); 33 pre(); 34 while(~scanf("%d%d",&n,&m)){ 35 if(!n&&!m)break; 36 ll ans = phi[m]; 37 for(int i=m+1;i<=n;i++)ans = 1ll * ans * i %mod; 38 printf("%lld\n",(ans-1+mod)%mod); 39 } 40 return 0; 41 }//by tkys_Austin;
W trees in a Wood. (mobius/欧拉函数+枚举)
题意:$|x| \le a , |y| \le b (a \le 2000 , b \le 2000000)$的网格中,除了原点以外种了可爱的树,树可以相互遮挡,问从原点可以看到多少树;
题解:
坐标轴上一共看得到四颗,剩下的四个象限对称;
当且仅当(x,y)互质时看得到;
发现a很小,枚举,参考上一题gcd有循环节,求出phi(x) , 最后的剩下的那小段单独处理;


1 #include<cstdio> 2 #include<iostream> 3 #include<algorithm> 4 #include<cstring> 5 #include<queue> 6 #include<cmath> 7 #include<vector> 8 #include<stack> 9 #include<map> 10 #define Run(i,l,r) for(int i=l;i<=r;i++) 11 #define Don(i,l,r) for(int i=l;i>=r;i--) 12 #define ll long long 13 #define inf 0x3f3f3f3f 14 using namespace std; 15 const int N=2010; 16 int n,m,sum[N][N]; 17 int gcd(int x,int y){return (!y)?x:gcd(y,x%y);} 18 void pre(){ 19 for(int i=1;i<=2000;i++) 20 for(int j=1;j<=2000;j++){ 21 if(gcd(i,j)==1)sum[i][j] = 1; 22 sum[i][j] += sum[i][j-1]; 23 } 24 } 25 int main(){ 26 pre(); 27 while(~scanf("%d%d",&n,&m)){ 28 if(!n&&!m)break; 29 ll ans = 0; 30 for(int i=1;i<=n;i++){ 31 ans += sum[i][i] * (m/i) + sum[i][m%i]; 32 } 33 printf("%.7lf\n",4.0*(ans+1)/(1ll * (n*2+1) * (m*2+1) - 1)); 34 } 35 return 0; 36 }//by tkys_Austin;
X Highways (枚举本质不同的线)
题意:给出一个n*m的点阵(n,m<=300),问有多少条非水平和非竖直的直线至少穿过两个点;
题解:
将线看成三角形的斜边,不重地统计它们;
先枚举本质不同的三角形(x,y)且(gcd(x,y)==1),有对称的情况所以答案乘2;
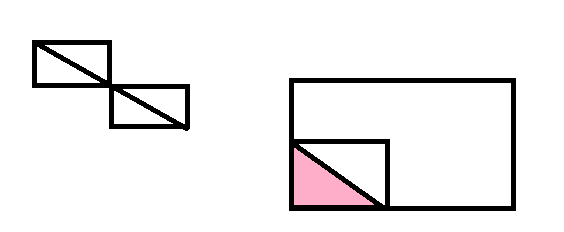
每个本来可以有(n-x)*(m-y)种放法,但是有可能出现图一的那种情况,然而有这样的情况两个矩形必不能重合(重合gcd(x,y)!=1),所以只要去掉(n-2*x)*(m-2*y)的区域就好了;


1 #include<cstdio> 2 #include<iostream> 3 #include<algorithm> 4 #include<cstring> 5 #include<queue> 6 #include<cmath> 7 #include<vector> 8 #include<stack> 9 #include<map> 10 #define Run(i,l,r) for(int i=l;i<=r;i++) 11 #define Don(i,l,r) for(int i=l;i>=r;i--) 12 #define ll long long 13 #define inf 0x3f3f3f3f 14 using namespace std; 15 const int N=310; 16 int n,m,vis[N][N]; 17 int gcd(int a,int b){return !b?a:gcd(b,a%b);} 18 void pre(){ 19 for(int i=1;i<=300;i++) 20 for(int j=1;j<=300;j++){ 21 if(gcd(i,j)==1)vis[i][j] = 1; else vis[i][j] = 0; 22 } 23 } 24 int main(){ 25 pre(); 26 while(~scanf("%d%d",&n,&m)){ 27 if(!n&&!m)break; 28 int sum = 0; 29 for(int i=1;i<n;i++) 30 for(int j=1;j<m;j++)if(vis[i][j]){ 31 sum += (n-i)*(m-j) - max(0,n-i*2)*max(0,m-j*2); 32 } 33 cout << sum*2 << endl; 34 } 35 return 0; 36 }//by tkys_Austin;
Y Magical GCD (gcd迭代的性质+链表)
题意:n个元素的序列a1,…an(ai<=1e12),求一个连续的子序列,使得它们的gcd*长度最大(n<=1e5);
题解:
gcd(x,y)|x , |y;
所以子序列的gcd 最多变化log2ai次;
枚举右端点,左端点用链表更新加查找;


1 #include<cstdio> 2 #include<iostream> 3 #include<algorithm> 4 #include<cstring> 5 #include<queue> 6 #include<cmath> 7 #include<vector> 8 #include<stack> 9 #include<map> 10 #define Run(i,l,r) for(int i=l;i<=r;i++) 11 #define Don(i,l,r) for(int i=l;i>=r;i--) 12 #define ll long long 13 #define inf 0x3f3f3f3f 14 using namespace std; 15 const int N=100010; 16 int n,pre[N],nxt[N]; 17 ll w[N],a[N]; 18 ll gcd(ll x,ll y){return !y?x:gcd(y,x%y);} 19 int main(){ 20 //freopen("Y.in","r",stdin); 21 //freopen("Y.out","w",stdout); 22 int T;scanf("%d",&T); 23 while(T--){ 24 scanf("%d",&n); 25 ll ans=0; 26 Run(i,1,n){ 27 scanf("%lld",&a[i]); 28 nxt[i] = i + 1; 29 pre[i] = i - 1; 30 w[i] = a[i]; 31 ans = max(ans,w[i]); 32 } 33 for(int i=1;i<=n;i++){ 34 for(int j=1;j!=i;j=nxt[j]){ 35 w[j] = gcd(w[j],a[i]); 36 ans = max(ans,w[j] * (i - j + 1)); 37 } 38 for(int j=i;j!=1;j=pre[j]){ 39 if(w[j]==w[pre[j]]){ 40 pre[nxt[j]]=pre[j]; 41 nxt[pre[j]]=nxt[j]; 42 } 43 } 44 } 45 printf("%lld\n",ans); 46 } 47 return 0; 48 }//by tkys_Austin;
Z Race (递推)
题意:可胜,可负,可平,问n个人赛马时的排名可能性;(n<=1e3)
题解:
设f(n)为n个人赛马的排名总数,枚举第一名;$$f(n) = \sum_{i=1}^{n}C_{n}^{i}f(n-i)$$


1 #include<cstdio> 2 #include<iostream> 3 #include<algorithm> 4 #include<cstring> 5 #include<queue> 6 #include<cmath> 7 #include<vector> 8 #include<stack> 9 #include<map> 10 #define Run(i,l,r) for(int i=l;i<=r;i++) 11 #define Don(i,l,r) for(int i=l;i>=r;i--) 12 #define ll long long 13 #define inf 0x3f3f3f3f 14 using namespace std; 15 const int N=1010,mod=10056; 16 int n,f[N],C[N][N]; 17 void pre(){ 18 for(int i=0;i<=1e3;i++)C[i][0]=1; 19 for(int i=1;i<=1e3;i++) 20 for(int j=1;j<=1e3;j++){ 21 C[i][j] = (C[i-1][j] + C[i-1][j-1]) %mod; 22 } 23 f[0]=1; 24 for(int i=1;i<=1e3;i++){ 25 f[i] = 0; 26 for(int j=1;j<=i;j++){ 27 f[i] = (f[i] + 1ll * C[i][j] * f[i-j] %mod) %mod; 28 } 29 } 30 } 31 int main(){ 32 pre(); 33 int T,Case=0;scanf("%d",&T); 34 while(T--){ 35 cin >> n; 36 cout << "Case " << ++Case << ": " << f[n] << endl; 37 } 38 return 0; 39 }//by tkys_Austin;







 本文精选了一系列算法竞赛题目,涵盖Fibonacci数列、组合数、欧拉函数、概率论等多个核心数学概念与算法,提供了详细的题解思路,旨在帮助读者深入理解算法背后的数学原理。
本文精选了一系列算法竞赛题目,涵盖Fibonacci数列、组合数、欧拉函数、概率论等多个核心数学概念与算法,提供了详细的题解思路,旨在帮助读者深入理解算法背后的数学原理。
















 906
906

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








