9.迷宫问题[第一版:递归]

最新推荐文章于 2020-08-04 09:53:31 发布

weixin_34107739

最新推荐文章于 2020-08-04 09:53:31 发布

阅读量107

点赞数

CC 4.0 BY-SA版权

文章标签：数据结构与算法

原文链接：http://www.cnblogs.com/tinaluo/p/5290216.html

本文介绍了一种简化迷宫求解问题的方法，通过使用3*3的二维数组来模拟迷宫，并采用递归算法进行路径搜索。详细解释了如何仅考虑下移和右移两种移动方向，最终到达出口作为可行路径。

先把问题做最大程度的简化，不用框一个50*50的大迷宫，只需要压缩在3*3的二维数组中模拟，这个弄清楚了，再大的也是一样。移动方向只包括下移和右移两种方式。先下移，再右移。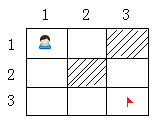
在这个二维数组中，约定规则：0表示通路，-1表示路径（可通过），1表示障碍物。于是得到一个二维数组的形式如下：（由于四周需要障碍物围墙，所以外围加了一层，即总共为：5*5的二维数组）

{
    {1,1,1,1,1},
    {1,0,0,1,1},
    {1,0,1,0,1},
    {1,0,0,0,1},
    {1,1,1,1,1}
}

由于只能下移和右移，这就很类似于二叉树的先序遍历，所以用递归形式：

   if (maze[x + 1][y] == 0) //下移
      pass(x + 1, y); 
   if (maze[x][y + 1] == 0) //右移
      pass(x, y + 1);

直接看图表示清晰：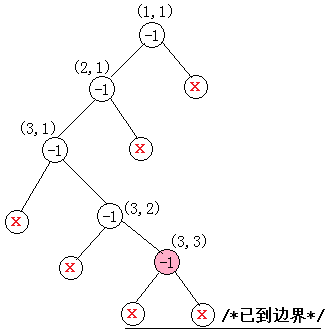

递归最后的约束条件为最后移动到的坐标=目标坐标，即是一种可行的方式。代码如下：

/*-----完整代码@映雪-------*/

#include <iostream>
using namespace std;
#define MAXROW 5
int maze[MAXROW][MAXROW] = {
    {1,1,1,1,1},
    {1,0,0,1,1},
    {1,0,1,0,1},
    {1,0,0,0,1},
    {1,1,1,1,1}
}; //迷宫数组 
int InX = 1, InY = 1;        // 入口
int OutX = MAXROW-2,OutY = MAXROW-2    ;    // 出口
void print()
{
   for (int i = 0; i < MAXROW; i++)
   {
      for (int j = 0; j < MAXROW; j++)
      {
         if (maze[i][j] == 1)
           cout<<"█";
         else if (maze[i][j] == -1)
            cout<<"◇";
         else
            cout<<"  ";
       }
      cout<<endl; /*换行*/
  } 
}
void pass(int x, int y)
{
   maze[x][y] = -1; //初始设该位置可通过 
   if (x == OutX && y == OutY) //若已到终点 
   {
      print();
   }
    if (maze[x + 1][y] == 0)/*下移*/
      pass(x + 1, y); 
    if (maze[x][y + 1] == 0)/*右移*/
      pass(x, y + 1); 
   maze[x][y] = 0;
}
int main(void)
{
   print();
   pass(InX, InY);
   return 0;
}

转载于:https://www.cnblogs.com/tinaluo/p/5290216.html