x为正变数，求y=x^3/(x^4+4)的最大值

最新推荐文章于 2025-08-13 21:05:35 发布

weixin_34080903

最新推荐文章于 2025-08-13 21:05:35 发布

阅读量478

点赞数

文章标签： javascript ViewUI

本文通过数学分析找到给定函数的极值，并利用HTML5 Canvas绘制该函数的图像，展示了函数图像的绘制过程及如何使用JavaScript进行数学运算。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

设z=1/y=x⁴+4/x³

显然，当z有最小值时，y有最大值，求得z_min，就得到了y_max

而z=x+4/x³=x/3+x/3+x/3+4/x³

根据正实数算术平均数大于等于它们的几何平均数的定理

当x/3=4/x³时，有z_min，此时x=12^1/4

因此，y_max=12^1/4/16≈0.40296

图线如下：

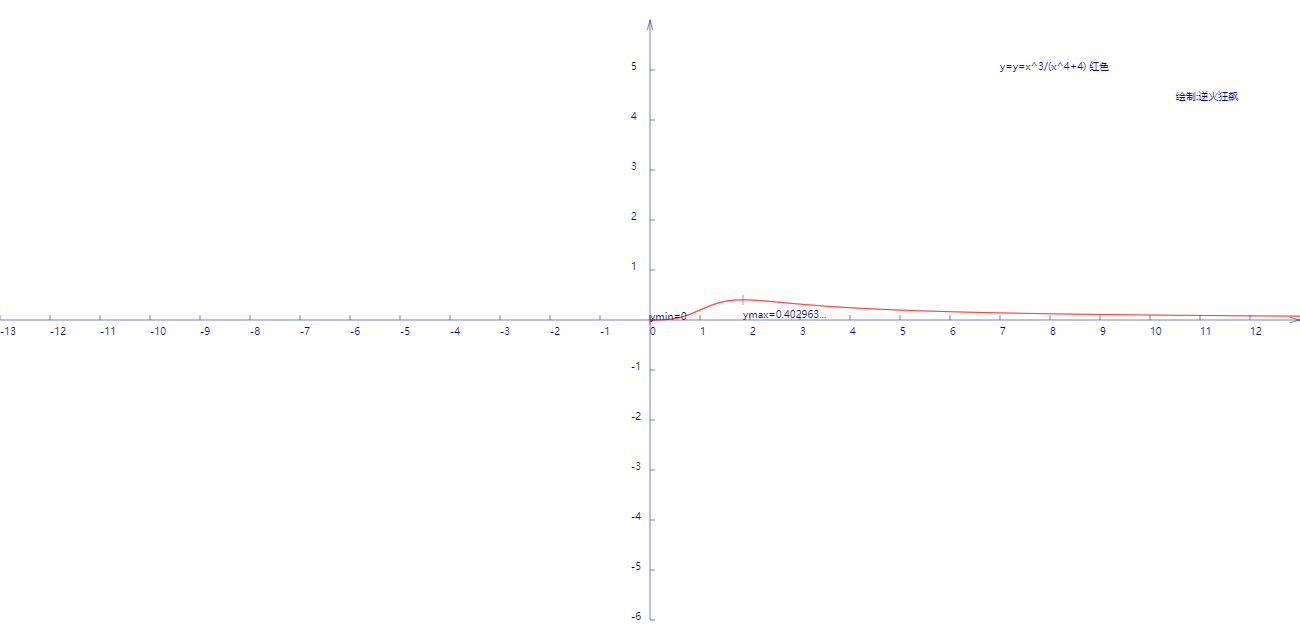
代码如下：

<!DOCTYPE html>
<html lang="utf-8">
<meta http-equiv="Content-Type" content="text/html; charset=utf-8"/>
<head>
     <title>绘制y=x^3/(x^4+4)曲线</title>
    </head>

     <body onload="draw()">
        <canvas id="myCanvus" width="1300px" height="640px" style="border:1px dashed black;">
            出现文字表示你的浏览器不支持HTML5
        </canvas>
     </body>
</html>
<script type="text/javascript">
<!--
    function draw(){
        var canvas=document.getElementById("myCanvus");
        var canvasWidth=1300;
        var canvasHeight=640;

        var context=canvas.getContext("2d");
        
        context.fillStyle = "white";
        context.fillRect(0, 0, canvasWidth, canvasHeight);

        context.strokeStyle = "black";
        context.fillStyle = "black";

        
        // 进行坐标变换：把原点放在左下角，东方为X轴正向，北方为Y轴正向
        var offsetY=320;// Y向偏移值，正值向上偏，用来画坐标轴
        var offsetX=650;// X向偏移值，正值向右偏，用来画坐标轴

        context.save();
        context.translate(0+offsetX,canvasHeight-offsetY);

        drawAxisXText(context);// 文字和线分开画比较好处理
        drawAxisYText(context);
        drawTitleText(context);

        context.rotate(getRad(180));
        context.scale(-1,1);        

        drawAxisX(context);        
        drawAxisY(context);       
        drawCurve(context);       

        context.restore();        
    }

    function drawTitleText(ctx){        
        ctx.lineWidth=0.5;
        ctx.strokeStyle='navy';
        ctx.fillStyle='navy';

        var x=350;
        var y=-250;

        // 写文字
        ctx.fillText("y=y=x^3/(x^4+4) 红色",x,y);    
        //ctx.fillText("y=(x-3)^3 绿色",x,y+20);    
        //ctx.fillText("y=(x-5)^4 黄色",x,y+40);    
        //ctx.fillText("y=(x-7)^5 青柠色",x,y+60);    
        //ctx.fillText("y=(x+3)^0.5 紫色",x,y+80);
        //ctx.fillText("y=(x+5)^0.33 栗色",x,y+100);

        ctx.fillText("  绘制:逆火狂飙",x+170,y+30);
    }

    function drawCurve(ctx){
        var cds=[{}];
        var cds1=[{}];
        var cds2=[{}];
        var cds3=[{}];
        var cds4=[{}];
        var cds5=[{}];
        var cds6=[{}];

        var x,y,arr;
        for(x=0;x<=13;x+=0.01){    
            y=Math.pow(x,3)/(Math.pow(x,4)+4);//
            arr={"x":x,"y":y};
            cds.push(arr);
        }

        paintCurve(ctx,"red",cds);
        //paintCurve(ctx,"green",cds1);
        //paintCurve(ctx,"yellow",cds2);
        //paintCurve(ctx,"lime",cds3);
        //paintCurve(ctx,"purple",cds4);
        //paintCurve(ctx,"maroon",cds5);
        //paintCurve(ctx,"maroon",cds6);*/

        var ymax=-1000,ymin=1000,xmax,xmin;
        for(var i=0; i<cds.length; i++){  
            // 求y最大值
            if(cds[i].x>0 && cds[i].y>ymax){
                ymax=cds[i].y;
                xmax=cds[i].x;
            }

            // 求y最小值
            if(cds[i].x>=0 && cds[i].y<ymin){
                ymin=cds[i].y;
                xmin=cds[i].x;
            }
        } 

        console.log("ymin="+ymin+" xmin="+xmin+" ymax="+ymax+" ymin="+ymin+" xmax="+xmax);
        var SU=50;// Scale Unit
        // 极大值
        ctx.beginPath();
        ctx.moveTo(xmax*SU,ymax*SU-5);
        ctx.lineTo(xmax*SU,ymax*SU+5);

        ctx.save();
        ctx.scale(1,-1);
        ctx.fillText("ymax="+cutShort(ymax.toString(),8),xmax*SU,-ymax*5);
        ctx.restore();

        ctx.stroke();
        ctx.closePath();

        // 极小值
        ctx.beginPath();
        ctx.moveTo(xmin*SU,ymin*SU-5);
        ctx.lineTo(xmin*SU,ymin*SU+5);

        ctx.save();
        ctx.scale(1,-1);
        ctx.fillText("ymin="+ymin,xmin*SU,-ymin*5);
        ctx.restore();

        ctx.stroke();
        ctx.closePath();

        
    }

    function paintCurve(ctx,color,cds){
        var SU=50;// Scale Unit

        ctx.strokeStyle = color;
        ctx.beginPath();        
        for(var i=0; i<cds.length; i++){  
            ctx.lineTo(cds[i].x*SU,cds[i].y*SU);// 注意y轴比例
        }         
        ctx.stroke();
        ctx.closePath();
    }

    function drawAxisX(ctx){
        ctx.save();
        
        ctx.lineWidth=0.5;
        ctx.strokeStyle='navy';
        ctx.fillStyle='navy';

        var start=-650;
        var end=650;

        // 画轴
        ctx.beginPath();
        ctx.moveTo(start, 0);
        ctx.lineTo(end, 0);
        ctx.stroke();
        ctx.closePath();

        // 画箭头
        ctx.beginPath();
        ctx.moveTo(end-Math.cos(getRad(15))*10, Math.sin(getRad(15))*10);
        ctx.lineTo(end, 0);
        ctx.lineTo(end-Math.cos(getRad(15))*10, -Math.sin(getRad(15))*10);
        ctx.stroke();
        ctx.closePath();
        
        // 画刻度
        var x,y;
        y=5;
        for(x=start;x<end;x+=50){
            ctx.beginPath();
            ctx.moveTo(x, 0);
            ctx.lineTo(x, y);
            
            ctx.stroke();
            ctx.closePath();
        }

        ctx.restore();
    }

    function drawAxisXText(ctx){        
        ctx.lineWidth=0.5;
        ctx.strokeStyle='navy';
        ctx.fillStyle='navy';

        var start=-650;
        var end=650;

        // 写文字
        var x,y=5;
        for(x=start;x<end;x+=50){
            ctx.fillText(x/50,x,y+10);
        }
    }

    function drawAxisY(ctx){
        ctx.save();
        
        ctx.lineWidth=0.5;
        ctx.strokeStyle='navy';
        ctx.fillStyle='navy';

        var start=-300;
        var end=300;

        // 画轴
        ctx.beginPath();
        ctx.moveTo(0, start);
        ctx.lineTo(0, end);
        ctx.stroke();
        ctx.closePath();

        // 画箭头
        ctx.beginPath();
        ctx.moveTo(Math.sin(getRad(15))*10, end-Math.cos(getRad(15))*10);
        ctx.lineTo(0, end);
        ctx.lineTo(-Math.sin(getRad(15))*10, end-Math.cos(getRad(15))*10);
        ctx.stroke();
        ctx.closePath();
        
        // 画刻度
        var x,y;
        x=5;
        for(y=start;y<end;y+=50){// 注意y轴比例
            ctx.beginPath();
            ctx.moveTo(x, y);
            ctx.lineTo(0, y);
            
            ctx.stroke();
            ctx.closePath();
        }
    }

    function drawAxisYText(ctx){        
        ctx.lineWidth=0.5;
        ctx.strokeStyle='navy';
        ctx.fillStyle='navy';

        var start=-250;
        var end=350;

        // 写文字
        var x=-19,y=5;
        for(y=start;y<end;y+=50){

            if(y!=0){
                ctx.fillText(-y/50,x,y);// 注意y轴比例
            }
        }
    }

    function getRad(degree){
        return degree/180*Math.PI;
    }

    function cutShort(str,length){
        if(str.length>length){
            str=str.substr(0,length)+"...";
        }
        
        return str;
    }
//-->
</script>