算法题一道

前言：下面的截图来自一个朋友的面试题，对于第四题，本人虽然愚拙，但还是花了点时间，写出了算法实现，以及图片展示我的算法思路：

粗略的代码实现：

 1 #import <Foundation/Foundation.h>
 2 
 3 #define hhPrint(m,n) printf("(%d,%d)\t",m,n)
 4 #define hPrint(m,n,hy) printf("(%d,%d)%d\t",m,n,hy)
 5 #define table printf("\n");
 6 
 7 
 8 void printMatrix(int arrMax[3][4],int m,int n){
 9     
10     NSLog(@"然后对角打印");
11     // 要计算和获得行和列的最大值
12     int maxLength = m > n?m:n;
13     int temp = maxLength * 2 -1;
14     for (int i = 0; i < temp; i++) {
15         if (i < n) {
16             hPrint(0,i,arrMax[0][i]);
17         }
18         for (int j = 1; j< i+1; j++) {
19             int left = j;
20             int right = i-j;
21 
22             // 左下标小于行数，右下标小于列数
23             if (left < m && right < n) {
24                 hPrint(j,i-j,arrMax[j][i-j]);
25             }
26         }
27         table
28     }
29 }
30 
31 int main(int argc, const char * argv[]) {
32     @autoreleasepool {
33         int arr[3][4] =
34         {
35             {
36                 1,2,3,4
37             },
38             {
39                 5,6,7,8
40             },
41             {
42                 9,10,11,12
43             }
44         };
45         
46         printMatrix(arr,3,4);
47     }
48     return 0;
49 }

算法思路截图：

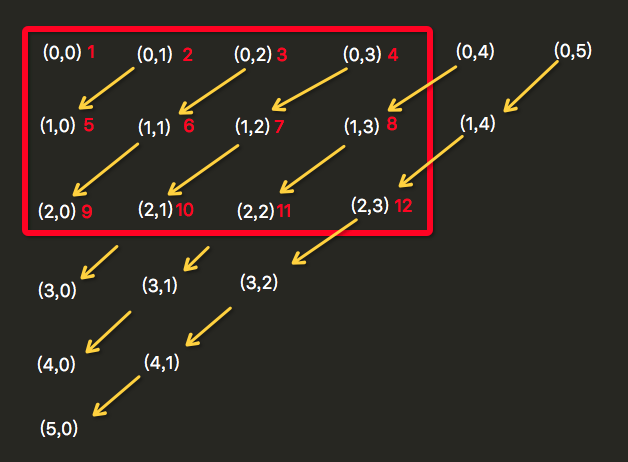
算法思路讲解：

　①、根据二维数组，我们在图中可以全部列出来就是一个矩阵（比如上图三行四列的二维数组，我用红色框框起来的部分），然后我们可以通过"行数+列数-1"得到图上大三角形的第一行的个数，假设为n。按照上面图的意思，n = 6。

　②、根据n，我们当然可以直接打印这第一行的所有坐标，毕竟他们的横坐标都是0。

　③、根据第一行的每一个坐标，我们都可以再添加一个for循环遍历得到他们左下角的数字。上面用黄色箭头示意，比如(0,2)可以得到(1,1)，然后还可以得到(2,0)。

　④、之所以需要第①步中"行数+列数-1"，是因为如果只用"行数"的话，比如上图的(1,3),(2,2),(3,1)就不好得到了，虽然一定有方法可以得到，不过我想不出更简便的方法了。

　⑤、接着，通过第一行的行数"行数+列数-1"，我可以得到上面图中大三角形所有的坐标，并且可以按照上面黄色箭头的顺序全部打印输出。

　⑥、然后，需要排除掉不需要的部分，所以在代码中，我用了if语句排除，横坐标不要超过行数，纵坐标不要超过列数。

　⑦、最后，根据坐标打印数组中对应的数即可。