奇异值分解SVD

2019独角兽企业重金招聘Python工程师标准>>>

        要理解奇异值分解SVD(Singular Value Decomposition)，首先理解特征值分解。

特征值分解：

        矩阵的特征公式如下：，几何上的解释是，原始空间的向量x经过矩阵M变换后，只有长度上的变换，没有方向上的变化，伸缩的比例为λ。

        数学上，M是一个nxn的实对称矩阵，x是一个n维向量，那么x就是M的一个特征向量，λ称为特征向量x对应的一个特征值。如果M对应的n个特征值λ1，λ2… λn对应的n个特征向量为{w1, w2 … wn}，则M矩阵可以进行特征分解：

        M = W

其中，W是n个特征向量组成的特征矩阵， 是由特征值组成的对角矩阵。如果W被标准化，即W的每个特征向量的L2范数等于1，即=1，此时，W的各个向量组成一组标准正交基。这样M特征分解也可以写成：

        M = W

以上特征值分解的矩阵M是n行n列的方阵。如果M不是n阶方阵，而是mxn的矩阵，是否也可以进行分解？答案是可以，并且这个分解就叫做奇异值分解。

奇异值分解：

        M = U

        其中M是mxn矩阵，U是mxm方阵，V是nxn方阵， 是mxn对角阵。可以证明：

1. V是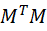方阵的nxn特征矩阵（列向量是特征向量）
2. U是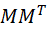方阵的mxm特征矩阵（列向量是特征向量）
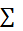3. 是每个每个奇异值的对角阵，其中每个奇异值是相应特征值的平方根，即δi = λi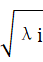

证明如下：

       

                  = V，其中 ==I

        由此，可以看出V是的特征矩阵，奇异值是特征值的平方根。同理，U是的特征矩阵。

综上，mxn矩阵的奇异值分解步骤如下：

1. 求出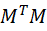的特征值和特征向量V
2. 求出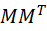的特征值和特征向量U
3. 求出个非零特征值的平方根作为相应的奇异值，组合成

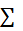
最后M = U。

转载于:https://my.oschina.net/yepanl/blog/3045120