Proximal Algorithms 4 Algorithms

Proximal Algorithms

这一节介绍了一些利用proximal的算法.

Proximal minimization

这个相当的简单, 之前也提过，就是一个依赖不动点的迭代方法: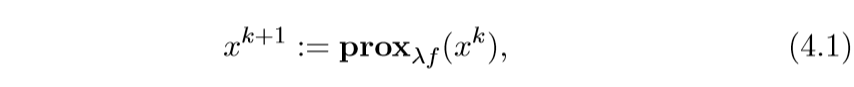

有些时候\(\lambda\)不是固定的:
\[ x^{k+1} := \mathbf{prox}_{\lambda^k f}(x^k), \sum_{k=1}^{\infty}\lambda^k = \infty \]

import numpy as np
import matplotlib.pyplot as plt 

以\(f(x,y) = x^2 + 50y\)为例

f = lambda x: x[0] ** 2 + 50 * x[1] ** 2
x = np.linspace(-40, 40, 1000)
y = np.linspace(-20, 20, 500)
X, Y = np.meshgrid(x, y) #获取坐标
fig, ax = plt.subplots()
ax.contour(X, Y, f([X, Y]), colors="black")
plt.show()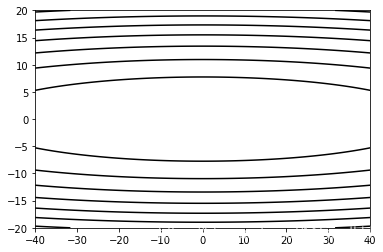

求解proximal可得:
\[ x = \frac{v_1}{2\lambda + 1} \\ y = \frac{v_2}{100\lambda + 1} \]

def prox(v1, v2, lam):
    x = v1 / (2 * lam + 1)
    y = v2 / (100 * lam + 1)
    return x, y

times = 50
x = 30
y = 15
lam = 0.1
process = [(x, y)]
for i in range(times):
    x, y = prox(x, y, 0.1)
    process.append((x, y))

process = np.array(process)
x = np.linspace(-40, 40, 1000)
y = np.linspace(-20, 20, 500)
X, Y = np.meshgrid(x, y) #获取坐标
fig, ax = plt.subplots()
ax.contour(X, Y, f([X, Y]), colors="black")
ax.scatter(process[:, 0], process[:, 1])
ax.plot(process[:, 0], process[:, 1])
plt.show()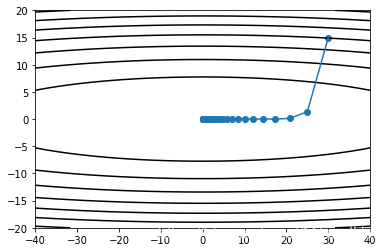

解释

除了之前已经提到过的一些解释：

Gradient flow

考虑下面的微分方程: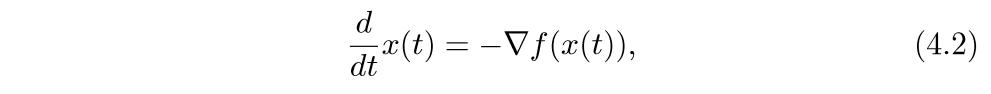

\(t \rightarrow \infty\)时\(f(x(t))\rightarrow p^*\)，其中\(p^*\)是最小值.
我们来看其离散的情形: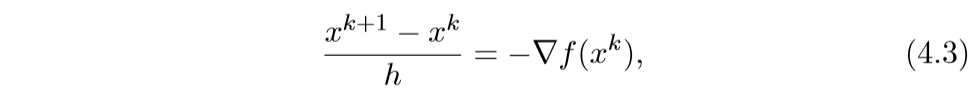

于是就有：
\[ x^{k+1} := x^k - h \nabla f(x^k) \]

还有一种后退的形式:
\[ \frac{x^{k+1}-x^k}{h}=-\nabla f(x^{k+1}) \]
此时，为了找到\(x^{k+1}\), 我们需要求解一个方程:
\[ x^{k+1} + h \nabla f(x^{k+1}) = x^k \\ \Rightarrow x^{k+1} = (I+ h \nabla f)^{-1}x^k = \mathbf{prox}_{hf}(x^k) \]

还有一种特殊的解释，这里不提了.

\(f(x) + g(x)\)

考虑下面的问题:
\[ \mathrm{minimize} \quad f(x) + g(x) \]
其中\(f\)是可微的.
我们可以通过下列proximal gradient method来求解:
\[ x^{k+1} := \mathbf{prox}_{\lambda^k g}(x^k - \lambda^k \nabla f(x^k)) \]
可以证明(虽然我不会)，当\(\nabla f\) Lipschitz连续，常数为\(L\)，那么，如果\(\lambda^k = \lambda \in (0, 1/L]\)，这个方法会以\(O(1/k)\)的速度收敛.

还有一些直线搜素算法:

一般取\(\beta=1/2\)，\(\widehat{f}_{\lambda}\)是\(f\)的一个上界，在后面的解释中在具体探讨.

解释1 最大最小算法

最大最小算法， 最小化函数\(\varphi: \mathbb{R}^n \rightarrow \mathbb{R}\):
\[ x^{k+1} := \mathrm{argmin}_x \widehat{\varphi}(x, x^k) \]
其中\(\widehat{\varphi}(\cdot, x^k)\)是\(\varphi\)的凸上界:\(\widehat{\varphi}(x, x^k) \ge \varphi(x)\), \(\widehat{\varphi}(x, x)=\varphi(x)\).
我们可以这么构造一个上界: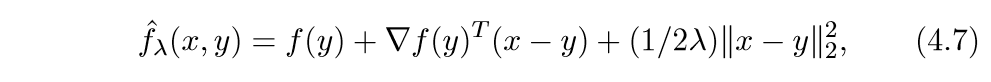

上面的式子很像泰勒二阶展开，首先这个函数符合第二个条件，下面我们证明，当\(\lambda \in (0, 1/L]\)，那么它也符合第一个条件.
\[ \widehat{f}_{\lambda}(x) - f(x) = f(y) - f(x) +\nabla f(y)^T(x-y)+...=(\nabla f(y)-\nabla f(z))(x-y)+... \]
其中\(z = x + \theta (y-x), \theta \in [0, 1]\), 又Lipschitz连续，所以:
\[ \|\nabla f(y)-\nabla f(z)\| \le L\|y-z\|\le L\|y-x\| \]
考虑\(f(x+t\Delta x)\)关于\(t\)的二阶泰勒展式:
\[ f(x+t\Delta x) = f(x)+\nabla f(x)^T\Delta x t + \frac{1}{2}\Delta x^T \nabla^2f(x) \Delta x t^2 + o(t^2) \]
令\(t=1\):
\[ f(x+\Delta x) = f(x)+\nabla f(x)^T\Delta x + \frac{1}{2}\Delta x^T \nabla^2f(x) \Delta x + ... \]
\[ \frac{\|\nabla f(x)-\nabla f(x+t\Delta x)\|}{t}\le L\|\Delta x\| \]
由当\(t \rightarrow 0\)时，左边为\(\|\nabla^2 f(x) \Delta x\|\), 所以\(\nabla^2 f(x)\)的最大特征值必小于\(L\), 所以:
\[ f(x+\Delta x) \le f(x)+\nabla f(x)^T\Delta x + \frac{L}{2}\|\Delta x\|_2^2 + ... \]
完蛋，好像只能证明在局部成立，能证明在全局成立吗？

\[ x^{k+1} := \mathrm{argmin}_x \widehat{f}_{\lambda}(x, x^k) \]
再令：
\[ q_{\lambda}(x, y)=\widehat{f}_{\lambda}(x,y) + g(x) \]
那么:
\[ x^{k+1} := \mathrm{argmin}_x q_{\lambda}(x, x^k)=\mathbf{prox}_{\lambda g}(x^k-\lambda \nabla f(x^k)) \]
上面的等式，可以利用第二节中的性质推出.

不动点解释

最小化\(f(x)+g(x)\)的点\(x^*\)应当满足:
\[ 0 \in \nabla f(x^*)+\partial g(x^*) \]
更一般地: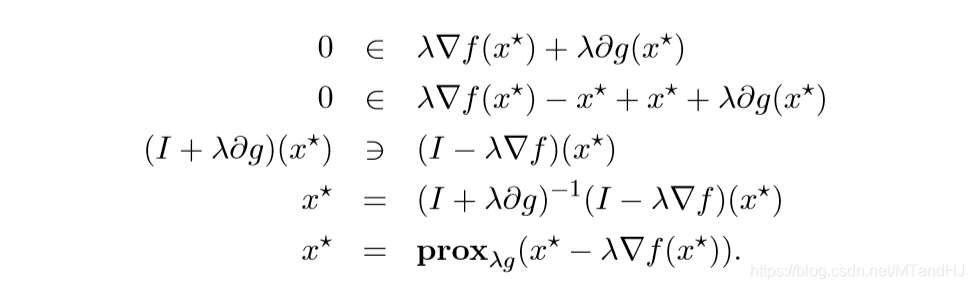

这便说明了一种迭代方式.

Forward-backward 迭代解释

考虑下列微分方程系统: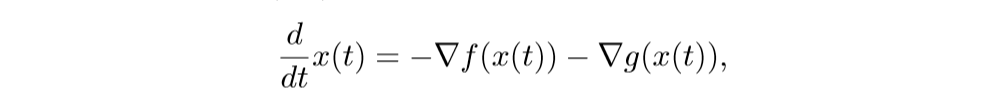

离散化后得: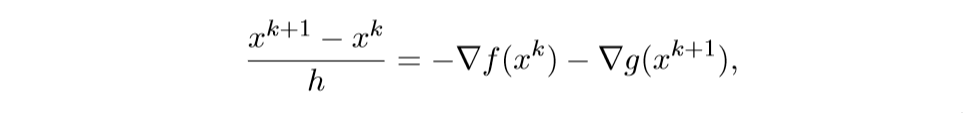

注意，等式右边\(x^k\)和\(x^{k+1}\)，这正是巧妙之处.
解此方程可得: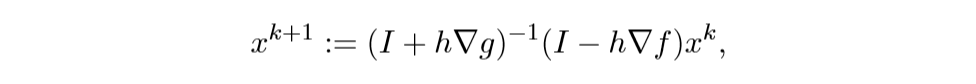

这就是之前的那个迭代方法.

加速 proximal gradient method

其迭代方式为:
\[ y^{k+1} := x^k + w^k(x^k-x^{k-1}) \\ x^{k+1} := \mathbf{prox}_{\lambda^k g}(y^{k+1}-\lambda^k \nabla f(y^{k+1})) \]
\(w^k \in [0,1)\)
这个方法有点类似Momentum的感觉.
一个选择是:
\[ w^k = \frac{k}{k+3} \]
也有类似的直线搜索算法:

交替方向方法 ADMM

alternating direction method of multipliers (ADMM), 怎么说呢，久闻大名，不过还没看过类似的文章.
同样是考虑这个问题:
\[ \mathrm{minimize} \quad f(x) + g(x) \]
但是呢，这时\(f,g\)都不一定是可微的, ADMM采取的策略是:
\[ x^{k+1} := \mathbf{prox}_{\lambda f} (z^k - u^k) \\ z^{k+1} := \mathbf{prox}_{\lambda g} (x^{k+1} + u^k)\\ u^{k+1} := u^k + x^{k+1} -z^{k+1} \]

特殊的情况是, \(f\)或\(g\)是指示函数，不妨设\(f\)是闭凸集\(\mathcal{C}\)的指示函数，而\(g\)是闭凸集\(\mathcal{D}\)的指示函数, 即:
\[ I_{\mathcal{C}}(x)=0, if \: x\in \mathcal{C}, else \: + \infty \]
这个时候，更新公式变为:
\[ x^{k+1} := \Pi_{\mathcal{C}} (z^k - u^k)\\ z^{k+1} := \Pi_{\mathcal{C}} (x^{k+1} + u^k) \\ u^{k+1} := u^k + x^{k+1} -z^{k+1} \]

解释1 自动控制

可以这么理解，\(z\)为状态，而\(u\)为控制，前俩步时离散时间动态系统(不懂啊...)， 第三步的目标是选择\(u\)使得\(x=z\)，所以\(x^{k+1}-z^{k+1}\)可以认为是一个信号误差，所以第三步就会把这些误差累计起来.

解释2 Augmented Largranians

我们可以将问题转化为: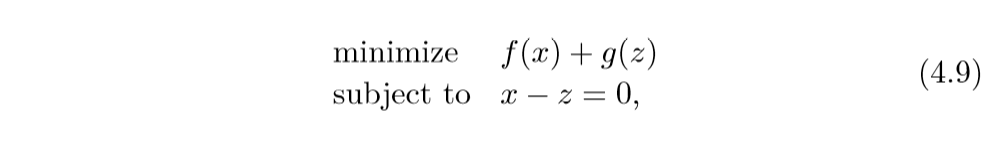

augmented Largranian: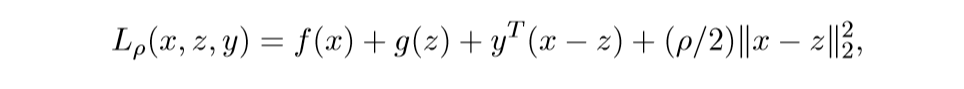

其中\(y\)为对偶变量.
在\(z, y\)已知的条件下，最小化\(L\), 即:
\[ x^{k+1} := \mathrm{argmin}_x L_{\rho}(x, z^k, y^k) \]
在\(x, y\)已知的条件下，最小化\(L\), 即:
\[ z^{k+1} := \mathrm{argmin}_z L_{\rho}(x^{k+1}, z, y^k) \]
最后一步:
\[ y^{k+1} := y^k + \rho (x^{k+1} - z^{k+1}） \]
如果依照对偶问题的知识，关于\(y\)应该是取最大，但是呢，关于\(y\)是一个仿射函数，所以没有最值，所以就简单地取那个？
注意到：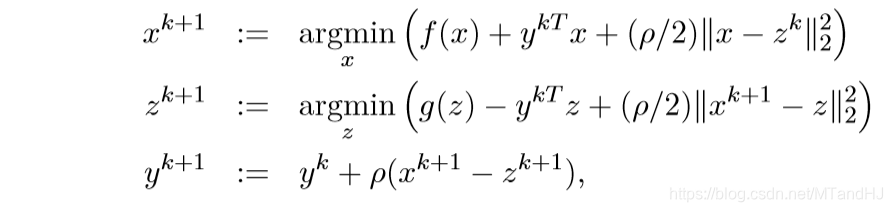


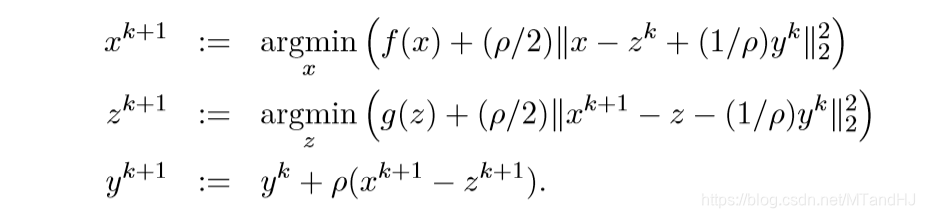
让\(u^k = (1/\rho)y^k\), \(\lambda = 1/\rho\)就是最开始的结果.

解释3 Flow interpretation

问题(4.9)的最优条件(KKT条件):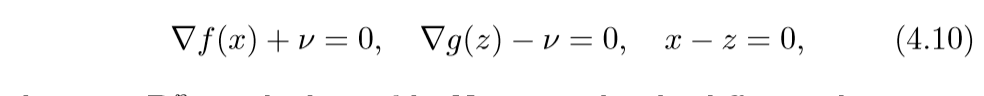

其中\(v\)是对偶变量.考虑微分方程：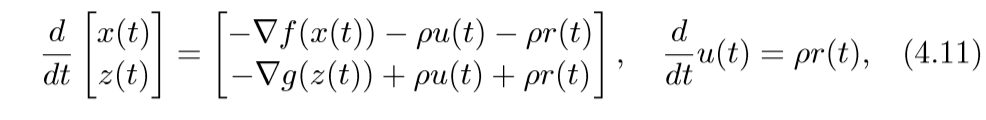

(4.11)取得稳定点的条件即为(4.10)(\(v=\rho)\)(这部分没怎么弄明白).
离散化情形为: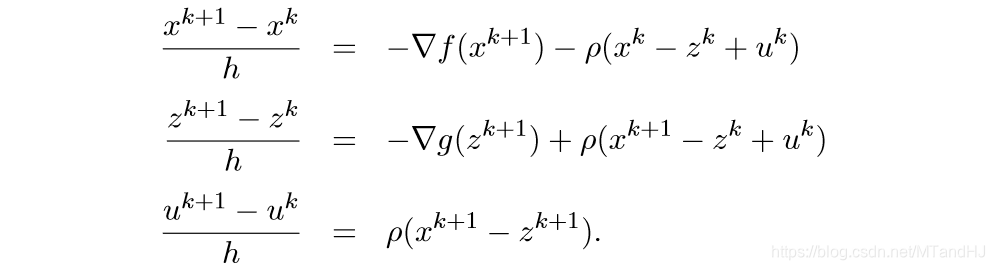

取\(h = \lambda, \rho = 1/\lambda\)即可得ADMM.

解释4 不动点

原问题的最优条件为:
\[ 0 \in \partial f(x^*) + \partial g(x^*) \]

ADMM的不动点满足：
\[ x = \mathbf{prox}_{\lambda f} (x-u), \quad z = \mathbf{prox}_{\lambda g}(x+u), \quad u = u + x - z \]
从最后一个等式，我们可以知道:
\[ x = z \], 于是
\[ x = \mathbf{prox}_{\lambda f}(x - u), \quad x = \mathbf{prox}_{\lambda g}(x + u) \]
等价于:
\[ x = (I + \partial f)^{-1}(x - u), x = (I + \lambda \partial g)^{-1}(x + u) \]
等价于:
\[ x - u \in x + \lambda \partial f(x), \quad x + u \in x + \lambda \partial g(x) \]
俩个式子相加，说明\(x\)即为最优解.
再来说明一下，为什么可以相加，根据次梯度的定义:
\[ \lambda f(z) \ge \lambda f(x) + (-u)^T(z-x), \quad \forall z\in \mathbf{dom}f \\ \lambda g(z) \ge \lambda g(x) + (+u)^T(z-x), \quad \forall z\in \mathbf{dom}g \\ \]
相加可得:
\[ \lambda f(z) + \lambda g(z) \ge 2x + \lambda f(x) +\lambda g(x) + 0 \]
需要注意的是，我证明的时候也困扰了，
\[ x - u \in x + \lambda \partial f(x) \]
并不是指(x-u)是函数\(x^2/2 + \lambda f(x)\)的次梯度, 而是\(x-u\)在\(\lambda f(x)\)的次梯度集合加上\(x\)的集合内，也就是\(-u\)是其次梯度.

对不起！又想当然了，其实没问题, 如果
\[ g \in \partial f_1(x) + h(x) \]
而\(\partial f_2(x)=h(x)\)则:
\[ g \in \partial (f_1+f_2)(x) \]
证:
已知:
\[ f_1(z) \ge f_1(x)+\partial f_1(x)^T(z-x) \\ f_2(z) \ge f_2(x)+h(x)^T(z-x) \\ \]
俩式相加可得:
\[ (f_1+f_2)(z)\ge (f_1+f_2)(x) +(\partial f_1(x) + h(x))^T(z-x)=(f_1+f_2)(x) +g^T(z-x) \]
所以\(g \in \partial (f_1+f_2)(x)\), 注意\(g=g(x)\)也是无妨的.

特别的情况 \(f(x) + g(Ax)\)

考虑下面的问题：
\[ \mathrm{minimize} \quad f(x) + g(Ax) \]
上面的求解，也可以让\(\widetilde{g}(x) = g(Ax)\)，这样子就可以用普通的ADMM来求解了, 但是有更加简便的方法.

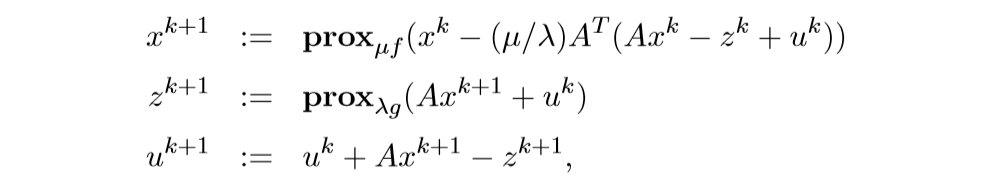
这个的来源为：

再利用和之前一样的推导，不过，我要存疑的一点是最后的替代，我觉得应该是:
\[ \rho (A^TAx^k - A^T z^k)^T x + (1 / 2\mu) \|x-x^k\|_2^2 \]
否则推不出来啊.

转载于:https://www.cnblogs.com/MTandHJ/p/10994811.html