一天一练之算法——约瑟夫问题

为什么80%的码农都做不了架构师？>>>   

猴子选王

一堆猴子都有编号，编号是1，2，3 ...m，这群猴子（m个）按照1-m的顺序围坐一圈，从第1开始数，每数到第N个，该猴子就要离开此圈，这样依次下来，直到圈中只剩下最后一只猴子，则该猴子为大王。

#include <stdio.h>
#include <stdlib.h>

int JosephusFun(int nAllCount,int nStep)
{
	int *npIndex=NULL , i=0 ,nCount=0;

	npIndex=(int *)malloc(sizeof(int)*nAllCount);

	for (i=0;i<nAllCount;i++)
	{
		npIndex[i]=i+1;
	}
	//打印报数前的顺序
	printf("报数前序号为：");
	for (i=0;i<nAllCount;i++)
	{
		printf("%d",npIndex[i]);
		printf("  ");
	}
	printf("\n");

	printf("=======================================\n");
	printf("报数出列顺序为：\n");
	i=-1;
	while(nCount<nAllCount)        //全部出列后循环结束
	{
		int nIndex=0 ;

		while(nIndex<nStep)        //报数等于步距时出列
		{
			i=(i+1)%nAllCount;      //循环报数

			if (npIndex[i]==0)      //如果当前序号已出列，则下一位报数
			{
				continue;
			}
			nIndex++;              //报数一次
		}

		//打印当前出列的编号
		printf("第%d个出列的为:%d\n",nCount+1,npIndex[i]);
		npIndex[i]=0;
		nCount++;
	}
	printf("=======================================\n");

	return 0;
}

int main()
{
	int nAllCount=0,nStep=0;

	printf("请输入总个数：");
	scanf("%d",&nAllCount);
	
	printf("请输入出列步长：");
	scanf("%d",&nStep);
	printf("\n");

	JosephusFun(nAllCount,nStep);

	return 0;
}

 测试如下：

 

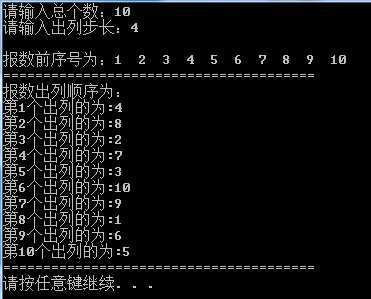
约瑟夫问题演变：

约瑟夫环 问题描述：约瑟夫问题的一种描述是：编号为1，2，…，n的n个人按顺时针方向围坐一圈，每人持一个密码（正整数）。一开始任选一个正整数作为报数上限值m，从第一个人开始按顺时针方向自1开始顺序报数，报到m时停止报数。报m的人出列，将他的密码作为新的m值，从他在顺时针方向上的下一个人开始重新从1报数，如此下去，直至所有人全部出列为止。试设计一个程序求出出列顺序。 基本要求 利用单向循环链表存储结构模拟此过程，按照出列的顺序印出各人的编号。 测试数据 M的初值为20；n=7，7各人的密码依次为3，1，7，2，4，8，4，首先m值为6（正确出栈顺序为6，1，4，7，2，3，5） 

转载于:https://my.oschina.net/871120/blog/309595