布点算法的作用是将已知的图结构以较美观的形式展示出来,需要尽量遵循的原则有五个:
- 对称性:绘制网络对应将具有相同结构的子图围绕绘图中心平衡布局
- 正交性:绘制网格对应的以网格为背景,并尽量将节点布局在网格交叉处,使边可以沿着网格线绘制。
- 连接角最大化原则,使同一节点任意两条边形成的角度尽量大
- 边交叉数量最小原则(最重要):绘图时应尽量减少相互交叉边的数量。
- 直线边原则:边尽量直线,避免曲线
布点算法之力导引布局
力导引布局的方法可以产生相当优美的网络布局,并充分展现网络的整体结构及其自同构特征。该方法最早由Eades在1984年提出。其基本思想是将网络看成一个顶点为钢环,边为弹簧的物理系统,系统被赋予某个初始状态以后,弹簧弹力(引力和斥力)的作用会导致钢环移动,这种运动直到系统总能量减少到最小值停止。每次循环都要计算任意一对点的斥力和相邻两个点的引力,计算复杂度为O(N2)
Kamada和Kawai改进了Eades的弹簧模型,提出KK算法。KK算法主要通过求系统的总能量: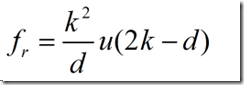 的最小值来确定节点的位置。其中Pi和pj 表示节点vi和vj的位置,lij表示vi和vj之间的弹簧的初始长度,kij表示弹性系数。在此模型中遵循了胡克定律。KK算法中加入了非相邻节点间理想距离的概念,两个节点的理想距离和它们之间的最短路径的长度成正比。当系统处于稳定状态时,弹簧的距离接近与他们的理想距离。KK算法的复杂度依然是N2,但是在收敛性方面得到了很大的提高。
的最小值来确定节点的位置。其中Pi和pj 表示节点vi和vj的位置,lij表示vi和vj之间的弹簧的初始长度,kij表示弹性系数。在此模型中遵循了胡克定律。KK算法中加入了非相邻节点间理想距离的概念,两个节点的理想距离和它们之间的最短路径的长度成正比。当系统处于稳定状态时,弹簧的距离接近与他们的理想距离。KK算法的复杂度依然是N2,但是在收敛性方面得到了很大的提高。
Davidson和Harel提出的DH算法根据顶点分布、边界靠近,边长及边交叉等约束来建立系统的能量函数。调整约束的权重能量满足了不同的美学标准,而且他们使用了模拟退火算法(SA,Simulated Annealing)来求解能量函数的最小值。SA算法解得的结果非常接近能量最小点,并且他们在算法的最后阶段加入了针对边交叉及边点交叠的两个罚函数,使得该算法与其他算法相比能够产生效果更好的节点布局。但是比较耗时。
Fruchterman和Reingold基于再次改进的弹簧模型提出了FR算法。该算法主要遵循两个原则:有边连接的节点应该相互靠近;节点间不能离的太近。FR算法主要将无向图中的节点模拟成原子,通过模拟原子间的力场来计算节点间的位置关系。算法通过考虑原子间引力和斥力的互相作用,计算节点的速度和加速度。依照类似原子的运动规律,系统最终进入一种动态的平衡状态。FR算法还采用了网格变量方法进行了优化。将布点屈原分成若干网格,计算斥力的时候只考虑节点与相邻的网格的节点间的作用。若以K表示节点周围空白的区域的理想半径,d表示节点间的距离,则斥力计算公式为: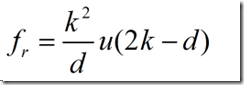 其中,
其中,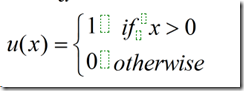
布点算法之Stress majorization
.stress majorization算法主要通过计算整个系统的总能量(Stress),Stress的定义如下 其中第二项为
其中第二项为
Stress(X)最小的时候X满足,![]() ,通常情况下,Stress最小的判断:
,通常情况下,Stress最小的判断:![]() ,迭代的deadline通常取值,10-4.
,迭代的deadline通常取值,10-4.
这个Stress majorization只对连通图有效,对于非连通图,需要自己处理。可以在最短路径矩阵中定义非连通图之间的最短路径。包括孤立点。





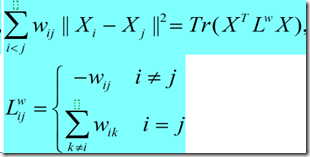
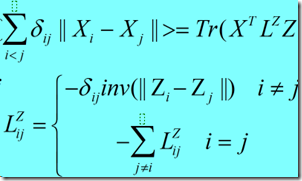
















 105
105

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








