动态规划中等题

最新推荐文章于 2025-08-06 14:41:27 发布

转载最新推荐文章于 2025-08-06 14:41:27 发布 · 107 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/chentingk/p/5990155.html

文章标签：

#数据结构与算法

再次回顾

　　　　动态规划的基本技巧，就是在最优子问题上求解总问题的解，并且是存在状态转移方程的，欲求d(i)必先求出d(i-1)+A[i]的值。二维的动态规划题目，大多都是d(i,j)在d(i-1,j)或者d(i,j-1)上求最优。

数塔问题

　　　　传送门：数塔问题

　　　　有一个数塔，第i行有i个数字，求从第一行到最后一行最大的行进路线。

　　　　分析：欲求d(i,j)的最大解，它只能从下方两个数进行求和，所以得到状态方程:d(i,j) = max{d(i+1,j) + A[i][j],d(i+1,j+1) + A[i][j]}

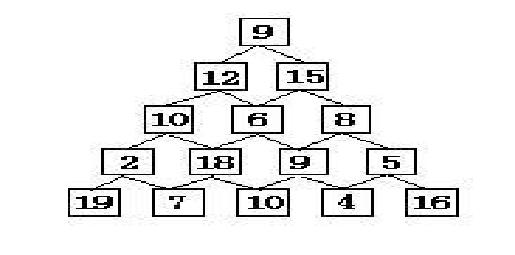
package DynamicProgramming;
/**
 * 数塔问题
 * 输入一个数塔，找到从根节点逐层找到最大的路径
 * @author MacBook
 *
 */
//i表示行
//j表示列
 
public class NumberTower {
    public static void main(String[] args) {
        int data1[][] ={
                {9,0,0,0,0},
                {12,15,0,0,0},
                {10,6,8,0,0},
                {2,18,9,5,0},
                {19,7,10,4,16}
        };
        int data2[][] ={
                {7,0,0,0,0},
                {3,8,0,0,0},
                {8,1,0,0,0},
                {2,7,4,4,0},
                {4,5,2,6,5}
        };
        new NumberTower().counting(data1, 5);
        new NumberTower().counting(data2, 5);
    }
    //    a[i][j]           -- d(i,j)
    //        /    \
    //    a[i+1][j]  a[i+1][j+1] -- d(i+1,j) , d(i+1,j+1)
    //状态转移方程：d(i-1,j) = max{d(i+1,j) + a[i][j] , d(i+1,j+1) + a[i][j]}
    public void counting(int[][] data,int rank){
        int [][] state = new int[data.length][data[0].length];
        for(int i = 0 ;i<rank;i++){
            state[rank-1][i]+=data[rank-1][i];
        }
        for(int i = rank -2;i>=0;i--){
            for(int j = 0;j<=i;j++){
                System.out.println("d = "+data[i][j]);
                System.out.println(state[i+1][j]+" "+state[i+1][j+1]);
                state[i][j] = Math.max(state[i+1][j] + data[i][j], state[i+1][j+1] + data[i][j]);
                System.out.println("result="+state[i][j]);
            }
        }
        System.out.println(state[0][0]);
    }
}

AvoidRoads

　　　　传送门：avoidroads

　　　　题目大致意思是，有一个height和width这么大的方格，每个坐标之间有一条道路，求从左下角到右上角可能行进的路线。其中可以输入从从哪个坐标到哪个坐标的道路不可通行；只能往右或者往上走。

　　　　首先我们考虑，当格子为一元的时候，即height=width=1的时候，并且(0,0),(1,0)无法通行。右上角只接受来自左边的可能性和来自右边的可能性。

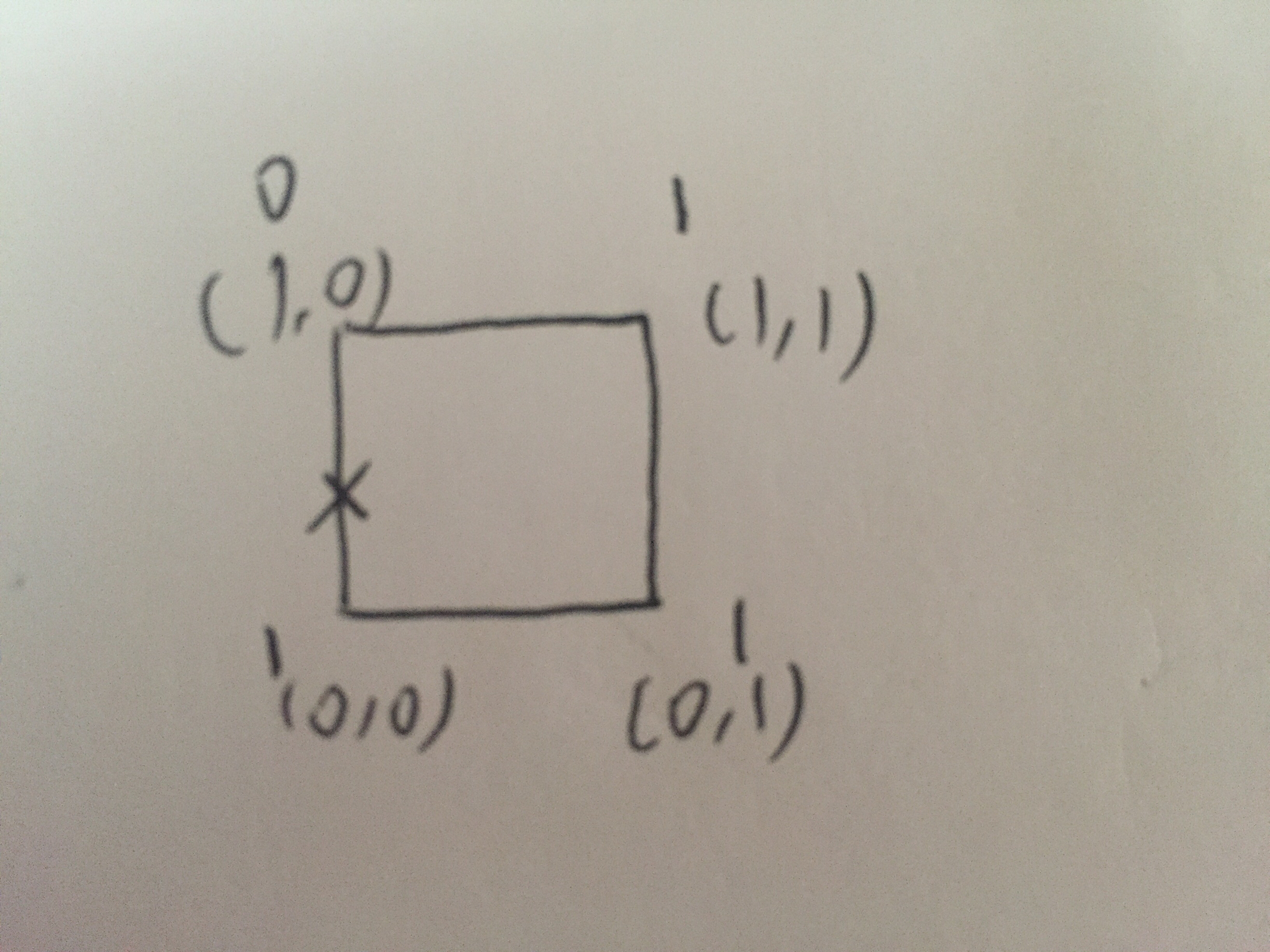
　　　　进而，我们考虑二元格子。

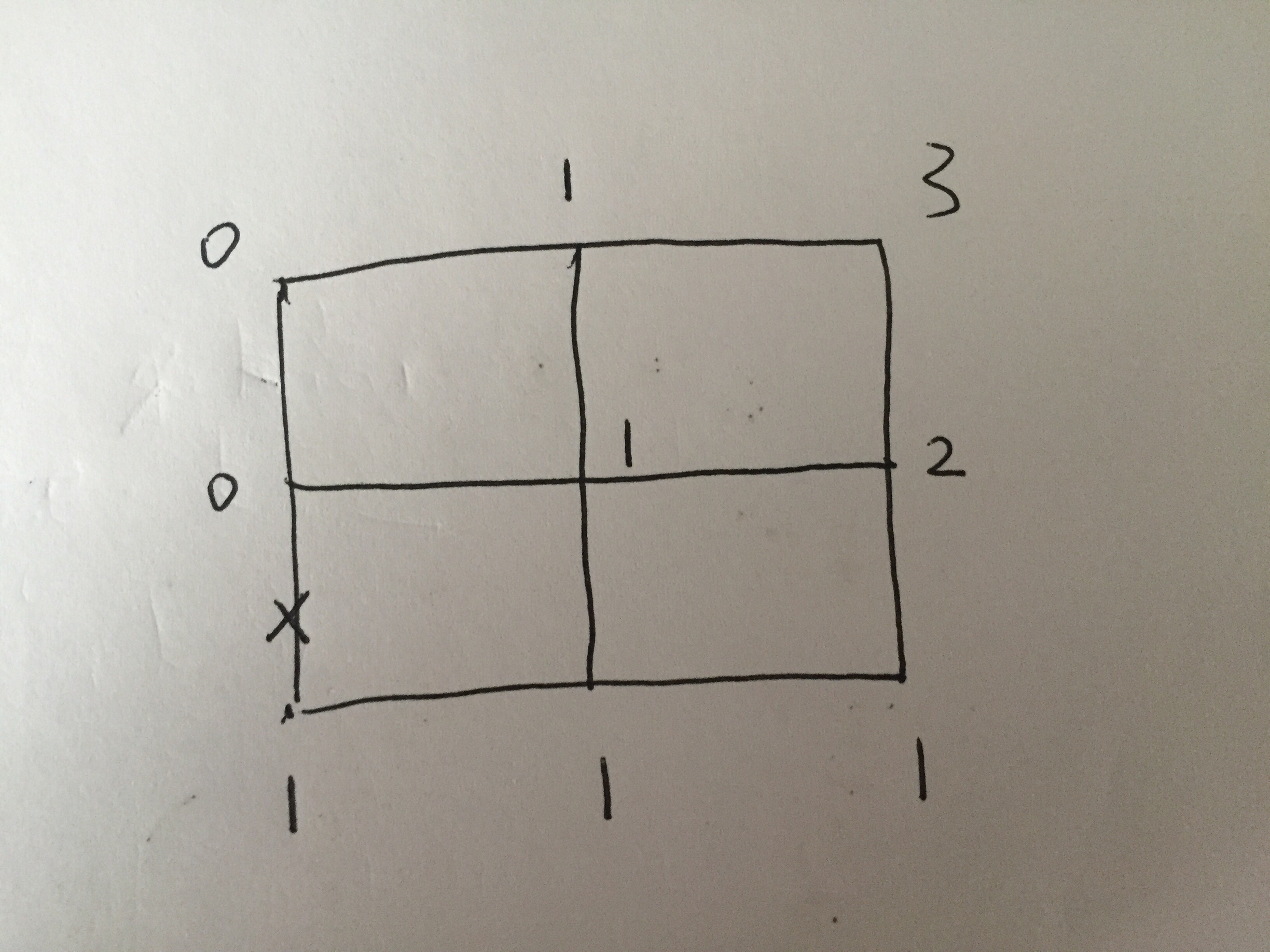
　　　　最后我们考虑状态转移方程，当height和width为i和j的时候，d(i,j) = d(i-1,j) + d(i,j-1) 并且无法通行的道路（从左边或者从下方）置零。

　　　　因为矩阵的对称性，从左上角到右下角的计算等价于从左下角到右上角的计算，所以我采用从左上角开始计算。

package DynamicProgramming;


/**
 * Problem Statement
 * Problem contains images. Plugin users can view them in the
 * applet.
 * 
 * In the city, roads are arranged in a grid pattern. Each point on the grid
 * represents a corner where two blocks meet. The points are connected by line
 * segments which represent the various street blocks. Using the cartesian
 * coordinate system, we can assign a pair of integers to each corner as shown
 * below.
 * 
 * You are standing at the corner with coordinates 0,0. Your destination is at
 * corner width,height. You will return the number of distinct paths that lead
 * to your destination. Each path must use exactly width+height blocks. In
 * addition, the city has declared certain street blocks untraversable. These
 * blocks may not be a part of any path. You will be given a String[] bad
 * describing which blocks are bad. If (quotes for clarity) "a b c d" is an
 * element of bad, it means the block from corner a,b to corner c,d is
 * untraversable. For example, let's say
 * 
 * Tips:
 *         输入街道的width，height，不可通行坐标data[][] 
 *         6 
 *         6 
 *         {"0 0 0 1",
 *         "6 6 5 6"}
 *         Returns: 252 Example from above
 *         数组表示x1y1 到 x2y2的道路不通；
 *         从左下角开始，到右上角为止，只能网上或者往右走；
 *         返回结果是求走法可能种类。
 * 分析：
 *         考虑一元格子，长度高度均为1的时候，从0，0到0，1不通，则0，0到0，1的路径可能性为1，因为从1，1来算，左边到达的路径为0，下方到达的路径为1
 *         考虑到二元格子，长度高度为2的时候，依旧，从0，0到0，1不通，到达2，2的路径条数是从左边2，1和从下方1，2的路径条数的和；2，1的可能数为1，而1，2的可能条数为2，则2，2的最终结果为3
 *         考虑到n*m格子，长度为n，高度为m，则d(n,m) = d(n-1,m) + d(n,m-1),并且在block点置零。
 * 
 */
public class AvoidRoads {
    public static void main(String[] args) {
        int[][] data = {{0,0,1,0},
                        {1,2,2,2},
                        {1,1,2,1}};
        new AvoidRoads().counting(2, 2, data);
    }
    //初始状态0,0 赋值1
    //当前状态i,j 只能接受上方和左方的和
    //如果向量(i-1,j)<->(i,j) (i,j-1)<->(i,j)不通,则减去该道路上的值
    public long counting(int width,int height,int[][] data){
        long[][] state = new long[height+1][width+1];
        state[0][0] = 1;
        for(int i=0;i<=height;i++)
            for(int j=0;j<=width;j++){
                if(j-1>=0)
                {
                    state[i][j] += state[i][j-1];
                }
                if(i-1>=0){
                    state[i][j] += state[i-1][j];
                }
                //检查block
                if(data != null)
                for(int k=0;k<data.length;k++){
                    //道路方向性
                    if((data[k][2] == i && data[k][3] == j
                            && data[k][0] == i && data[k][1] == j-1) || 
                            (data[k][2] == i && data[k][3] == j -1
                            && data[k][0] == i && data[k][1] == j))
                        state[i][j] -= state[i][j-1];
                    if((data[k][2] == i && data[k][3] == j
                            && data[k][0] == i-1 && data[k][1] == j) || (
                            data[k][2] == i-1 && data[k][3] == j
                            && data[k][0] == i && data[k][1] == j))
                        state[i][j] -= state[i-1][j];
                }
            }

        return state[height][width];
    }
}

苹果问题

　　　　有一个m*n个格子的空间，每个格子里面有a[i][j]个苹果，从左上角开始到右下角，能得到的最大苹果数，只能向右或者向下行进。

　　　　状态转移方程毫无疑问d(i,j) = max{d(i-1,j) + a[i][j],d(i,j-1) + a[i][j]}

package DynamicProgramming;

/**
 * 有m*n个格子放置苹果，每次行进只能往右和往下，计算一个能达到的最大的苹果数的路线
 * @author MacBook
 *
 */
public class AppleNumbers {
    public static void main(String[] args) {
        int[][] data = {
                {1,2,3},
                {3,8,6},
                {6,2,3}
        };
        new AppleNumbers().counting(data);
    }
    //状态转移方程:d(i,j) = max{d(i - 1,j) + a[i][j], d(i,j - 1) + a[i][j]}
    public void counting(int[][] data){
        int[][] state = new int[data.length][data[0].length];
        state[0][0] = data[0][0];//初始化
        for(int i=1;i<data[0].length;i++)
            state[0][i] = (data[0][i] + state[0][i-1]);
        for(int i=1;i<data.length;i++)
            state[i][0] = (data[i][0] + state[i-1][0]);
        for(int i=1;i<data.length;i++)
            for(int j=1;j<data[0].length;j++)
            {
                state[i][j] = Math.max(state[i-1][j] + data[i][j], state[i][j-1] + data[i][j]); 
            }
        System.out.println(state[data.length-1][data[0].length-1]);
        }
        
}

0-1背包问题

　　　　十分经典，特别难理解。

　　　　题目大意：有n件物品，它们各自的重量为w[i]，它们各自的价值为c[i]，背包的容量为m，求背包能放下的最大价值。

　　　　分析：我们需要一个函数，来控制这些变量以求最优解。既然有n件物品和m的容量，则我们使用f[i][j]来表示第i件物品的放入使得容量为j的背包的最大价值为几何？f[i][j]的值取决于在i-1件物品上的最优解是否放入第i件物品，也就是说状态转移方程为f[i][j] = max{f[i-1][j],f[i-1][j-w[i]] + c[i]}；它的意思就是，在当前状态，基于第i-1的最优解，放入背包和不放入背包的价值何者较大取何者。

　　　　　　　使用范例：有编号分别为a,b,c,d,e的五件物品，它们的重量分别是2,2,6,5,4，它们的价值分别是6,3,5,4,6，现在给你个承重为10的背包。

　　　　　　　n=5,m=10,w[i]={2,2,6,5,4},c[i]={6,3,5,4,6}。计算矩阵为：

　　　　　　　当i=2,j=4的时候，它考察i=1,j=4(即不放入第i件物品的时候）的价值与i=1,j=4-w[1]=2（即我放入第i件物品）较大者，显然6<9，此时背包放入了两件物品，a和b，所以最优解为9。

package DynamicProgramming;


/**
 * 0-1背包问题
 * 有n个物品，每个物品的重量w[i],每件物品的价值为c[i]
 * 给定一个背包容量为m
 * 如何能装下最大价值的物品
 * 令f(i,j)为状态函数，i表示放入前i件物品，j表示当前背包容量
 * f(i,j) = max{f(i-1,j),f(i-1,j-w[i]) + c[i]}
 * 当前最优解为放入前i-1件物品和放入当前物品的最大者
 * @author MacBook
 *
 */
public class Bags1 {
    public static void main(String[] args) {
        int[] w = {2,2,6,5,4};
        int[] c = {6,3,5,4,6};
        int contain = 10;
        new Bags1().counting(w, c, w.length, contain);
    }
    public void counting(int[] w,int[] c,int numbers,int contain){
        int[][] state = new int[numbers][contain];
        //初始化第一行s
        for(int j=0;j<contain;j++){
            if(j-w[0]>=0)
                state[0][j] += c[0];
        }
        for(int i=1;i<numbers;i++)
            for(int j=0;j<contain;j++){
                state[i][j] = state[i - 1][j];  
                if (j >= w[i])  
                {  
                    state[i][j] = Math.max(state[i - 1][j],state[i - 1][j - w[i]] + c[i]);  
                } 
            }
        for(int i=0;i<numbers;i++)
        {
            for(int j=0;j<contain;j++)
                System.out.print(state[i][j]+" ");
            System.out.println();
        }
    }
}