1.爬楼梯问题,到达楼梯的第i阶有多少中爬法
关键:第i阶楼梯,只可能从楼梯第i-1阶与i-2阶到达,所以到达第i阶的爬法与第i-1阶、第i-2阶的爬法直接相关。
这类问题分为四步:
1)原问题与子问题:找到子问题
2)第i个状态即为i阶台阶的所有走法数量
3)确认边界状态的值,边界状态为1阶台阶有一种走法,2阶有两种走法,即dp[1]=1,d[2]=2
4)确定状态转移方程dp[n] = dp[i-1] + dp[i-2]
代码实现:
public class Solution {
public int JumpFloor(int target) {
if(target<0)
return -1;
int[] dp = new int[target+2]; //每个数组里存的是有多少种方法
dp[1] = 1;
dp[2] = 2;
for(int i=3;i<=target;i++){
dp[i] = dp[i-1] + dp[i-2];
}
return dp[target];
}
}扩展:如果青蛙一次可以跳一阶,两阶,三阶,求到n阶台阶的跳法:
dp[n] = dp[n-1] + dp[n-2] + dp[n-3]
2.打家劫舍问题
一条直线上,有n个房屋,每个房屋中有数量不等的财宝,盗贼从房屋盗取财宝,如果从相邻的两个房屋盗取财宝就会触发报警器,问在不触发报警器的前提下,最多可以获取多少财宝。
记忆化搜索:
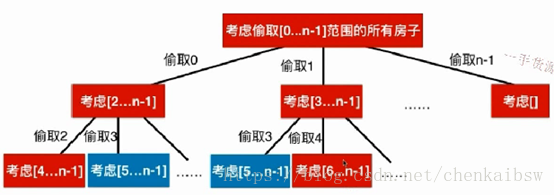
首先偷取了数组下标为0的房子,此时下一个房子就是从[2,n-1](因为不能偷取相邻的),可以理解题目是求从下标为0出开始偷取的最大值,如果先偷取了下标为0,那么转变为求从下标为2出开始偷取的最大值(递归下去),同理如果偷取的是第1个房子,此时下一个房子的偷取范围[3,n-1].........
从图中可以看到重叠子问题,所以可以使用记忆化搜索的方式。
代码实现(记忆化搜索方式):
class JianZhiOffer{
static int[] memo; //memo[i]表示抢劫nums[i...n]所能获得的最大收益。
public static void main(String[] args) {
int[] a = {5,2,6,3,1,7};
memo = new int[a.length];
Arrays.fill(memo,-1);
System.out.println(tryRob(a,0));
}
public static int tryRob(int[] nums,int index){
if(index>=nums.length) //这个条件???
return 0;
if(memo[index]!=-1)
return memo[index];
int temp = -1;
for(int i=index;i<nums.length;i++){
if(nums[i]+tryRob(nums,i+2)>temp)
temp = nums[i]+tryRob(nums,i+2);
memo[index] = temp;
}
return temp;
}
}if(index>=nums.length) //这个条件???
return 0;如果index = 3,此时temp = nums[3] + tryRob(nums,5);其实tryRob(nums,5) = 0
如果index = 4 ,此时temp = num[4] + tryRob(nums,6);其中tryRob(nums,6) = 0
memo[i]表示考虑抢劫nums[i...n]所能获得的最大收益关键:选择第i个房间盗取财宝,就一定不能选择第i-1个房间盗取财宝,若不选择第i个房间盗取财宝,则相当于只考虑前i-1个房间盗取财宝。
与上题的思路有一点一样:上题n级台阶有两种情况到达,第一种是从n-1台阶,另一个中是从n-2级台阶。
这题,盗取第n个房间的财宝,有两种方式,一种是从n-1房间,另一种是从n-2个房间
状态转移方程:dp[i] = max(dp[i-1],dp[i-2]+nums[i]);
代码实现:
class DP{
public static void main(String[] args){
int[] a = {5,2,6,3,1,7};
rob(a);
}
public static void rob(int nums[]){
int[] dp = new int[nums.length];
dp[0] = nums[0];
dp[1] = Math.max(nums[0], nums[1]);
for(int i=2;i<=nums.length-1;i++){
dp[i] = Math.max(dp[i-2]+nums[i],dp[i-1]);
}
System.out.println(dp[nums.length-1]);
}
}3.最大字段和
给定一个数组,求这个数组的连续子数组中,最大的那一段的和例如:{14,-2,4,-3,5,7,2,-39,22},和最大子序列是{14,-2,4,-3,5,7,2},返回27。
思路:求n个数的数组的最大子序列的和,转为分别求以第1个、第2个......第n个数字结尾的最大自序列和,在找出n个结果中的最大值。
dp[i]代表以第i个数字结尾的最大子段和,求dp[i]与dp[i-1]的关系。
代码实现:
//数组的所有连续子段的最大和
class DP
{
public static void main(String[] args)
{
int[] a = {14,-2,4,-3,5,7,2,-39,22};
maxSum(a,a.length);
}
public static void maxSum(int[] a,int n)
{
int[] dp = new int[a.length];
dp[0] = a[0];
for(int i=1;i<n;i++)
{
dp[i] = Math.max(dp[i-1]+a[i], a[i]);
}
//System.out.println(Arrays.toString(dp));
//取出dp数组中的最大值
int max = Integer.MIN_VALUE;
for(int i=0;i<dp.length;i++)
{
if(dp[i]>max)
max = dp[i];
}
System.out.println(max);
}
}4.剑指Offer(第二版)面试题14:剪绳子
题目一:给你一根长度为n的绳子,请把绳子剪成m段 (m和n都是整数,n>1并且m>1)每段绳子的长度记为k[0],k[1],...,k[m].请问k[0]*k[1]*...*k[m]可能的最大乘积是多少?
例如,当绳子的长度为8时,我们把它剪成长度分别为2,3,3的三段,此时得到的最大乘积是18.
分析:定义函数dp(n)为把长度为n的绳子剪成若干段后各段程度乘积的最大值。在剪第一刀的时候,我们有n-1中选择,也就是剪出来的第一段绳子的可能长度分别为1,2,.....;n-1,对应的第二段绳子的长度为n-1,n-2......1。因此 dp(n)=max(dp(i)*dp(n-i)),其中0<i<n。我们按照从下到上的顺序计算,也就是说我们先得到dp[(2)、dp(3)...然后求得dp(n),其中dp(n)是dp(1)*dp(n-1),dp(2)*dp(n-2).....dp(n-1)*dp(1)中的最大值。举例子说明:n=4时,dp[4]=dp[1]*dp[3],表示将长度为4的绳子,剪成1,3两段后的乘积,同样dp[2] = dp[2]*dp[2],表示将长度为4的绳子,减成2,2两段后的乘积。
代码实现:
//剪绳子问题
class JianZhiOffer{
public static void main(String[] args) {
System.out.println(maxCutting(8));
}
public static int maxCutting(int length){
if(length<=1) //如果小于等于1,输入不合法
return 0;
if(length==2) //可以分为1,1
return 1;
if(length==3) //可以分为:1,2 1,1,1
return 2;
int[] dp = new int[length+1]; //dp[n]计为长度为n的绳子剪开后的最大乘积
dp[0] = 0;
dp[1] = 1;
dp[2] = 2;
dp[3] = 3; //从dp[1]-dp[3]都包含了自己在内
for(int i=4;i<=length;i++){
int max = 0;
for(int j=1;j<=i/2;j++){
int temp = dp[j]*dp[i-j]; //长度为i的绳子的剪开后的最大的绳子等于它被剪开后子绳子的最大长度
if(temp>max)
max = temp;
}
dp[i] = max;
}
return dp[length];
}
}说明:从dp[1]到dp[3]都包含了自己在内,而从dp[4]开始是按照题意所求的值并且从4开始都是由1,2,3拼凑成的。
同样的问题有

5.给定一个m*n的方格,起始点为方格的最左上方,终点为方格的最右下方,一个机器人只能向下以及向右移动,需要求出机器人从起始点到终点一共有多少种不重复的路径。问题的输入为方格的长度m以及宽度n,输出为不同路径的数量。

https://blog.youkuaiyun.com/codekiller_/article/details/73008244https://blog.youkuaiyun.com/codekiller_/article/details/73008244
机器人只能经过方格上方或者方格左侧到达方格,dp[i][j] = dp[i-1][j] + dp[i][j-1],同时dp[0][j] = dp[i][0] = 0。
代码实现:
class DP{
public static void main(String[] args) {
int m = 3;
int n = 6;
int[][] dp = new int[m][n];
for(int i=0;i<m;i++){
for(int j=0;j<n;j++){
if(i==0||j==0){
dp[i][j] = 1;
}
else{
dp[i][j] = dp[i-1][j] + dp[i][j-1];
}
}
}
for(int i=0;i<m;i++){
for(int j=0;j<n;j++){
System.out.print(dp[i][j]+" ");
}
System.out.println();
}
System.out.println(dp[m-1][n-1]);
}
}同种类型的题:

https://blog.youkuaiyun.com/weixin_38314447/article/details/79074795
代码实现(动态规划的方法):
class DP{
public static void main(String[] args) {
int m = 9;
int n = 9;
int[][] dp = new int[9][9];
for(int i=0;i<9;i++){
for(int j=0;j<9;j++){
if(i==0||j==0){
dp[i][j] = 1;
}
else{
dp[i][j] = dp[i-1][j] + dp[i][j-1];
}
}
}
for(int i=0;i<9;i++){
for(int j=0;j<9;j++){
System.out.print(dp[i][j]+" ");
}
System.out.println();
}
System.out.println(dp[m-1][n-1]);
}
}DFS的方法实现:http://www.it610.com/article/5451938.htm

分析:在遇到grid[i][j] = 1的地方,dp[i][j] 设置为0
代码实现:
class DP{
public static void main(String[] args) {
int m = 3;
int n = 3;
int[][] grid = new int[m][n]; //格子中的数组
grid[1][1] = 1; //其中中间值为1
int[][] dp = new int[m][n];
for(int i=0;i<m;i++){
for(int j=0;j<n;j++){
if(i==0||j==0){
dp[i][j] = 1;
}
else if(grid[i][j]==0){
dp[i][j] = dp[i-1][j] + dp[i][j-1];
}
}
}//打印看一下dp矩阵
for(int i=0;i<m;i++){
for(int j=0;j<n;j++){
System.out.print(dp[i][j]+" ");
}
System.out.println();
}
System.out.println(dp[m-1][n-1]);
}
}1 1 1
1 0 1
1 1 2
2在[1,1]位置,dp[1][1]设为0.
6.完美平方数问题

























 316
316

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








