Problem:
Given a non-negative integer num, repeatedly add all its digits until the result has only one digit.
For example:
Given num = 38, the process is like: 3 + 8 = 11, 1 + 1 = 2. Since 2 has only one digit, return it.
Could you do it without any loop/recursion in O(1) runtime?
Summary:
给出一个整型数,反复求出它各个位数之和,直至和小于10。
能否不使用循环和递归,复杂度为O(1)。
Analysis:
1、常规方法:
1 class Solution { 2 public: 3 int addDigits(int num) { 4 while (num > 9) { 5 int res = 0; 6 while (num) { 7 res += num % 10; 8 num /= 10; 9 } 10 11 num = res; 12 } 13 14 return num; 15 } 16 };
2、Hint提示:Digital Root (https://en.wikipedia.org/wiki/Digital_root)
Digital roots can be calculated with congruences in modular arithmetic rather than by adding up all the digits, a procedure that can save time in the case of very large numbers.
It helps to see the digital root of a positive integer as the position it holds with respect to the largest multiple of 9 less than the number itself. For example, the digital root of 11 is 2, which means that 11 is the second number after 9. Likewise, the digital root of 2035 is 1, which means that 2035 − 1 is a multiple of 9. If a number produces a digital root of exactly 9, then the number is a multiple of 9.
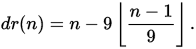
The formula is:
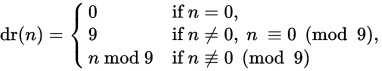 or
or 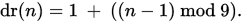
1 class Solution { 2 public: 3 int addDigits(int num) { 4 if (num <= 9) { 5 return num; 6 } 7 else if (num % 9 == 0) { 8 return 9; 9 } 10 else { 11 return num % 9; 12 } 13 } 14 };
or
1 class Solution { 2 public: 3 int addDigits(int num) { 4 return 1 + ((num - 1) % 9); 5 } 6 };







 本文介绍了一种快速计算数字根的方法,即反复将一个非负整数的各位数字相加直至结果仅剩一位数字的过程。文章提供了两种解决方案:一种是通过循环逐位累加的方式;另一种则是利用数字根的概念,采用取模运算实现O(1)的时间复杂度,避免了循环和递归,极大地提高了计算效率。
本文介绍了一种快速计算数字根的方法,即反复将一个非负整数的各位数字相加直至结果仅剩一位数字的过程。文章提供了两种解决方案:一种是通过循环逐位累加的方式;另一种则是利用数字根的概念,采用取模运算实现O(1)的时间复杂度,避免了循环和递归,极大地提高了计算效率。
















 1204
1204

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








