Codeforces Round #460 (Div. 2)

A. Supermarket

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

We often go to supermarkets to buy some fruits or vegetables, and on the tag there prints the price for a kilo. But in some supermarkets, when asked how much the items are, the clerk will say that a yuan for b kilos (You don't need to care about what "yuan" is), the same as a / b yuan for a kilo.

Now imagine you'd like to buy m kilos of apples. You've asked n supermarkets and got the prices. Find the minimum cost for those apples.

You can assume that there are enough apples in all supermarkets.

Input

The first line contains two positive integers n and m (1 ≤ n ≤ 5 000, 1 ≤ m ≤ 100), denoting that there are n supermarkets and you want to buy m kilos of apples.

The following n lines describe the information of the supermarkets. Each line contains two positive integers a, b (1 ≤ a, b ≤ 100), denoting that in this supermarket, you are supposed to pay a yuan for b kilos of apples.

Output

The only line, denoting the minimum cost for m kilos of apples. Please make sure that the absolute or relative error between your answer and the correct answer won't exceed 10 - 6.

Formally, let your answer be x, and the jury's answer be y. Your answer is considered correct if .

Examples

input

3 5
1 2
3 4
1 3

output

1.66666667

input

2 1
99 100
98 99

output

0.98989899

Note

In the first sample, you are supposed to buy 5 kilos of apples in supermarket 3. The cost is 5 / 3 yuan.

In the second sample, you are supposed to buy 1 kilo of apples in supermarket 2. The cost is 98 / 99 yuan.

 

 知道每个物品单价，求出最小的应付总额

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int main()
{
    int n,m;
    cin>>n>>m;
    double mi=1e9;
    for(int i=0,x,y;i<n;i++)
    {
        cin>>x>>y;
        mi=min(mi,m*x*1.0/y);
    }
    printf("%12f",mi);
    return 0;
}

B. Perfect Number

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

We consider a positive integer perfect, if and only if the sum of its digits is exactly 10. Given a positive integer k, your task is to find the k-th smallest perfect positive integer.

Input

A single line with a positive integer k (1 ≤ k ≤ 10 000).

Output

A single number, denoting the k-th smallest perfect integer.

Examples

input

1

output

19

input

2

output

28

Note

The first perfect integer is 19 and the second one is 28.

 

 本来以为是这个数加上这个数所有位数的和和10的差，我这样是读错题了，不是得到的和是10的倍数，而是和为10

其实是个暴力

大暴力做法，这个还是优化了些，dfs更快些，i=19，每次+9可以优化些常数

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int la(int n)
{
    int s=0;
    while(n)
    {
        s+=n%10;
        n/=10;
    }
    return s;
}
int main()
{
    int n;
    cin>>n;
    int cnt=0;
    for(int i=1;;i++)
    {
        if(la(i)==10)
        {
            cnt++;
            if(cnt==n)
            {
                cout<<i;
                break;
            }
        }
    }
    return 0;
}

C. Seat Arrangements

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Suppose that you are in a campus and have to go for classes day by day. As you may see, when you hurry to a classroom, you surprisingly find that many seats there are already occupied. Today you and your friends went for class, and found out that some of the seats were occupied.

The classroom contains n rows of seats and there are m seats in each row. Then the classroom can be represented as an n × m matrix. The character '.' represents an empty seat, while '*' means that the seat is occupied. You need to find k consecutive empty seats in the same row or column and arrange those seats for you and your friends. Your task is to find the number of ways to arrange the seats. Two ways are considered different if sets of places that students occupy differs.

Input

The first line contains three positive integers n, m, k (1 ≤ n, m, k ≤ 2 000), where n, m represent the sizes of the classroom and k is the number of consecutive seats you need to find.

Each of the next n lines contains m characters '.' or '*'. They form a matrix representing the classroom, '.' denotes an empty seat, and '*' denotes an occupied seat.

Output

A single number, denoting the number of ways to find k empty seats in the same row or column.

Examples

input

2 3 2
**.
...

output

3

input

1 2 2
..

output

1

input

3 3 4
.*.
*.*
.*.

output

0

Note

In the first sample, there are three ways to arrange those seats. You can take the following seats for your arrangement.

• (1, 3), (2, 3)
• (2, 2), (2, 3)
• (2, 1), (2, 2)

 C就是让你在某行某列找到两个连续的k个位置，上下扫一下就行，但是k==1是特殊的

#include<bits/stdc++.h>
using namespace std;
string s[2005];
int main()
{
    ios::sync_with_stdio(false);
    int n,m,k;
    cin>>n>>m>>k;
    for(int i=0; i<n; i++)
        cin>>s[i];
    int sum=0;
    for(int i=0; i<n; i++)
    {
        int t=0;
        for(int j=0; j<m; j++)
        {

            if(s[i][j]=='.')t++;
            else
            {
                if(t>=k)sum+=t-k+1;
                t=0;
            }
        }
        if(t>=k)sum+=t-k+1;
    }
    if(k!=1)
    {
        for(int i=0; i<m; i++)
        {
            int t=0;
            for(int j=0; j<n; j++)
            {
                if(s[j][i]=='.')t++;
                else
                {
                    if(t>=k)
                        sum+=t-k+1;
                    t=0;
                }
            }
            if(t>=k)sum+=t-k+1;
        }
    }
    cout<<sum;
    return 0;
}

 

D. Substring

time limit per test

3 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given a graph with n nodes and m directed edges. One lowercase letter is assigned to each node. We define a path's value as the number of the most frequently occurring letter. For example, if letters on a path are "abaca", then the value of that path is 3. Your task is find a path whose value is the largest.

Input

The first line contains two positive integers n, m (1 ≤ n, m ≤ 300 000), denoting that the graph has n nodes and m directed edges.

The second line contains a string s with only lowercase English letters. The i-th character is the letter assigned to the i-th node.

Then m lines follow. Each line contains two integers x, y (1 ≤ x, y ≤ n), describing a directed edge from x to y. Note that x can be equal to y and there can be multiple edges between x and y. Also the graph can be not connected.

Output

Output a single line with a single integer denoting the largest value. If the value can be arbitrarily large, output -1 instead.

Examples

input

5 4
abaca
1 2
1 3
3 4
4 5

output

3

input

6 6
xzyabc
1 2
3 1
2 3
5 4
4 3
6 4

output

-1

input

10 14
xzyzyzyzqx
1 2
2 4
3 5
4 5
2 6
6 8
6 5
2 10
3 9
10 9
4 6
1 10
2 8
3 7

output

4

Note

In the first sample, the path with largest value is 1 → 3 → 4 → 5. The value is 3 because the letter 'a' appears 3 times.

 

 拓扑排序+dp

#include<bits/stdc++.h>
using namespace std;
const int N=3e5+5;
int n,m,k,ans,d[N],have[N][27],vis[N];
vector<int> G[N];
queue<int> Q;
string a;
int main()
{
    ios::sync_with_stdio(false);
    cin>>n>>m>>a;
    for(int i=0,u,v; i<m; i++)
        cin>>u>>v,G[u].push_back(v),d[v]++;
    for(int i=1; i<=n; i++) if(!d[i]) Q.push(i);
    while (Q.size())
    {
        int u=Q.front();
        Q.pop();
        have[u][a[u-1]-'a']++;
        vis[u]=1;
        for(int i=0; i<26; i++) 
            ans=max(ans,have[u][i]);
        for (int v:G[u])
        {
            for(int i=0; i<26; i++) have[v][i]=max(have[v][i],have[u][i]);
            d[v]--;
            if(!d[v]) Q.push(v);
        }
    }
    for(int i=1; i<=n; i++) 
        if(!vis[i]) return 0*puts("-1");
    printf("%d",ans);
}

 

E. Congruence Equation

time limit per test

3 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Given an integer x. Your task is to find out how many positive integers n (1 ≤ n ≤ x) satisfy

where a, b, p are all known constants.

Input

The only line contains four integers a, b, p, x (2 ≤ p ≤ 106 + 3, 1 ≤ a, b < p, 1 ≤ x ≤ 1012). It is guaranteed that p is a prime.

Output

Print a single integer: the number of possible answers n.

Examples

input

2 3 5 8

output

2

input

4 6 7 13

output

1

input

233 233 10007 1

output

1

Note

In the first sample, we can see that n = 2 and n = 8 are possible answers.

 

 数论题，要找循环节的

Trying all integers from 1 to x is too slow to solve this problem. So we need to find out some features of that given equation.

Because we have 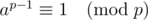 when p is a prime, it is obvious that  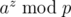falls into a loop and the looping section is p - 1. Also,  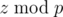has a looping section p. We can try to list a chart. (In the chart shown below, n is equal to i·(p - 1) + j)

We can see that n·an has a looping section p(p - 1).

Therefore, we can enumerate j from 1 to p - 1 and calculate b·a - j. Let's say the result is y, then we have 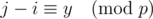 (You can refer to the chart shown above to see if it is). So for a certain j, the possible i can only be (j - y), p + (j - y), ..., p·t + (j - y). Then we can calculate how many possible answers n in this situation (i.e. decide the minimum and maximum possible t using the given lower bound 1 and upper bound x). Finally we add them together and get the answer.

找p-1就可以了

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll x,ans,P,a,b,p,t,k;
ll bin(ll a,ll b)
{
    ll ans=1;
    while(b)
    {
        if(b&1)ans=ans*a%p;
        a=a*a%p;
        b>>=1;
    }
    return ans;
}
int main()
{
    cin>>a>>b>>p>>x;
    P=p*(p-1);
    for(int j=1; j<p; j++)
    {
        t=b*bin(a,p-j-1)%p,k=(p*j%P+(p-t)*(p-1)%P)%P;
        ans+=x/P;
        if(x%P>=k)ans++;
    }
    cout<<ans;
}

另一份熟练的代码

 #include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll a,b,p,x;
int main()
{
    cin>>a>>b>>p>>x;
    ll ans=0,r=b,t,t1;
    for(int i=p-1;i;i--)
    {
        if(i<=x)
        {
            t=(i-r+p)%p,t1=(x-i)/(p-1);
            ans+=t1/p+(t1%p>=t);
        }
        r=r*a%p;
    }
    cout<<ans;
}

 

转载于:https://www.cnblogs.com/BobHuang/p/8398371.html