霍夫曼编码详解-优快云博客

2019独角兽企业重金招聘Python工程师标准>>>

声明

本文主要参考了WIKI百科和算法导论，对huffman算法做一总结，本文将重点放在huffman表的证明以及具体实现上。

简介

霍夫曼编码（Huffman Coding）是一种编码方式，是一种用于无损数据压缩的熵编码（权编码）演算法。也称“哈夫曼编码”，“赫夫曼编码”。1952年，David A. Huffman在麻省理工攻读博士时所发明的，并发表于《一种构建极小多余编码的方法》（A Method for the Construction of Minimum-Redundancy Codes）一文。

在计算机资料处理中，霍夫曼编码使用变长编码表对源符号（如文件中的一个字母）进行编码，其中变长编码表是通过一种评估来源符号出现机率的方法得到的，出现机率高的字母使用较短的编码，反之出现机率低的则使用较长的编码，这便使编码之后的字符串的平均长度、期望值降低，从而达到无损压缩数据的目的。

例如，在英文中，e的出现机率最高，而z的出现概率则最低。当利用霍夫曼编码对一篇英文进行压缩时，e极有可能用一个位元来表示，而z则可能花去25个位元（不是26）。用普通的表示方法时，每个英文字母均占用一个字节（byte），即8个位元。二者相比，e使用了一般编码的1/8的长度，z则使用了3倍多。倘若我们能实现对于英文中各个字母出现概率的较准确的估算，就可以大幅度提高无损压缩的比例。

霍夫曼树又称最优二叉树，是一种带权路径长度最短的二叉树。所谓树的带权路径长度，就是树中所有的叶结点的权值乘上其到根结点的路径长度（若根结点为0层，叶结点到根结点的路径长度为叶结点的层数）。树的路径长度是从树根到每一结点的路径长度之和，记为WPL=（W1*L1+W2*L2+W3*L3+...+Wn*Ln），N个权值Wi（i=1,2,...n）构成一棵有N个叶结点的二叉树，相应的叶结点的路径长度为Li（i=1,2,...n）。可以证明霍夫曼树的WPL是最小的。

伪代码

1.我们假设C存放了所有的关键字对象key， key.fre 表示该关键字出现的频率，key.ch 使该关键字的符号
2.Q是一个存放node的最小优先队列，node是一个辅助结构，node.fre记录了其下面所有叶子，即key的fre和.Q是一个以fre为关键字的最小优先队列 
3.初始状态每一个key作为一个叶子关联一个node存放在Q中 
HUFFMAN(C)
Q = C; 
while Q.size() > 1 
       do
          z->new node;  
          z.lft -> node x -> pop one from Q;
          z.rht -> node y -> pop one from Q;
          z.fre -> x.fre + y.fre; 
          push z into Q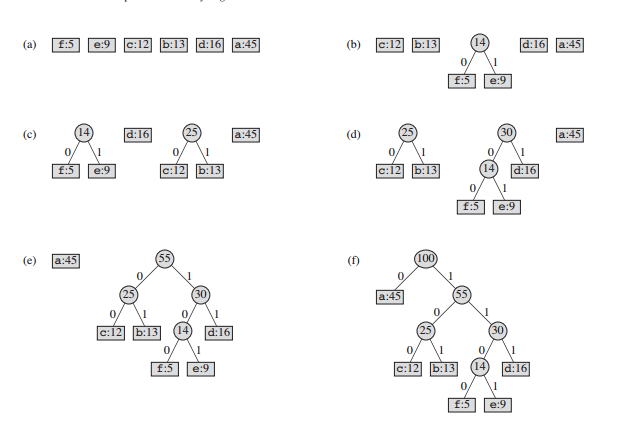

具体实现

代码一

/**
 * @brief code for tp
 * @author xiyan
 * @date 2014/06/20
 *
 */
#include <iostream>
#define EOF -1
using namespace std;
class huffman_node;
class huffman;
class huffman_node{
public:
        huffman_node(const int &val, const int &power):val(val), power(power), lft(NULL), rht(NULL), next(NULL){}
        int val;
        int power;
        huffman_node *lft;
        huffman_node *rht;
        huffman_node *next;
};
class huffman
{
public:
        huffman():huffman_head(new huffman_node(EOF, 0)){}
        void add_new(huffman_node *new_node);
        void construct();
        int get_power(){
                huffman_node  *node = huffman_head->next;
                return huffman_power(node, 1);
        }
        void get_code(){
                huffman_node *node = huffman_head->next;
                return huffman_code(node, "huffman:");
        }
        void destory(){
            huffman_destory(huffman_head);
        }
        int huffman_power(huffman_node *node, int level);
        void huffman_code(huffman_node *node, string code);
        void huffman_destory(huffman_node *node);
        huffman_node *huffman_head;
};

void huffman::add_new(huffman_node *new_node)
{
        huffman_node *index = huffman_head;
        while(index->next && index->next->power < new_node->power){
                    index = index->next;
        }
        new_node->next = index->next;
        index->next = new_node;
}
void huffman::construct(){
    while(huffman_head->next){
            if(NULL == huffman_head->next->next)
                    return;
             huffman_node *new_node = new huffman_node(EOF,huffman_head->next->power + huffman_head->next->next->power);
             new_node->lft = huffman_head->next;
             new_node->rht = huffman_head->next->next;
             huffman_head->next  = new_node->rht->next;
             add_new(new_node);
    }
}
int huffman::huffman_power(huffman_node *node, int level){
    if(NULL == node) return 0;
    if(NULL == node->lft && NULL == node->rht) return node->power *level;
    return huffman_power(node->lft, level + 1) + huffman_power(node->rht, level + 1);
}

void huffman::huffman_code(huffman_node *node, string code)
{
    if(NULL == node->lft && NULL == node->rht){
            cout << "char:" << static_cast<char>(node->val) << " code:" << code << "\n";
            return;
    }
    string tmp;
    tmp = code;
    if(node->lft){
            tmp += '0';
            huffman_code(node->lft, tmp);
    }
    tmp = code;
    if(node->rht){
            tmp += '1';
            huffman_code(node->rht, tmp);
    }
}
void  huffman::huffman_destory(huffman_node *node)
{
    if(node->lft)
        huffman_destory(node->lft);
    if(node->rht)
        huffman_destory(node->rht);
    if(0 == node->lft  && 0 == node->rht){
        delete node;
        return;
    }
}

int main()
{
    char val;
    int power;
    huffman test;
    while(cin >> val >> power){
            cout << "val = "<< val << endl;
            cout << "power= " << power << endl;
            test.add_new(new huffman_node(val, power));
    }
    cout << "start construct" << endl;
            test.construct();
    cout << "huffman_power:"  << test.get_power() << endl;
    cout << "huffman_code:\n" ;  test.get_code();
    test.destory();
    return 0;
}

代码二

Copy from wike
//僅用於示範如何根據權值構建霍夫曼樹，
//沒有經過性能上的優化及加上完善的異常處理。
#include <cstdlib>
#include <iostream>
#include <deque>
#include <algorithm>
using namespace std;
const int size=10;
struct node                                 //霍夫曼樹節點結構
{
    unsigned key;                           //保存權值
    node* lchild;                           //左孩子指針
    node* rchild;                           //右孩子指針
};
deque<node*> forest;
deque<bool> code;                           //此處也可使用bitset
node* ptr;
int frequency[size]={0};
void printCode(deque<bool> ptr);            //用於輸出霍夫曼編碼
bool compare( node* a, node* b)
{
return a->key < b->key;
}
int main(int argc, char *argv[])
{
    for(int i=0;i<size;i++)
    {
        cin>>frequency[i];                  //輸入10個權值
        ptr=new node;
        ptr->key=frequency[i];
        ptr->lchild=NULL;
        ptr->rchild=NULL;
        forest.push_back(ptr);
    }//形成森林，森林中的每一棵樹都是一個節點
    //從森林構建霍夫曼樹
    for(int i=0;i<size-1;i++)
    {
  sort(forest.begin(),forest.end(),compare);
  ptr=new node;
                //以下代碼使用下標索引隊列元素，具有潛在危險，使用時請注意
  ptr->key=forest[0]->key+forest[1]->key;
  ptr->lchild=forest[0];
  ptr->rchild=forest[1];
  forest.pop_front();
  forest.pop_front();
  forest.push_back(ptr);
 }
    ptr=forest.front();//ptr是一個指向根的指針
    system("PAUSE");
    return EXIT_SUCCESS;
}
void printCode(deque<bool> ptr)
{
 //deque<bool>
 for (int i=0;i<ptr.size();i++)
 {
  if(ptr[i])
   cout<<"1";
  else
   cout<<"0";
 }
}