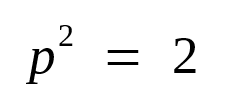本文通过两种方法证明了√2是一个无理数：一是高中数学中的反证法，二是利用微积分中的极限概念。首先，通过设定有理数p=m/n的形式，并通过推导得出矛盾，从而证明了不存在这样的有理数p；其次，借助极限的概念，通过对p的不同取值范围进行讨论，同样得到了不存在有理数p使得p²=2的结论。
证明：
今天看了一下数学分析方法来充实数学功底。话不多说，先写完。
记得在上高中的时候证明过这个，现将高中方法附上：
利用反证法，如果存在这样一个有理数p能满足题意。同时我们都得知，有理数可以写成分子/分母的形式。则可以把p改写为m/n，在这里没有一定保证m，n同为偶数，也就是两个数类型不定。则转化为后（m/n ）^2=2 -> m^2=2n^2。
由这个式子可知，m的平方必为偶数，因为（1）等式右边有个2（2）偶数的平方为偶数。如果m为偶数，m可被2整除，那么m的平方可被4整除，那么n的平方为偶数，那么n也为偶数。如果需要证明的等式成立，那么我们由任意m，n的奇偶来得到m，n都只能为偶数的情况。这显然与推论不符合。故不存在符合题意的p。
在这个问题中，可以采取大学学的微积分。我们知道，极限存在的条件为左右极限存在且相等。那我们可以试一下此证明。（如果左右极限不存在，也就说明没有极限喽）
假设在（1）p^2<2时，没有最大值。在（2）p^2>2时，没有最小值。
用数学语言来讲嘛，就是（1）对于每一个p，都存在一个q，使得p<q（2）对于每一个p，都存在一个q，使得p>q
如何来构造这个特殊的等式呢？这一点真的不明觉厉。
① q = p - ((p^2-2)/(p+2))，为什么要这样构造呢，一方面我们是为了得到p和q的大小的关系，另一方面我们得添加一个正负就在那一刹那的书，p^2-2，为什么分母为p+2呢，，恕我现在还不能解释。
对①变形，得(2p+2)/(p+2) = q，在对其进行变形得②q-2 = 2(p^2 - 2)/(p+2)^2
对（1）来说，由①得，q>p，由②得，q<2
对（2）来说，由②得，q<p，由②得，q>2
因此，（1）成立，（2）成立。得知（1）没有上界，（2）没有下届。综上所述，所以不存在有理数p使得p^2=2
小小感悟，数学公式打着真不方便，，排版也是个问题，等起来再说。赶紧睡觉，保持好习惯。
扫一扫
2420
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
