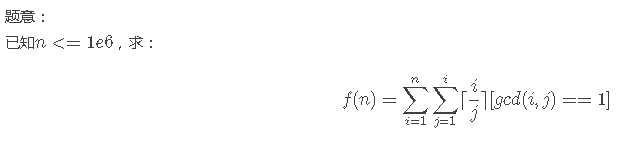
【数论】【莫比乌斯反演】【线性筛】hdu6134 Battlestation Operational-优快云博客

本文提供了一道涉及线性筛与数论转换的题目解答，通过使用莫比乌斯函数和线性筛算法求解特定数学问题。文中详细介绍了算法实现步骤，包括线性筛莫比乌斯函数、求约数个数等关键环节。

看这个题解吧：http://blog.youkuaiyun.com/wubaizhe/article/details/77338332

代码里顺便把几个常用的线性筛附上了。

Key：1、gcd(i,j)==1利用莫比乌斯函数的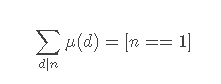性质进行转化。

2、变换求和符号的顺序。

3、发现，该式可以递推。

4、线性筛约数个数函数。

#include<cstdio>
#include<algorithm>
using namespace std;
#define MOD 1000000007
#define N 1000000
bool notpri[N+5];
int pri[N+5],n,mu[N+5],sum[N+5];
typedef long long ll;
void shai_mu()//线性筛莫比乌斯函数，并处理出前缀和
{
    notpri[1]=1; mu[1]=1;
    for(int i=2;i<=N;i++){
        if(!notpri[i]){
            pri[++pri[0]]=i;
            mu[i]=-1;
        }
        for(int j=1;j<=pri[0] && (ll)i*(ll)pri[j]<=(ll)N;j++){
            notpri[i*pri[j]]=1;
            mu[i*pri[j]]=-mu[i];
            if(i%pri[j]==0){
                mu[i*pri[j]]=0;
                break;
            }
        }
    }
    sum[1]=mu[1];
    for(int i=2;i<=N;i++){
        sum[i]=sum[i-1]+mu[i];
    }
}
int ysgs[N+5],facnum[N+5],d[N+5]/*d(i)是辅助数组，记录每个数的最小质因子的幂次*/;
void shai_facnum()//线性筛每个数的约数个数
{
	facnum[1]=1;
	for(int i=2;i<=N;++i){
		if(!notpri[i]){
			facnum[i]=2;
			d[i]=1;
		}
		for(int j=1;j<=pri[0] && (ll)i*(ll)pri[j]<=(ll)N;++j){
			if(i%pri[j]==0){
				facnum[i*pri[j]]=facnum[i]/(d[i]+1)*(d[i]+2);
				d[i*pri[j]]=d[i]+1;
				break;
			}
			facnum[i*pri[j]]=facnum[i]*2;
			d[i*pri[j]]=1;
		}
	}
}
int g[N+5];
int main(){
	//freopen("hdu6134.in","r",stdin);
	shai_mu();
	shai_facnum();
	g[1]=1;
	for(int i=2;i<=N;++i){
		g[i]=(g[i-1]+(facnum[i-1]+1))%MOD;
	}
	for(int i=2;i<=N;++i){
		g[i]=(g[i]+g[i-1])%MOD;
	}
	while(scanf("%d",&n)!=EOF){
		int ans=0;
		for(int i=1;i<=n;){
			ans=(ans+(int)((((ll)(sum[n/(n/i)]-sum[i-1]+(ll)MOD)%(ll)MOD)*(ll)g[n/i])%(ll)MOD))%MOD;
			i=n/(n/i)+1;
		}
		printf("%d\n",ans);
	}
	return 0;
}
/*
线性筛欧拉函数 
void get_eular()    
{    
    pnum = 0;  
    for(int i = 2; i < MAX; i++)    
    {    
        if(!noprime[i])    
        {    
            p[pnum ++] = i;    
            phi[i] = i - 1;    
        }    
        for(int j = 0; j < pnum && i * p[j] < MAX; j++)    
        {    
            noprime[i * p[j]] = true;    
            if(i % p[j] == 0)    
            {    
                phi[i * p[j]] = phi[i] * p[j];    
                break;    
            }    
            phi[i * p[j]] = phi[i] * (p[j] - 1);    
        }    
    }    
}   
*/

转载于:https://www.cnblogs.com/autsky-jadek/p/7491730.html