《计算机视觉：模型、学习和推理》——3.2 贝塔分布

本节书摘来自华章计算机《计算机视觉：模型、学习和推理》一书中的第3章，第3.2节,作者：（英）普林斯（Prince，J. D.）著， 更多章节内容可以访问云栖社区“华章计算机”公众号查看。

3.2　贝塔分布

贝塔分布（图3-2）是由单变量λ定义的连续分布，这里λ=[0,1]。因此，它适合表示伯努利分布中参数λ的不确定性。
如图3-2所示，贝塔分布有两个参数(α,β)∈［0，∞］，两个参数均取正值并且都影响曲线的形状。在数学上，贝塔分布的形式如下：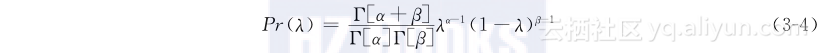

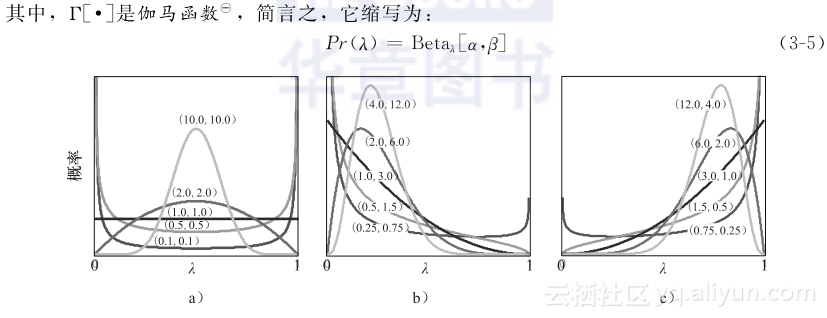
图3-2　贝塔分布。贝塔分布值域在[0,1]之间，有参数(α,β)，参数相对值决定预期值，所以E［λ］=α/(α+β)（括号内的数值显示每条曲线中的α、β）。随着(α,β)绝对值的增加，E［λ］两侧的分布更加集中，a）每条曲线中，E［λ］=0.5，分布的集中程度不同。b）E［λ］=0.25。c）E［λ］=0.75