JZOJ.3777【NOI2015模拟8.17】最短路（shortest）

Description

       小Y最近学得了最短路算法，一直想找个机会好好练习一下。话虽这么说，OJ上最短路的题目都被他刷光了。正巧他的好朋友小A正在研究一类奇怪的图，他也想凑上去求下它的最短路。

       小A研究的图可以这么看：在一个二维平面上有任意点(x,y)（0<=x<=N,0<=y<=M,且x,y均为整数），且(x,y)向(x-1,y)（必须满足1<=x）和(x,y-1)（必须满足1<=y）连一条边权为0的双向边。

       每个点都有一个非负点权，不妨设(x,y)的权值为F[x][y]，则有：

       1.x=0或y=0：F[x][y]=1；2.其他情况：F[x][y]=F[x-1][y]+F[x][y-1]。

       现在，小Y想知道(0,0)到(N,M)的最短路，即使得经过的点的权值之和最小。为了炫耀自己学过最短路算法，他决定和你进行一场比赛，看谁的程序跑得快。然则小Y没有学过高精度算法，所以他希望输出答案时只输出答案模1000000007后的值。

 

Input

       一行两个正整数N,M，表示图的大小。

Output

       一行一个整数Ans，表示答案模1000000007后的值。

 

Sample Input

1 2

Sample Output

6

 

Data Constraint

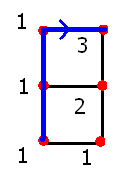见左图。

 

Hint

10%的数据满足N,M<=20；

30%的数据满足N,M<=100；

60%的数据满足min(N,M)<=100；

100%的数据满足N*M<=10^12。

 容易发现这其实是杨辉三角的一部分，最短路其实是确定的，沿这个矩形外围的一圈走，且一开始往较长的那一边走。

那么答案就是$m+1+\sum _{i=1}^{n}C_{m+i}^{i}$

我们容易发现$C_{m+i}^{i}\times \dfrac {m+i+1} {i+1}=C_{m+i+1}^{i+1}$

也就是上一个C值可以直接推到下一个C值，mod的是一个大质数，逆元一下就可以了。   （费马小定理）

$\dfrac {a} {b}=a\ast b^{p-2}\left( modP\right)$

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<cstdlib>
 4 #include<cmath>
 5 #define qaq 1000000007
 6 using namespace std;
 7 long long n,m,ans,qwq;
 8 long long kuai(long long x,long long y){
 9     long long a=qaq-2;
10     long long b=1;
11     long long c=y;
12     while (a){
13         if (a&1) b=(c*b)%qaq;
14         c=(c*c)%qaq;
15         a>>=1;
16     }
17     b=(b*x)%qaq;
18     return b;
19 }
20 int main(){
21     scanf("%lld%lld",&m,&n);
22     if (n<m) swap(n,m);
23     ans=n+1;
24     qwq=n+1;
25     for (long long i=1;i<=m;i++){
26      ans=(ans+qwq)%qaq;
27      qwq=(qwq*(kuai(n+i+1,i+1)))%qaq;
28  }
29      printf("%lld\n",ans);
30 return 0;
31 }

神奇的代码

 

转载于:https://www.cnblogs.com/Lanly/p/7294701.html