【LeetCode】221. Maximal Square

最新推荐文章于 2021-11-24 21:20:25 发布

转载最新推荐文章于 2021-11-24 21:20:25 发布 · 57 阅读

本文深入探讨了Maximal Square问题的动态规划解决方案，通过构建二维数组和递推公式找到最大正方形，详细解释了算法背后的逻辑和实现过程。

Maximal Square

Given a 2D binary matrix filled with 0's and 1's, find the largest square containing all 1's and return its area.

For example, given the following matrix:

Return 4.

Credits:
Special thanks to @Freezen for adding this problem and creating all test cases.

这题的DP思想部分借鉴了jianchao.li.fighter。

思路如下：构建二维数组len，len[i][j]表示以(i,j)为右下角的最大方块的边长。

递推关系为 len[i][j] = min(min(len[i-1][j], len[i][j-1]), len[i-1][j-1]) + 1;

如下图示意：

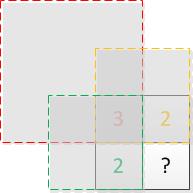
以(i,j)为右下角的最大方块边长，取决于周围三个位置(i-1,j),(i,j-1),(i-1,j-1)，恰好为三者最小边长扩展1位。

若三者最小边长为0，那么(i,j)自成边长为1的方块。

class Solution {
public:
    int maximalSquare(vector<vector<char>>& matrix) {
        if(matrix.empty() || matrix[0].empty())
            return 0;
        int m = matrix.size();
        int n = matrix[0].size();
        int maxLen = 0;
        vector<vector<int> > len(m, vector<int>(n, 0));
        // first row
        for(int i = 0; i < n; i ++)
        {
            len[0][i] = (int)(matrix[0][i]-'0');
            if(len[0][i] == 1)
                maxLen = 1;
        }
        // first col
        for(int i = 0; i < m; i ++)
        {
            len[i][0] = (int)(matrix[i][0]-'0');
            if(len[i][0] == 1)
                maxLen = 1;
        }
        for(int i = 1; i < m; i ++)
        {
            for(int j = 1; j < n; j ++)
            {
                if(matrix[i][j] == '0')
                    len[i][j] = 0;
                else
                {
                    len[i][j] = min(min(len[i-1][j], len[i][j-1]), len[i-1][j-1]) + 1;
                    maxLen = max(len[i][j], maxLen);
                }
            }
        }
        return maxLen * maxLen;
    }
};