二叉搜索树

二叉搜索树操作详解：插入与删除

最新推荐文章于 2025-09-11 21:03:21 发布

weixin_33913332

最新推荐文章于 2025-09-11 21:03:21 发布

阅读量49

点赞数

CC 4.0 BY-SA版权

文章标签： python 数据结构与算法

原文链接：https://my.oschina.net/u/1383479/blog/379978

本文深入解析二叉搜索树的基本概念、时间复杂度、遍历操作及关键算法，包括如何进行节点的插入与删除。通过具体实例与代码实现，详细阐述了这些操作的过程与细节。

2019独角兽企业重金招聘Python工程师标准>>>

性质

二叉搜索树;对于树中的每一个节点 x,x 的左子树所有节点的 key 不大于 x.key;x 的右子树的 key 不小于 x.key;如果按照 std::multimap 使用的 Compare 规则来解释,则若 x 的左子树的 key 均在 x.key 之前或之上;x 的右子树的 key 均在 x.key 之上(即位置相同)或者之后.

时间复杂度

树的高度 h 与节点个数 n 的关系;h∈[lgn(以2为底),n],这个很好推的.
遍历操作;Θ(n)
查找;前驱;后继,等其他操作;与 h 成正比,即 Θ(h).

操作算法

查找;最小值,最大值;找前驱,后继;这类不会修改二叉搜索树结构的操作算法,可以参考 libstdcxx/include/bits/stl_tree.h 中实现的红黑树.

// 变量说明;
T;表示一颗二叉搜索树,
    T.root;指针,指向着二叉搜索树的根节点.
节点;
    key;节点的键;
    parent,left,right;指针,指向着节点的父节点,孩子节点;若节点没有父节点,或者孩子节点,则置为0.
使用 < 来确定键值的先后关系;

插入

// z;指针;指向着待插入的节点.其中 z->key 为节点的键;z->parent,left,right 为 0.
insert(T,z)
    y = 0;
    x = T.root;
    insert_left = true; // 若为真,则表明 z 应该插入在 y 的左子树上.

    // 确定 z 的插入位置.
    while(x != 0)
        y = x;
        insert_left = z->key < x->key;
        x = insert_left ? x->left : x->right;
    // 当循环结束时,x==0,y 指向着 z 的父节点,而 insert_left 表明了插入位置.

    // 在 z 与 y 之间建立联系.    
    z->parent = y;
    if( y == 0)
        T.root = z;
    else
        if (insert_left)
            y->left = z;
        else
            y->right = z;

删除

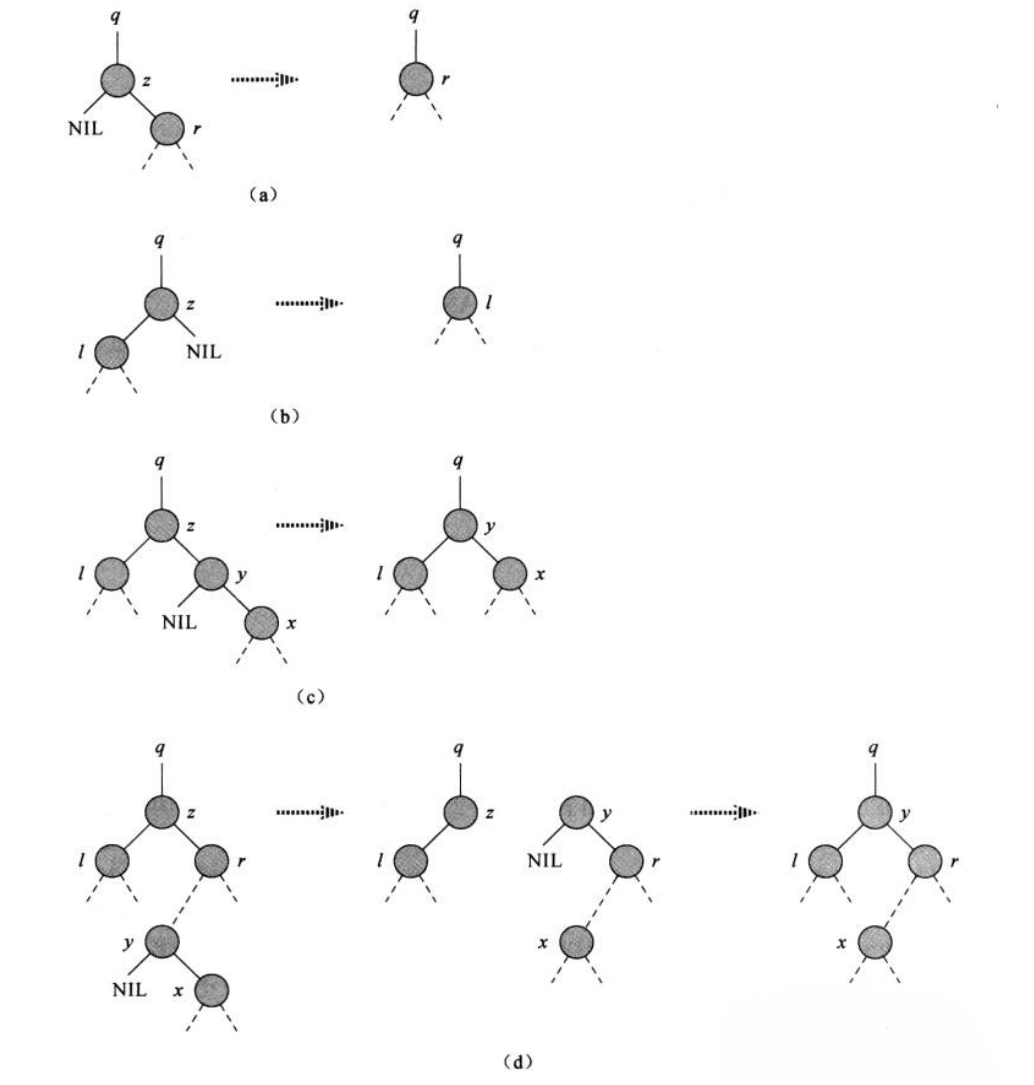
删除,可以分为4种情况来分别对待(见上图),可以从中序遍历的结果来理解,以(c)情况为例;在删除z之前,中序遍历的结果是"l左子树;l;l右子树;z;y;x左子树;x;x右子树";所以在删除 z 之后,中序遍历的结果应该是"l左子树;l;l右子树;y;x左子树;x;x右子树",也即需要对二叉搜索树做一些调整,使得调整后中序遍历结果为"l左子树;l;l右子树;y;x左子树;x;x右子树";具体调整过程见(c)左图--->右图结构.

// u,v;指针,指向着 T 中的某一节点,其中 v 可以为0.
// 该函数在 v 与 u 的父节点之间建立连接,即让 v 替代 u 成为 u 父节点的孩子节点.
traslate(T,u,v){
    up = u->parent;
    
    // up ---> v;
    if(up == 0)
        T.root = v;
    else if(up->left == u)
        up->left = v;
    else
        up->right = v;
    
    // v ---> up;
    if(v!=0)
        v->parent = up;

    // 此时;up <---> v;
}

// z;指针;指向着待删除的节点.
erase(T,z){
    // 情况 b;
    if(z->right == 0)
        translate(T,z,z->left);
    
    // 情况 a;
    else if(z->left == 0)
        translate(T,z,z->right);

    else
        y = 后继(z);
        // 情况 d 
        if(y->parent != z)
            translate(T,y,y->right);
            y->right = z->right;
            z->right->parent = y;
            // 此时情况 d 转化为 情况 c;
        // 情况 c;
        y->left = z->left;
        z->left->parent = y;
        translate(T,z,y);
}

转载于:https://my.oschina.net/u/1383479/blog/379978