谈线性变换

首先，先明确向量的基和坐标

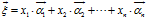
当然，也可以表示成更简洁的形式

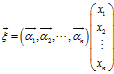，其中，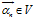

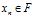
现在出现一个线性变换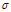，线性变换一定满足两个条件：

，

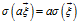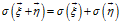
那么，线性变换能不能用个矩阵来代替呢？大部分情况是可以的。

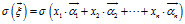
这一步仅仅是把向量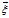用向量空间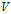的一个基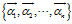来表示，因为我们已经知道线性变化满足两个很好的性质，所以对上式进行拆分

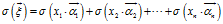
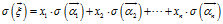，请记住这个式子，我们会回来继续推导

我们惊讶的发现，向量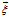被线性变换之后，可以用新的基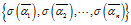表示坐标。但是，我们实在不能容忍一个向量空间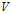用两个基来表示坐标，实在太混乱了！

既然新的基中，各个向量在向量空间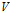内，我们一定能这样表示

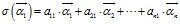
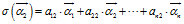
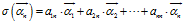
为什么坐标要取这么古怪的下标，因为我们可以用一个矩阵表示

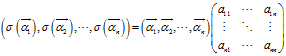
再回到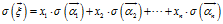

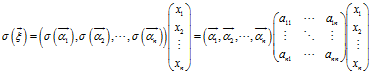
这样，我们又重新用基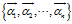来表示了，而线性变换后，坐标也就变成了

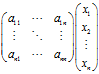
而线性变换，我们也可以用一个矩阵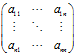来代替。

转载于:https://www.cnblogs.com/yatidashi/p/5989884.html