卡尔曼滤波简介——3.高斯分布介绍

记得Markov模型，世界被分成了离散的网络。然后给每一个网格一个固定的概率。这种表现在空间上的表现概率的方法成为直方图。他将连续的空间分成有限多的网格小块。

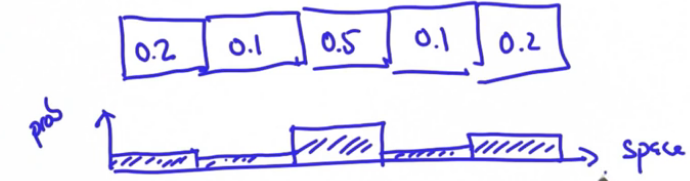
然后根据原概率分布的直方图估计后验概率的分布，这直方图仅仅对连续分布的近似表达。

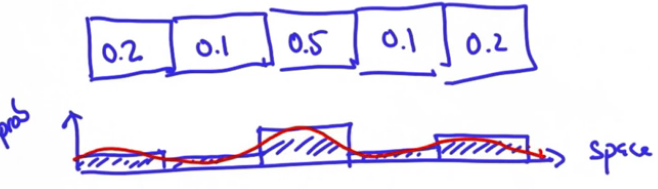
在卡尔曼滤波中 分布取决于所谓的高斯函数，高斯函数是一个空间位置的连续函数，曲线下面积为1.如果我们把这个空间成为x,那么高斯函数由两个参数来表达，一个是平均值，一个是高斯函数的宽度。

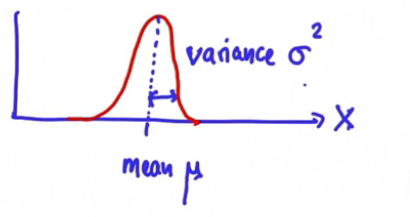
一维的高斯代表参数空间是一维的，比起用直方图估计概率分布，在卡尔曼滤波中我们的任务是保持一个对未知物体位置最佳估计的均值和方差。完整的方程是一个平方函数的指数方程。

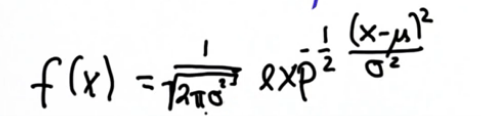
我们用一个常数对这个函数进行归一化

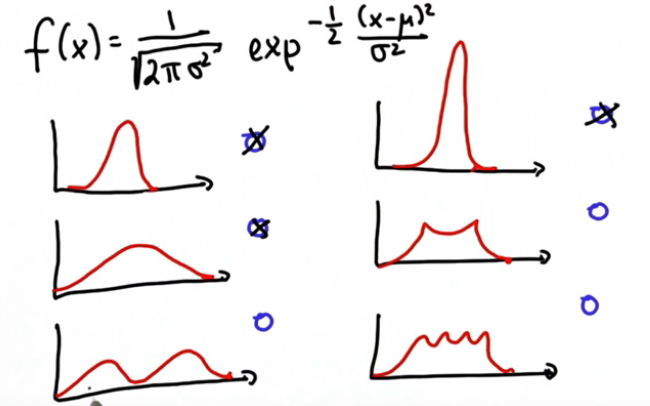
这就是所谓的单峰分布是高斯分布

 

转载于:https://www.cnblogs.com/fuhang/p/8932492.html