二叉树，二叉排序树，平衡二叉树原理及相关实现（一）-优快云博客

2019独角兽企业重金招聘Python工程师标准>>>

对于大量的输入数据，链表的线性访问时间太慢，不宜使用。树是一种在实际编程中经常遇到的数据结构，其大部分操作的运行时间平均为O(logN)。树的逻辑结构十分简单：除了根节点之外每个节点只有一个父节点，根节点没有父节点：除了叶节点之外所有节点都有一个或多个子节点，父节点和子节点之间用指针链接。

面试时提到的树大部分都是二叉树。所谓二叉树是书的一种特殊结构。在二叉树中最重要的结构莫过于遍历，即按照某一顺序访问树中的所有节点，常用的遍历方式主要有三种：前序，中序，后序。这三种遍历都有递归和循环两种不同的实现方法，每一种遍历的递归实现都比循环实现要简洁很多。

对于一颗普通的树，由于每个节点的孩子个数可以变化很大并且实现不知道，因此在数据结构中建立到各孩子节点直接的连接时不可行的，因为这样会产生太多的浪费空间。（解决方案：将每个节点的所有儿子都放在树节点的链表中。如下）

typedef struct TNode
{
 ElemType data;
 struct TNode *firstChild;
 struct TNode *NextChild;
}TreeNode, *BinaryTree;

二叉树：二叉树的一个性质是平均二叉树的深度要比N小得多。分析表明，这个平均深度为O（N^0.5），而对于特殊类型的二叉树，即二叉查找树，其平均深度为O(logN)。当然，在最坏的情况下它的深度可以达到N-1.

二叉树的主要用处之一是在编译器的设计领域。例如：表达式树：表达式树的叶子是操作数，而其他的节点是操作符，例如：

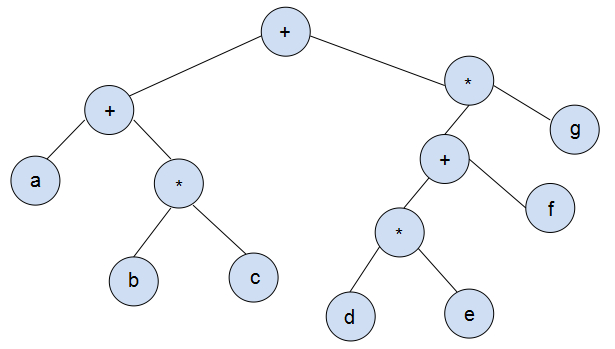
现在给出一种算法来把后缀表达式转变成表达式树。

输入：a b + c d e + * *

思路：前两个符号是操作数，因此创建两棵单节点数并将指向它们的指针压入栈中，每当读入一个操作符时，将栈顶的两个树的指针出栈，形成一个新的树，并将这棵新的树的根节点指针入栈。直至结束。

//表达式树
#include<iostream>
#include<stack>
using namespace std;

typedef char ElemType;
typedef struct TNode
{
 ElemType data;
 struct TNode *Lchild;
 struct TNode *Rchild;
}TreeNode, *BinaryTree;

TNode* ExpressionTree(char str[])
{
 stack<TNode*> s;  //创建一个栈指向二叉树的节点
 TNode *TreeNode;
 int i = 0;
 while(str[i] != '#')
 {
  if(str[i] >= 'a' && str[i] <= 'z')
  {
   TNode* childNode = new TNode();
   childNode->data = str[i];
   s.push(childNode);
  }
   
  else
  {
   TNode* treeNode = new TNode();
   treeNode->data = str[i];
   if(!s.empty())
   {
    treeNode->Rchild = s.top();
    s.pop();
   }
   else
    return treeNode;
   if(!s.empty())
   {
    treeNode->Lchild = s.top();
    s.pop();    
   }
   else
    return treeNode;
   s.push(treeNode);
   
  }
  i++;
 }
 if(s.empty())
  return NULL;
 else
 {
  TreeNode = s.top();
  return TreeNode;
 }
}

void PostOrder(BinaryTree T)  //后序遍历二叉树
{
 if(T == NULL)
  return;
 if(T->Lchild != NULL)
 {
  PostOrder(T->Lchild);
 }
 if(T->Rchild != NULL)
 {
  PostOrder(T->Rchild);
 }
 cout << T->data << " ";
}

void InOrder(BinaryTree T)    //中序遍历二叉树
{
 if(T == NULL)
  return;
 if(T->Lchild != NULL)
  InOrder(T->Lchild);
 cout << T->data << " ";
 if(T->Rchild != NULL)
  InOrder(T->Rchild);
}

int main()
{
 
 char ch[] = "ab+cde+**#";
 TNode *T;
 T = ExpressionTree(ch);
 PostOrder(T);
 cout << endl;
 InOrder(T);

 system("pause");
 return 0;
}

转载于:https://my.oschina.net/u/2260265/blog/337842